Урок №37 от 22.05.2020
Теоретическая информация:
Отбор корней можно осуществлять разными способами, самыми распространёнными являются следующие три:
1) с помощью координатной прямой;
2) с помощью неравенства;
3) с помощью тригонометрического круга.
· Оформите в тетради (перепишите или распечатайте и вложите) решение следующих заданий:
Разберём три способа отбора корней на конкретных трёх различным примерах.
Решите задания:
1) а) Решите уравнение  .
.
б) Найдите все корни этого уравнения, принадлежащие отрезку  .
.
2) а) Решите уравнение  .
.
б) Найдите все корни этого уравнения, принадлежащие промежутку  .
.
3) а) Решите уравнение  .
.
б) Найдите все корни этого уравнения, принадлежащие отрезку 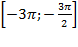 .
.
Решение:
1) а) Решите уравнение  .
.
б) Найдите все корни этого уравнения, принадлежащие отрезку  .
.
а) Решим уравнение:  ,
, 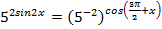 ,
, 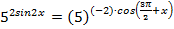 ,
,  ,
,  ;
;
Применим формулу приведения:  и перепишем уравнение:
и перепишем уравнение:  ,
,
 ,
,  ;
;
Применим формулу синуса двойного угла  и перепишем уравнение:
и перепишем уравнение: 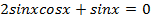 ;
;
Вынесем  за скобки:
за скобки: 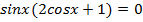 ,
,
 или
или  ;
;
1) 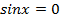 , данное уравнение можно решить с помощью тригонометрического круга (синус соответствует оси
, данное уравнение можно решить с помощью тригонометрического круга (синус соответствует оси  ,
,  в точке
в точке  и
и 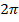 ),
), 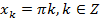 ,
,
2)  ,
,  ,
,  ;
;
 и
и  ,
,
 и
и  ,
,
 и
и  ,
,
 и
и 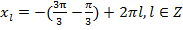 ,
,
 и
и  .
.
б) Произведём отбор корней с помощью координатной оси:
1) 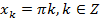 ,
,


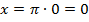 ,
,
данный корень находится левее промежутка, то есть вне промежутка, поэтому 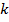 нужно брать больше 0,
нужно брать больше 0,
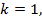
 ,
,
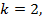
 ,
,

 ,
,
данный корень совпадает с правым концом промежутка, поэтому если 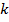 брать больше 3, корни будут находиться правее промежутка, то есть вне промежутка.
брать больше 3, корни будут находиться правее промежутка, то есть вне промежутка.
В результате внутри промежутка оказались два корня 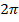 и
и 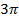 .
.
2)  ,
,


 ,
,
данный корень находится левее промежутка, то есть вне промежутка, поэтому  нужно брать больше 0,
нужно брать больше 0,
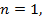
 ,
,

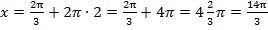 ,
,
данный корень находится правее промежутка, то есть вне промежутка, поэтому если 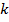 брать больше 2, корни будут находиться также правее промежутка, то есть вне промежутка.
брать больше 2, корни будут находиться также правее промежутка, то есть вне промежутка.
В результате внутри промежутка оказался один корень 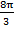 .
.
3)  ,
,


 ,
,
данный корень находится левее промежутка, то есть вне промежутка, поэтому  нужно брать больше 0,
нужно брать больше 0,
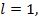
 ,
,
данный корень находится левее промежутка, то есть вне промежутка, поэтому  нужно брать больше 1,
нужно брать больше 1,

 ,
,
данный корень находится правее промежутка, то есть вне промежутка, поэтому если  брать больше 2, корни будут находиться также правее промежутка, то есть вне промежутка.
брать больше 2, корни будут находиться также правее промежутка, то есть вне промежутка.
В результате внутри промежутка не оказалось ни одного корня.
Ответ: а) 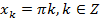 ,
,  ,
,  .
.
б) 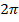 ,
, 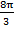 ,
, 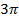 .
.
2) а) Решите уравнение  .
.
б) Найдите все корни этого уравнения, принадлежащие промежутку  .
.
а) Решим уравнение:  ,
,
Применим формулу приведения  и перепишем уравнение:
и перепишем уравнение:  ,
,  ,
, 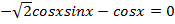 ,
,
 ,
,
Вынесем  за скобки:
за скобки:  ,
,
 или
или 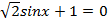 ,
,
1)  , данное уравнение можно решить с помощью тригонометрического круга (косинус соответствует оси
, данное уравнение можно решить с помощью тригонометрического круга (косинус соответствует оси  ,
, 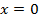 в точке
в точке  и
и 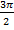 ),
), 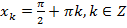 ,
,
2) 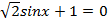 ,
, 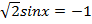 ,
, 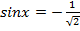 ,
,  ,
,
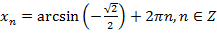 и
и 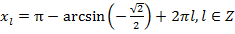 ,
,
 и
и  ,
,
 и
и  ,
,
 и
и  ,
,
 и
и  .
.
б) Произведём отбор корней с помощью неравенства:
 ;
;
 ,
,
 ,
,
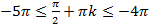 ,
, 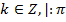
 ,
, 
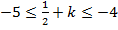 ,
, 
 ,
, 
 ,
, 
 ,
, 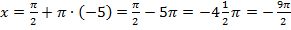 .
.
 ,
,
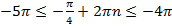 ,
, 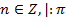
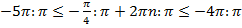 ,
, 
 ,
, 

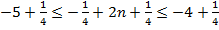 ,
, 
 ,
, 
 ,
, 
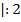
 ,
, 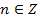 ,
,
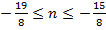 ,
, 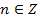
 ,
, 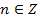
 ,
, 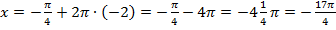 .
.
3)  ,
,
 ,
, 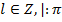
 ,
, 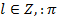
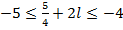 ,
, 
 ,
, 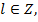
 ,
, 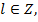
 ,
, 
 ,
, 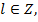
 ,
, 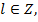
 ,
, 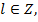
 ,
,  .
.
Ответ: а) 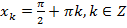 ,
,  ,
,  .
.
б)  ,
,  ,
, 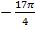 .
.
3) а) Решите уравнение  .
.
б) Найдите все корни этого уравнения, принадлежащие отрезку 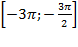 .
.
а) Решим уравнение: 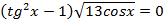 ,
,
Найдем область определения данного уравнения:
Заметим, что первый множитель содержит тангенс, поэтому  , а второй множитель содержит корень, поэтому
, а второй множитель содержит корень, поэтому  ,
,  . Вместе имеем
. Вместе имеем  .
.
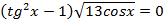 ,
,
 или
или 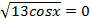 ,
,
1)  ,
,  ,
, 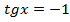 или
или 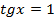 ;
;
 ,
, 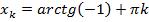 ,
, 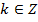 ,
, 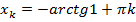 ,
, 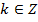 ,
,  ;
;
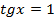 ,
, 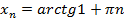 ,
, 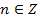 ,
,  ;
;
2) 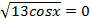 ,
,  ,
,  , данное уравнение можно решить с помощью тригонометрического круга (косинус соответствует оси
, данное уравнение можно решить с помощью тригонометрического круга (косинус соответствует оси  ,
, 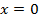 в точке
в точке  и
и 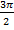 ),
),
 .
.
С учётом области определения имеем  и
и 
б) Произведём отбор корней с помощью тригонометрического круга
 ,
,
1)  ,
,

 ,
,
данный корень находится вне промежутка, поэтому 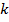 нужно брать меньше 0,
нужно брать меньше 0,
 ,
, 
 ,
, 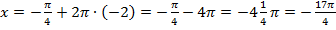
данный корень находится вне промежутка, поэтому если 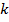 брать меньше
брать меньше  , корни будут находиться также вне промежутка.
, корни будут находиться также вне промежутка.
В результате внутри промежутка оказался один корень  .
.
2)  ,
,

 ,
,
данный корень находится вне промежутка, поэтому  нужно брать меньше 0,
нужно брать меньше 0,
 ,
, 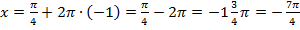
 ,
, 
данный корень находится вне промежутка, поэтому если  брать меньше
брать меньше  , корни будут находиться также вне промежутка.
, корни будут находиться также вне промежутка.
В результате внутри промежутка оказался один корень  .
.
Покажем оба корня на чертеже:

Ответ: а)  ,
,  .
.
б)  ,
,  .
.
· Выполнить домашнее задание на карточке
Карточка
Некоторое тригонометрическое уравнение имеет корни  ,
,  ,
, 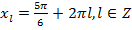 . Любым из трёх способов произведите отбор корней, принадлежащих следующим промежуткам:
. Любым из трёх способов произведите отбор корней, принадлежащих следующим промежуткам:
1) 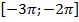 , 2)
, 2)  , 3)
, 3) 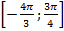 .
.
· Домашнее задания оформите в тетради.
· Сфотографируйте в разборчивом виде.
· Передайте мне до 25.05.2020 через эл.дненик, Whatsapp, или VK.
Критерии оценивания заданий карточки
Каждый верно отобранный набор корней для каждого промежутка – 1 балл.
Баллы суммируются. Максимальное количество баллов – 9.
Перевод баллов в оценки
9 баллов – оценка «5»
7-8 баллов – оценка «4»
5-6 баллов – оценка «3»
менее 5 баллов – оценка «2»
 2020-07-12
2020-07-12 121
121






