Сведение показательного неравенства к системе рациональных неравенств

       Рассмотрим показательное неравенство вида

             (3)

где  - некоторые функции.

Традиционное решение такого неравенства приводит к двум случаям:

1. если 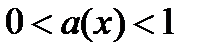, то ;          2.если , то .

       Как и в случае с логарифмическим неравенством, имеется возможность значительно укоротить решение задачи, используя метод рационализации. Этот метод основан на следующей теореме.

Теорема 2. Показательное неравенство

равносильно следующей системе неравенств:

  (4)

Нетрудно заметить, что система (4) аналогична системе (2) из теоремы 1 (правда, в ней нет требования положительности степеней). 

Пример 2. Решить неравенство

.

Решение. Составим систему неравенств, аналогичную системе (4) из теоремы 2:

Решив два первых неравенства, найдем ОДЗ исходного показательного неравенства:

Откуда ОДЗ: .

Далее рассмотрим основное неравенство , которое приводится  к виду: .

Корни первого множителя этого неравенства мы нашли ранее: . Корни второго множителя равны: , , .

Так как , то . Применив метод интервалов, получим следующее решение основного неравенства: .

Учитывая найденную ранее ОДЗ, получаем окончательный ответ:

.

Пимер 3. Решить систему неравенств

 

Решение:  Рассмотрим решение каждого неравенства отдельно:

 

(2): введем замену

- система несовместна, т.к. по первому неравенству

 Выберем решение системы , т.к. .

Ответ: .

 

 

Задания для самостоятельного решения.

1.

2.

3.

4.

5.

6.

 

.