Тема. Значения и свойства синуса, косинуса,
Тангенса и котангенса угла
Вопросы темы:
Значения синуса, косинуса тангенса и котангенса угла.
Свойства синуса, косинуса, тангенса и котангенса угла
Вопрос 1 Значения синуса, косинуса тангенса и котангенса угла
Повторим соотношение сторон прямоугольного треугольника АВС
Катеты BC и AC прямоугольного треугольника ABC (рис. 1) называют противолежащим катетом угла α и прилежащим катетом угла α соответственно.
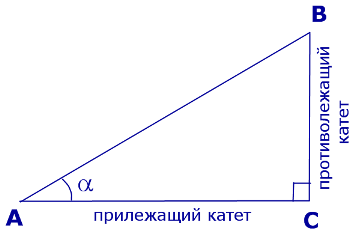
Рис.1
Катеты AC и BC прямоугольного треугольника ABC (рис. 2) называют противолежащим катетом угла β и прилежащим катетом угла β соответственно.
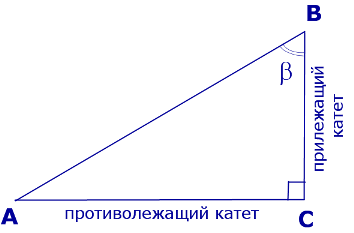
Рис.2
Синусом угла называют дробь: 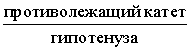
Косинусом угла называют дробь: 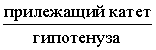
Тангенсом угла называют дробь: 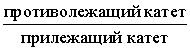
Котангенсом угла называют дробь: 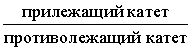
Для синуса, косинуса, тангенса и котангенса угла α используют обозначения:
sin α, cos α, tg α, ctg α
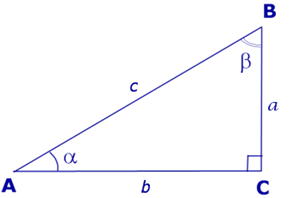
Рис.3
В соответствии с рисунком 3 справедливы формулы:
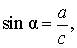
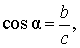
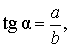
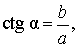
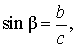
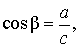
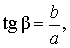
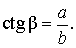
Следовательно,
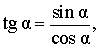
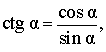
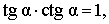
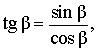
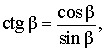
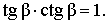
Кроме того, справедливы формулы:
sinα = cos β, cosα = sinβ, tgα = ctgβ, ctgα = tgβ,
которые можно переписать в виде:
sinα = cos(90 – α), cosα = sin(90 – α),
tgα = ctg(90 – α), ctgα = tg(90 – α).
Пример. Найти тригонометрические функции углов 30°, 45°, 60°.
Решение.
Рассмотрим равносторонний треугольник ABC, сторона которого равна 2 (рис. 4), и проведем высоту BD.
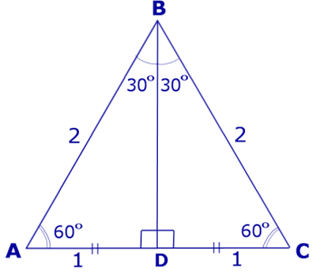
Рис.4
Тогда
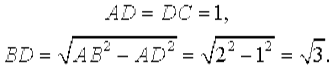
Поэтому
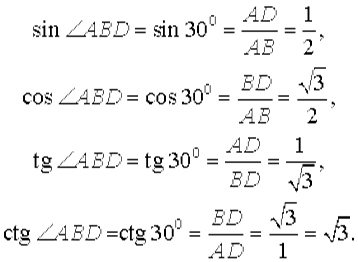
Кроме того
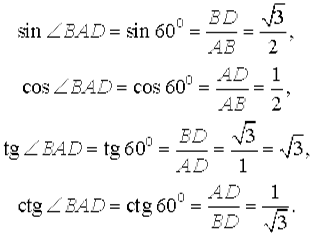
Теперь рассмотрим прямоугольный равнобедренный треугольник ABC, катеты которого равны 1 (рис. 5).
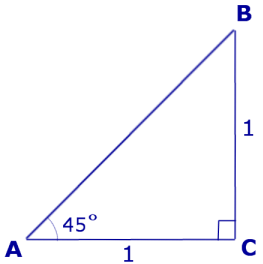
Рис.5
Тогда
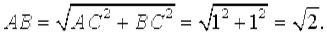
Поэтому
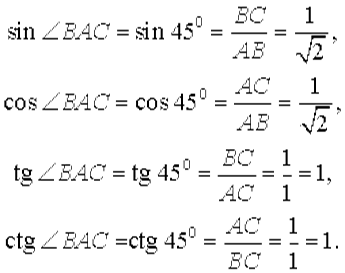
Вычисленные значения синуса, косинуса, тангенса и котангенса угла прямоугольного треугольника можно рассмотреть и с помощью известной нам единичной окружностью, на которой можно найти значения синуса, косинуса, тангенса и котангенса соответствующих табличных углов поворота (Рис.6).
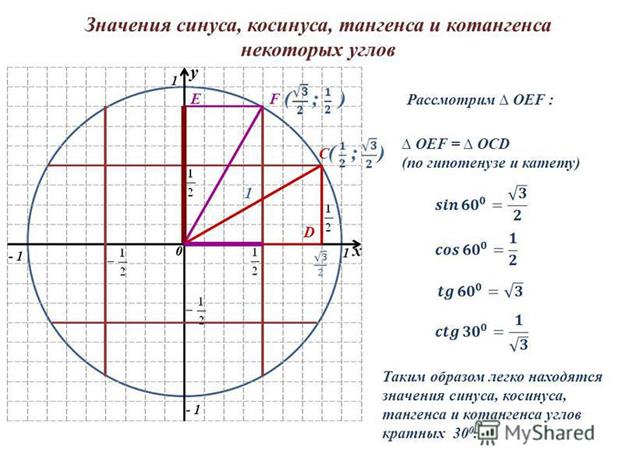
Рис.6
Полученные значения синуса, косинуса, тангенса и котангенса табличных углов поворота внесем в Таблицу.
Таблица значений тригонометрических функций
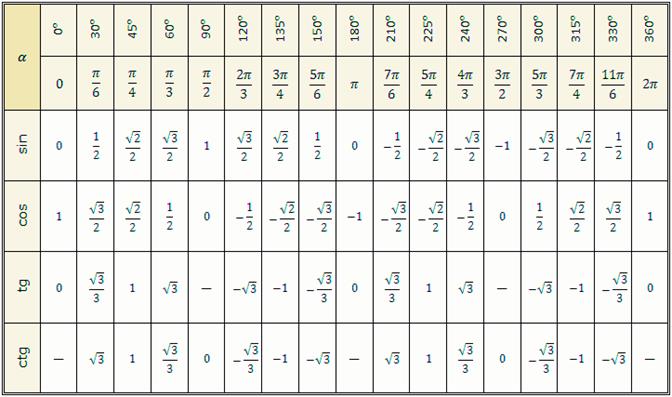
Вопрос 2
Определения синуса, косинуса, тангенса и котангенса угла позволяют установить ряд характерных свойств синуса, косинуса, тангенса и котангенса.
Рассмотрим эти три основных свойства.
Первое свойство указывает – знаки синуса, косинуса, тангенса и котангенса угла α – в зависимости от того, углом какой координатной четверти является α.
Второе свойство – периодичности, устанавливающее неизменность значений синуса, косинуса, тангенса и котангенса угла α при изменении этого угла на целое число оборотов.
Третье свойство – выражает зависимость между значениями синуса, косинуса, тангенса и котангенса противоположных углов α и −α.
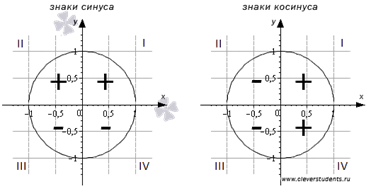
Свойство 1
Знаки синуса, косинуса, тангенса и котангенса по четвертям
Объясним фразу: «угол I, II, III и IV координатной четверти». Что это за углы.
Возьмем единичную окружность:
- отметим на ней начальную точку А(1, 0),
- повернем ее вокруг точки O на угол α, при этом будем считать, что мы попадем в точку A1(x, y).
Говорим (считаем), что:
- угол α является углом I, II, III, IV координатной четверти, если точка А1 лежит в I, II, III, IV четверти соответственно;
- если угол α таков, что точка A1 лежит на любой из координатных прямых Ox или Oy, то этот угол не принадлежит ни одной из четырех четвертей.
Пример:
Углы поворота 30°, -210°, 585° и -45° – являются углами I, II, III и IV координатных четвертей соответственно.
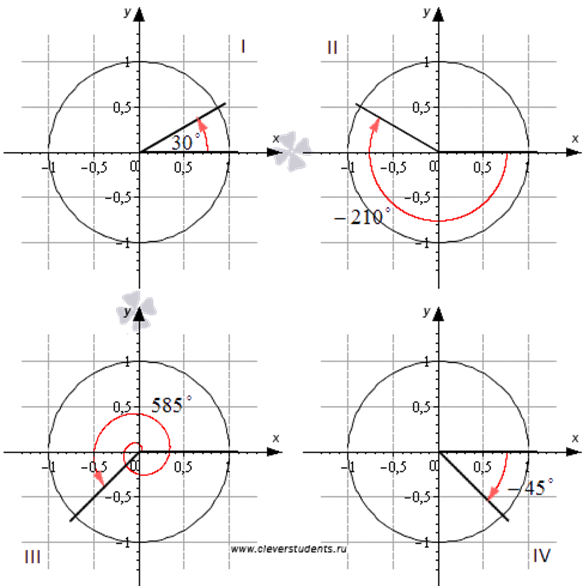
Углы 0°, ±90°, ±180°, ±270°, ±360°, … не принадлежат ни одной из координатных четвертей.
Определим, какие знаки имеют значения синуса, косинуса, тангенса и котангенса угла поворота α в зависимости от того, углом какой четверти является α.
1. Для синуса и косинуса
1.1. По определению:
Синус угла α – это у – ордината точки А1
В I и II координатных четвертях она положительна.
В III и IV четвертях – отрицательна.
Таким образом, синус углаα имеет:
- знак плюс - в I и II четвертях,
- знак минус – в III и VI четвертях.
1.2. По определению:
Косинус угла α – это х – абсцисса точкиA1
В I и IV четвертях она положительна.
Во II и III четвертях – отрицательна.
Следовательно, значения косинуса угла α имеют
- знак плюс - в I и IV четвертях,
- знак минус – во II и III четвертях.
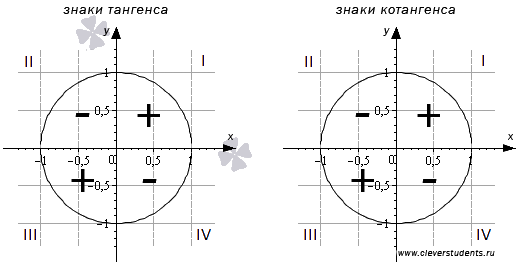
2. Для тангенса и котангенса
Чтобы определить знаки по четвертям тангенса и котангенса нужно вспомнить их определения:
тангенс угла α – это отношение ординаты точки A1 к абсциссе - х/у;
котангенс угла α – это отношение абсциссы точки A1 к ординате - у/х.
Тогда из правил деления чисел с одинаковыми и разными знаками следует, что тангенс и котангенс имеют:
- знак плюс, когда знаки абсциссы и ординаты точки A1 одинаковые,
- знак минус – когда знаки абсциссы и ординаты точки A1 различны.
Следовательно, тангенс и котангенс угла имеют:
- знак плюс в I и III координатных четвертях,
- знак минус – во II и IV координатныхчетвертях.
Действительно:
- в первой четверти и абсцисса x, и ордината y точки A1 положительны, тогда и частное x/y, и частное y/x – положительно, следовательно, тангенс и котангенс имеют знаки плю с;
- во второй четверти абсцисса x – отрицательна, а ордината y – положительна, поэтому и x/y, и y/x – отрицательны, следовательно, тангенс и котангенс имеют знаки минус.
Ниже рассмотрим следующее, второе, свойство синуса, косинуса, тангенса и котангенса.
Свойство 2
Свойство периодичности
Это самое очевидное свойство синуса, косинуса, тангенса и котангенса угла.
Свойство периодичности состоит в следующем:
при изменении угла на целое число полных, соответствующих для данной функции, оборотов значения синуса, косинуса, тангенса и котангенса этого угла не изменяются.
Доказательство: при изменении угла на целое число соответствующих для данной функции оборотов (для синуса и косинуса – это полный оборот, для тангенса и котангенса – половинный оборот) мы из начальной точки А всегда будем попадать в точку А1 на единичной окружности, следовательно, значения синуса, косинуса, тангенса и котангенса остаются неизменными, так как неизменны координаты точки A1.
С помощью формул рассматриваемое свойство синуса, косинуса, тангенса и котангенса можно записать так:
sin(α+2·π·z) = sinα cos(α+2·π·z) = cosα
tg(α+·π·z)= tgα ctg(α+·π·z) = ctgα
где α - угол поворота в радианах,
z – любое целое число, абсолютная величина которого указывает количество полных оборотов, на которые изменяется угол α, а знак числа z указывает направление поворота.
Если угол поворота α задан в градусах, то указанные формулы перепишутся в виде:
sin(α+360°·z) = sinα cos(α+360°·z) = cosα
tg(α+360°·z) = tgα ctg(α+360°·z) = ctgα
Примеры использования этого свойства.
1.
 , так как
, так как  , а
, а 
2. 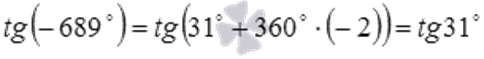
3. 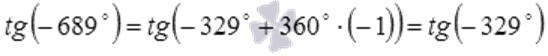
Это свойство часто используется при вычислении значений синуса, косинуса, тангенса и котангенса «больших» углов (больше, чем острый угол).
Итак, рассмотренное свойство синуса, косинуса, тангенса и котангенса называют свойством периодичности.
Свойство 3
Свойства синусов, косинусов, тангенсов и котангенсов противоположных углов.
Пусть:
- точка А1 – это результат поворота начальной точки А(1; 0) вокруг точки O на угол α,
- точка А2 – это результат поворота точки А(1; 0) на угол - α, противоположный углу α.

Свойство синусов, косинусов, тангенсов и котангенсов противоположных углов - базируется на достаточно очевидном факте:
точки А1 и А2: 1) либо совпадают (при 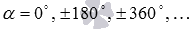 ),
),
2)– либо располагаются симметрично
относительно оси Ox.
То есть,
- если точка A1 имеет координаты (x; y), то
- точка А2 будет иметь координаты (x; −y).
Отсюда,исходя из определений синуса, косинуса, тангенса и котангенса, можем записать следующие равенства:

и
sin(-a) = -у cos(-a) = х tg(-a) = -у/х ctg(-a) = х/-у
Сопоставляя их, приходим к соотношениям между синусами, косинусами, тангенсами и котангенсами противоположных углов α и -α, которые можно записать в следующем виде:
sin(-a) = - sin a cos(-a) = cos a
tg(-a) = -tg a ctg(-a) = -ctg a
Выше указанные формулы представляют данное свойство в аналитическом виде, то есть в виде формулы.
Примеры использования данного свойства:
1. Справедливы равенства:
 ,
, 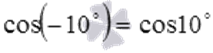
Свойство синусов, косинусов, тангенсов и котангенсов противоположных углов, как и предыдущее свойство, часто используется при вычислении значений синуса, косинуса, тангенса и котангенса, и позволяет полностью уйти от отрицательных углов.
Домашнее задание:
1. В тетради по математике сделать конспект по данной теме.
2. Выучить законспектированный материал.
3. Выучить и знать перечисленные в данном материале свойства синуса, косинуса, тангенса и котангенса угла.
4. Выучить и знать значения синуса, косинуса, тангенса и котангенса угла (таблица).
 2020-07-12
2020-07-12 196
196






