Тема посвящена обобщению и систематизации имеющихся знаний по теме «Тригонометрические функции и их свойства». А всякое знание должно перейти в умение и навык. Проверим свои знания, умения и навыки, выясним пробелы и попытаемся их ликвидировать. Мы сегодня вспомним, как определять значение функции по значению аргумента при различных способах задания функции; строить графики изученных функций; описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения.
1. Актуализация опорных знаний.
Работа по карточкам
| Вариант №1 | Вариант №2 |
1. Постройте график функции 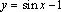 ; 2. Укажите область значений данной функции; 3. Найдите наибольшее и наименьшее значения функции на интервале ; 2. Укажите область значений данной функции; 3. Найдите наибольшее и наименьшее значения функции на интервале 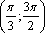
| 1. Постройте график функции 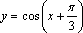 ; 2. Укажите промежутки возрастания и убывания функции; 3. Определите нули функции. ; 2. Укажите промежутки возрастания и убывания функции; 3. Определите нули функции.
|
Проверяем и сравниваем функции.
Какие свойства тригонометрических функций вы использовали при решении заданий?
| 1 вариант: y=sinx, Область определения Точки пересечения с осями координат Четность и нечетность Промежутки монотонности Экстремумы Периодичность Промежутки знакопостоянства Множество значений | 2 вариант:y=cos x, Область определения Точки пересечения с осями координат Четность и нечетность Промежутки монотонности Экстремумы Периодичность Промежутки знакопостоянства Множество значений |
1. Практикум по решению задач
1. В одной системе координат построить графики функций одной группы и описать их свойства:
1) 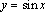 ,
, 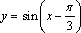 . 2)
. 2) 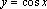 ,
, 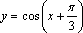 .
.
Обобщить преобразования графиков функций сдвигом по оси 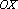 .
.
В одной системе координат построить графики функций одной группы и описать их свойства:
1) 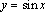 ,
, 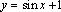 . 2)
. 2) 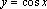 ,
, 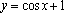 .
.
2. Докажите, что число 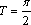 является периодом функции
является периодом функции 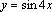 .
.
3. Докажите, что число 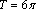 является периодом функции
является периодом функции 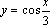 .
.
4. Найдите наименьший положительный период функции 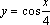
5. Найдите наименьший положительный период функции 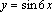
6. Переведите из градусной меры в радианную и расположите в порядке возрастания: 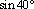 ,
, 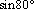 ,
, 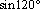 ,
, 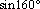 .
.
7. Переведите из радианной меры в градусную и расположите в порядке убывания: 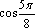
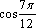 ,
, 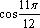 ,
, 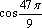 .
.
1. Повторить свойства тангенса и котангенса.
2. Ответы отправить на почту mathetuka@yandex.ru
 2020-08-05
2020-08-05 55
55






