Урок геометрии 7 класс.
| Цель | Создать условия для повторения основных задач на построение; совершенствовать навыки решения задач на построение |
| Актуализация опорных знаний учащихся | |
| 1. Повторите как (п. 38-39) 1) на данном луче от его начала отложить отрезок, равный данному; 2) отложить от данного луча угол, равный данному; 3) построить биссектрису данного неразвернутого угла; 4) построить прямую, проходящую через данную точку и перпендикулярную к прямой, на которой лежит данная точка; 5) построить середину данного отрезка; 6) построить прямую, проходящую через данную точку и перпендикулярную к прямой, не проходящей через данную точку. 7) Построить треугольник: 1) по двум сторонам и углу между ними; 2) по стороне и прилежащим к ней углам; 3) по трем сторонам | |
| Решение задач. Посмотрите решение и запомните. | |
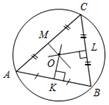
| № 353. Анализ (см. рис.1): Рис. 1 Пусть X – искомая точка, то есть АХ = ХВ, тогда ∆ АХВ – равнобедренный и XY – медиана, высота и биссектриса. Отсюда получаем план построения. План построения: 1) Построить точку Y – середину АВ. 2) Построить прямую, проходящую через Y и перпендикулярную АВ. 3) Прямая b пересекается с окружностью в точках Х и Z. Х и Z – искомые точки. Построение (см. рис. 2):
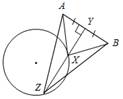
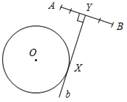
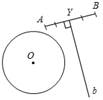
Рис. 2 Доказательство: ∆ AYX = ∆ BYX по двум катетам (они прямоугольные, так как Исследование: Задача может иметь: а) два решения (см. план построения и построение); б) одно решение, если прямая b имеет одну общую точку с окружностью (касается ее) (рис. 3); в) ни одного решения, если прямая b не имеет общих точек с окружностью (рис. 4).
Рис. 3 Рис. 4 № 354. Соединяем точки А, В и С. Находим середины отрезков АВ, ВС и АС, соответственно K, L и М. Проводим перпендикуляры (серединные перпендикуляры D АВС). Вокруг треугольника всегда можно описывать окружность, поэтому задача не имеет решения, лишь когда точки лежат на одной прямой.
Рис. 5 № 360.
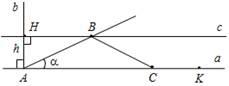
Рис. 6 Проводим прямую а. Отмечаем на ней точку А – одну из вершин нашего треугольника, на прямой откладываем отрезок, равный периметру треугольника. На прямой b откладываем отрезок АН, равный высоте треугольника. Строим заданный Ða с вершиной в точке А. Проводим прямую с ^ b, Н ^ с. Обозначим точку пересечения с со стороной Ða – В. От точки K откладываем на прямой а отрезок, равный АВ – KC. Соединяем В и С. АВС – искомый треугольник. № 362.
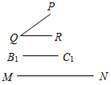
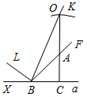
а) Рис. 7 б) Пусть надо построить D АВС, и даны Ð PQR и отрезки В 1 С 1, равный стороне треугольника, и MN, равный сумме двух других сторон треугольника (см. рис. а). Проведем произвольную прямую а, отметим на ней точку В и точку Х (см. рис. б). Ð KAB = Ð АВС + Ð АСВ (как внешний). D KAB – равнобедренный (так как Ð BKA = Ð KBA по построению). Значит, Ð KBA = Ð KBС = Ð KBA + Ð АВС =
Ð LBC = 2Ð KBС = 180° + Ð АВС – Ð АСВ (так как BK – биссектриса угла LBC). Ð PQR = Ð XBL = 180° – Ð LBC = 180° – 180° – Ð АВС + Ð АСВ = Ð АСВ – Ð АВС. АВ = AK, так как D KBA – равнобедренный, значит, MN = KA + АС = АВ + АС, | |
 2020-08-05
2020-08-05 430
430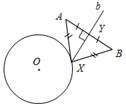
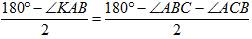 .
.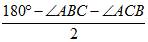 + Ð АВС =
+ Ð АВС =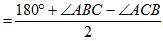 .
.






