Преподаватель: Пронина Е.А

Дисциплина: Математика

Занятие 107. Решение задач с помощью комбинаторных формул.

План занятия:

1. Повторение: размещения, сочетания, перестановки.

2. Примеры решения комбинаторных задач.

3. Задачи для самоконтроля.

Видео-материалы:  https://www.youtube.com/watch?v=SLPrGWQBX0I

Размещениями из n элементов по k элементов называются наборы k элементов, отличающиеся один от другого или самими элементами (составом элементов), или их порядком. Число размещений обозначается A .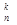

Число размещений из n элементов по k элементов находится по формуле:

А 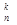=n∙(n–1)∙(n–2)∙…∙(n–(k–1))       

Перестановками из данных n элементов называются наборы из n элементов, различающихся только порядком.

Р 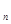=1·2·3 …∙n=n!

      Сочетаниями, содержащими k элементов, выбранных из n элементов заданного множества, называются всевозможные наборы k элементов, различающиеся хотя бы одним элементом. Число сочетаний из n элементов по k элементов обозначают С .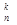

Число сочетаний из n элементов по k элементов определяется формулой:

С =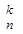

Пример 1. Определить, сколько трехзначных чисел можно составить из множества цифр 7,8,9,3,2 без повторений.

Решение. Трехзначные числа можно рассматривать как размещения, так как при замене одной цифры другой или перестановке их местами получаются разные числа. Так как n=5, k=3, то различных чисел будет:

А 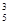 =5·4·3=60.

Пример 2. К кассе за получением (или для уплаты) денег подошли одновременно 4 человека. Сколькими способами они могут выстроиться в очередь?

Решение. Очередь состоит из 4 различных лиц, поэтому в каждом способе составления очереди учитывается порядок их расположения. Таким образом, имеют место перестановки из четырёх человек, их число равно:

Р₄ = 4! = 24.

Пример 3. В цехе 18 человек, из них 10 мужчин. На конференцию отбирают 6 человек так, что было 3 мужчины и 3 женщины. Сколько различных списков можно составить?

Решение. 3-х мужчин из 10 человек можно отобрать С различными способами, 3-х женщин из 8 можно отобрать С 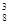различными способами. Следовательно, 3-х женщин и 3-х мужчин можно отобрать С  · С 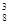– различными способами.

Найдем: С = = ,

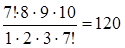С = = .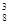

Итого, число различных списков:

С  ∙ С 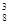= 120 · 54 = 6480.

Пример 4. В урне 10 красных и 7 зеленых шаров, достаем 1 шар. Рассмотрим события: А – из урны вынут красный шар, В – из урны вынут зеленый шар. Найдём вероятности этих событий.

Решение. Всего в урне 17 шаров, тогда n = 17. Благоприятствующими исходами для события А будет извлечение любого из 10 красных шаров, то есть m = 10, таким образом Р(А) = .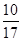

Аналогично Р(В) = .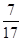

Пример 5.  На конференцию из группы студентов из 20 человек (8 девушек, 12 юношей) отбирают 5 человек. Найти вероятность следующих событий:

А – среди отобранных студентов одни юноши,

В – среди отобранных студентов одни девушки,

С – среди отобранных 2 девушки и 3 юношей. 

Решение. Заметим, что общее число исходов для всех трех событий будет одинаковым n= C .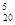

Число благоприятствующих исходов: m_А = C 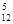, m_В = C 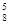, m_С = C 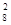∙С .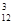

Следовательно, получаем вероятность появления события А:

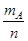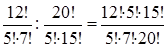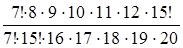
Р(А)= =  = = = 0,051.

Найдем вероятность появления события В:

Р(В)= = = = = 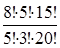=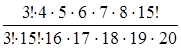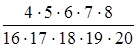0,006

Аналогично получаем:

Р(С)= 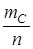= = 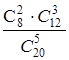= = = 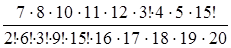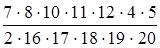0,0795.

 

Заметим, что вероятность достоверного события равна 1, а вероятность невозможного равна 0. Вероятность случайного события А заключена между 0 и 1. Итак, для любого события верно неравенство: 0 ≤ Р(А) ≤ 1.