РАЗДЕЛ 12. УРАВНЕНИЯ И НЕРАВЕНСТВА
ТЕМА: Показательные уравнения
Цель занятия: научиться решать показательные уравнения.
Порядок выполнения работы:
1) Изучить теоритический материал, составить краткий конспект в тетради;
2) В течение пары выполнить задания по материалу лекции (решить в тетради и выслать фотографии или документ преподавателю в социальной сети или на личную почту);
Контакты преподавателя: Arina_Kozlova96@mail.ru; https://vk.com/rina1996
ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ ДЛЯ САМОСТОЯТЕЛЬНОГО ИЗУЧЕНИЯ
Показательное уравнение – это уравнение c переменной в показателе степени.
Примеры:
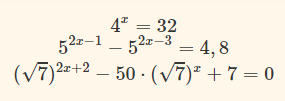
Существует два типа показательных уравнений:
· 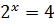 – показательное уравнение с иксом в степени;
– показательное уравнение с иксом в степени;
· 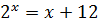 – смешанное, ведь икс находится также и в основании.
– смешанное, ведь икс находится также и в основании.
При этом:
· 2 – основание, оно должно соответствовать двум условиям, а именно: быть больше нуля и отличаться от единицы;
· х – показатель.
Для решения уравнений такого вида необходимо опираться на свойства степеней:
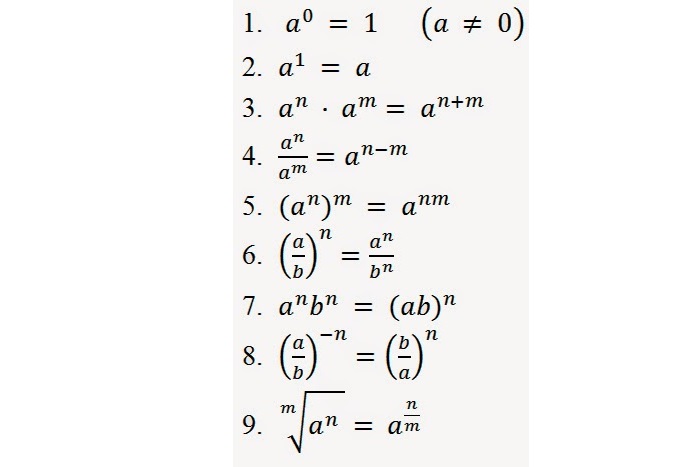
| Свойства степеней |
Как решать показательные уравнения

Например: 
Важно! Из той же логики следуют два требования для такого перехода:
· число в основании степени слева и справа должно быть одинаковым;
· степени слева и справа должны быть «чистыми», то есть не должно быть никаких коэффициентов, умножений, делений и т.д.
Например:

Примеры решения показательных уравнений
ПРИМЕР 1. Упростить и решить уравнение 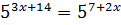
В обеих частях примера одинаковые основания, значит, можно приравнять математические выражения, находящиеся в показателе. В результате получится: 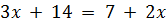 .
.
Путем переноса чисел в одну часть, а переменных в другую, не сложно решить пример. Главное, не забывать менять знак на противоположный, плюс на минус и наоборот:
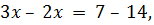
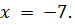
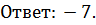
ПРИМЕР 2. Выполнить вычисление и найти x:
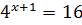 ,
,
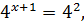
Основания обеих частей примера – 4, оно не меняется, следовательно, можно воспользоваться изученными свойствами и получить простейшее уравнение:
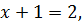
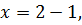
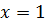
Ответ: 1
Рассмотрим еще несколько подобных примеров:

ПРИМЕР 3. Упростить и найти значение х:
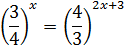
Дроби в примере разные. Поэтому приравнять их показатели сразу не получится. Но стоит обратить внимание, что числитель одной равен знаменателю другой и наоборот.
Чтобы решить, придется вспомнить о правиле возведения в отрицательную степень, когда выражение представляется в виде дроби. Значит, числитель можно поменять местами со знаменателем.
В показателе при этом появится знак «минус»:
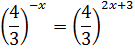
При равных основаниях приравниваются степени: 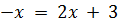 .
.
Далее придется выполнить простое действие, чтобы найти неизвестную переменную:
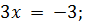
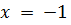
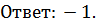
ПРИМЕР 4. Вычислить: 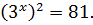
Можно представить в следующем виде: 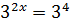 .
.
Далее выполнить простые действия, чтобы получить результат: 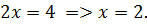
Ответ: 2.
ПРИМЕР 5.
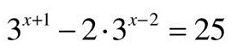
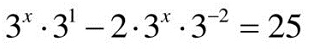
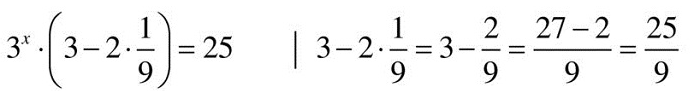
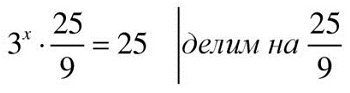
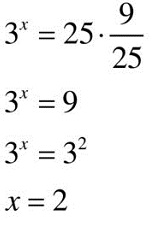
Ответ: 2.
ПРИМЕР 6. Решить уравнение: 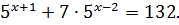
Если воспользоваться свойством степеней, применяемых для умножения значений с одинаковым основанием, можно преобразовать уравнение. Общий множитель, прежде всего, нужно поставить за скобки, это правило регулярно применяется при решении:
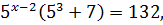
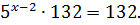
Если обе части уравнения разделить или умножить на одно и то же число, результат не изменится. В данном случае необходимо разделить на число 132. Это помогает избавиться от громоздких вычислений, удлиняющих ход решения:
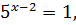
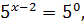

Остается только приравнять показатели и решить элементарный пример:
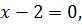
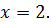
Ответ: 2.
ПРИМЕР 7. Решить показательное уравнение: 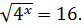
Квадратный корень можно заменить степенью 1/2.
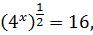
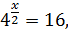
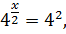
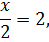
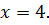
Ответ: 4.
ПРАКТИЧЕСКИЕ ЗАДАНИЯ
Решить показательные уравнения:
1) 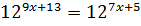
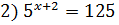
3) 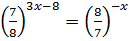
4) 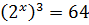
5) 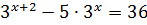
6) 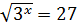
 2020-08-05
2020-08-05 268
268






