ОСНОВНЫЕ ТЕОРЕМЫ И ЗАДАЧИ ЕГЭ.
ЗАДАНИЕ1.
I. Нахождение процента от данного числа.
Найти р % числа А: Х= 
II. Нахождение числа по его проценту
Если р% какого-нибудь числа равно В, то это число равно: Х= В:  =
= 
III. Сколько процентов одна величина составляет от другой величины?
Число процентов, которое А составляет от В равно: 
 100%
100%
IV На сколько процентов одна величина отличается от другой.
Число А отличается от числа В на следующее значение процентов: 
 100%
100%
V Увеличение (уменьшение) числа на р%.
Если число А увеличить на р%, то получим число:А  (1+
(1+  )
)
Если число А уменьшить на р%, то получим число: А  (1-
(1-  )
)
ЗАДАНИЕ 2.
ЗАДАНИЕ 3.


 24
24
 5
5 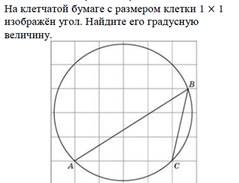 45
45
 4
4  30
30

 2.5
2.5
 2/З h
2/З h  1/3h
1/3h
 147
147  8
8
 6.4
6.4 
 2,5
2,5
 4/5
4/5  4
4

ЗАДАНИЕ 4.
0.25
 0.44
0.44
 0.375
0.375  0.33
0.33  0.06
0.06  0.4
0.4  0.003
0.003 
0.024
 0.19
0.19  0.08
0.08

0.35

0.33
 0.7
0.7

0.2425

0.17
 0.125
0.125 
0.0234

0.9604

0.32 
0.468 
0.75 
0.9271 
0.015

0.4


0.6

ЗАДАНИЕ5.

 -9
-9  3
3

 -3
-3  -1
-1
 4
4
 -6.5
-6.5  6
6
 8
8
 23
23
 -5
-5  -20
-20
 -0.25
-0.25
 0.7
0.7  7.5
7.5  5
5  0.5
0.5
 10
10
 32
32  -11
-11
 1
1
ЗАДАНИЕ6.









127

104

79

72

36

54
2.5 

17

12
0.6

26

100

4

7.2


3

6

56
 угол АВС=140,
угол АВС=140,
160

78

124

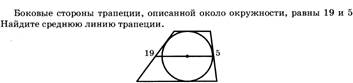
19

ЗАДАНИЕ 7.



Основные вопросы:
А: Изображен график функции:


Основные вопросы:
· Определите количество целых точек, в которых производная функцииотрицательна(положительна)?
· Найдите количество точек, в которых касательная к графику функции параллельна прямой. у=6?
· Найдите сумму точек экстремума?
· Найдите количество точек, в которых в которых производная функции равна 0?
· В скольких точках производная функции положительна(отрицательна)?
· Сколько точек лежит на промежутках возрастания (убывания) функции?
· В какой из точек значение производной наибольшее(наименьшее)
· На рисунке изображён график функции y = F (x) –одной из первообразных функции
· f (x),определённой на интервале (−2; 6). Найдите количество решений уравнения
f (x)= 0 на отрезке?
F (x) – рассматриваем как f (x), а f (x) - рассматриваем как f ¢(x)
В: Изображен график поизводной функции:

Основные вопросы:
· Найдите количество точек максимума(минимума) принадлежащих отрезку
[ а;в]?
· В какой точке отрезка [ а;в] функция принимает мах(мин) значение?
· Найдите количество точек экстремума?
· Найдите промежутки убывания(возрастания) и укажите:
· -длину наибольшего из них?
· -сумму целых точек в этом промежутке?
· Найдите координату точки экстремума(максимума, минимума) на отрезке?
· Найдите количество точек в которых производная функции равна нулю?
· Найдите количество точек в которых в которых касательная к графику функции:
· -параллельна прямой у=5 или совпадает?
· -параллельна прямой у= 2х-19 или совпадает с ней?
· -параллельна оси абсцисс или совпадает с ней
С. Текстовые задания на геометрический механический смысл производной:


 - это мгновенная скорость
- это мгновенная скорость
· Прямая y =2 x +37 является касательной к графику функции y = x 3+3 x 2−7 x +10. Найдите абсциссу точки касания.
· Материальная точка движется прямолинейно по закону
x (t) =1/2 t 3−3 t 2+2 t где x —расстояние от точки отсчета в метрах, t —время в секундах, измеренное с начала движения). Найдите ее скорость
· в момент времени t =6 с.
· Материальная точка движется прямолинейно по закону
· x (t) =1/3 t 3−3 t 2−5 t +3(где x —расстояние от точки отсчета в метрах, t —время в секундах, измеренное с начала движения). В какой момент времени ее скорость была равна 2 м/с
ЗАДАНИЕ 8.

4  8
8 
1500  5
5 
75  125
125 
4  9
9 
9  340
340 


12  3
3 
1.5  4
4 
0.25  6
6 
4.5  1.5
1.5 
3  3
3 
360  0.25
0.25 
ЗАДАНИЕ9.
Формулы сокращенного умножения:

Степени:



Свойства степени:

Арифметический корень:




Свойства арифметического корня:


Логарифмы и их свойства:






Основные тригонометрические формулы:




ЗАДАНИЕ10.

ЗАДАНИЕ 11.
ОСНОВНЫЕ ФОРМУЛЫ.
· Задачи на смеси:


· Задачи на проценты:


· Задачи на работу:



· Задачи на арифметическую прогрессию:



· Задачи на среднюю скорость:

· Задачи на движение протяженных тел:

Если тела двигаются навстречу друг другу то их скорости складываются.

 2020-08-05
2020-08-05 638
638







