Список формул сложения

Формулы сложения, доказательство, примеры.

Продолжением темы тригонометрические формулы служит данная статья про формулы сложения. Формулы сложения выражают синус, косинус, тангенс и котангенс суммы и разности двух углов поворота 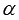и через тригонометрические функции этих углов. Сначала мы перечислим все формулы сложения, дальше приведем их доказательство, а в заключение покажем несколько примеров использования формул сложения.

Список формул сложения

Для начала перечислим все формулы сложения, и дадим их формулировки. Для удобства представим их в виде списка:

· Формула синуса суммы 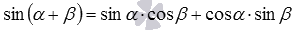- синус суммы двух углов равен сумме произведений синуса первого угла на косинус второго и косинуса первого угла на синус второго.

· Синус разности двух углов 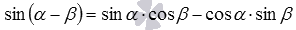- синус разности двух углов равен разности произведений синуса первого угла на косинус второго и косинуса первого угла на синус второго.

· Формула косинуса суммы 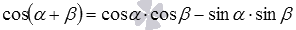- косинус суммы двух углов равен разности произведений косинусов этих углов и синусов этих углов.

· Косинус разности - косинус разности двух углов равен сумме произведений косинусов этих углов и синусов этих углов.

· Тангенс суммы .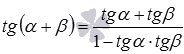

· Тангенс разности .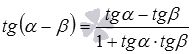

· Котангенс суммы .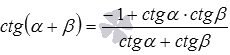

· Котангенс разности .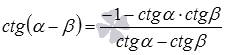

Отдавая дань краткости, формулы сложения обычно группируют две в одну, используя знаки плюс минус вида 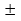и минус плюс . В таком виде они выглядят так:

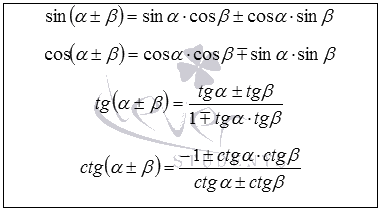
Каждая из записанных формул сложения соответствует двум формулам, перечисленным вначале этого пункта. Например, формула 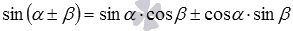отвечает двум формулам: синусу суммы (когда берется верхний знак из 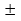) и синусу разности (когда берется нижний знак из ).

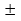Формулы сложения из таблицы называют соответственно формулами сложения для синуса, косинуса, тангенса и котангенса.

В заключение этого пункта отметим, что формулы сложения для синуса и косинуса справедливы для любых углов 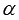и . А формулы сложения для тангенса и котангенса справедливы для всех 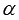и , для которых определены входящие в них тангенсы и котангенсы.

Доказательство

Начнем с доказательства формулы косинуса разности . Она нам поможет доказать другие формулы сложения.

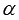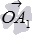Перед доказательством стоит озвучить один не очень очевидный факт, который мы используем. Он заключается в следующем. Возьмем единичную окружность. Пусть точки A₁ и A₂ получены в результате поворота начальной точки A(1, 0) вокруг точки O на углы и соответственно. Тогда угол между векторами и равен либо , либо 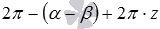, где z – любое целое число. Другими словами, угол между указанными векторами равен либо , либо 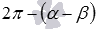, либо отличается от этих значений на целое число полных оборотов. Приведем графическую иллюстрацию для наглядности.

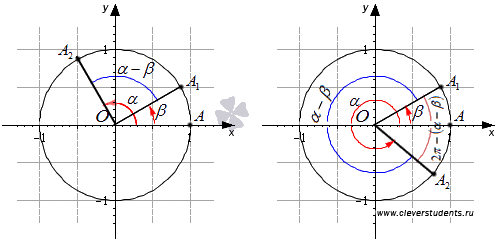
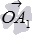Более того, формулы приведения позволяют нам записать следующие результаты и . Таким образом, косинус угла между векторами и равен косинусу угла , то есть, 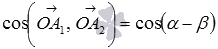. Теперь можно переходить непосредственно к доказательству формулы косинуса разности.

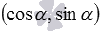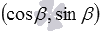В силу определений синуса и косинуса, точки A₁ и A₂ имеют координаты и соответственно. Тогда и 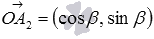(при необходимости смотрите координаты векторов через координаты точек их начала и конца). Длины этих векторов равны единице, так как они равны радиусу единичной окружности.

Теперь запишем скалярное произведение векторов 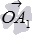и . С одной стороны имеем, а это же скалярное произведение в координатах имеет вид 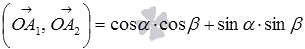. Отсюда получаем равенство . Этим доказана формула косинуса разности.

Переходим к доказательству следующей формулы сложения. Формулу косинуса суммы легко доказать, используя уже доказанную формулу и представление вида 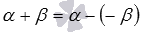. Имеем

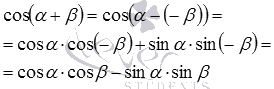
последний переход возможен в силу свойств синуса и косинуса противоположных углов.

Из формулы косинуса разности легко получить формулу синуса суммы, достаточно лишь обратиться к формуле приведения вида 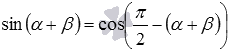. Так

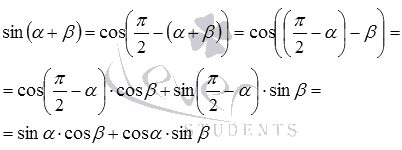
в последнем переходе мы использовали формулы приведения.

А вот доказательство формулы синуса разности:

в последнем переходе использовалось свойство синуса и косинуса противоположных углов.

Переходим к доказательству формул сложения для тангенса и котангенса. Для этого достаточно вспомнить, что тангенс – это отношение синуса к косинуса, а котангенс – отношение косинуса к синусу, а также применить доказанные выше формулы.

Так 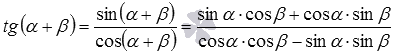. Теперь разделим числитель и знаменатель полученной дроби на 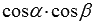, учитывая что 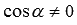и , имеем

после сокращения дробей получаем .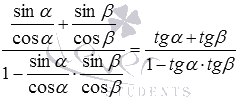
В итоге имеем .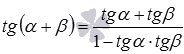

Теперь докажем формулу тангенса разности:

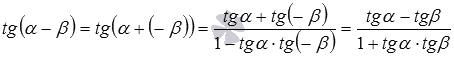
Формулы сложения для котангенса доказываются аналогично формулам сложения для тангенса:

и