Что и требовалось доказать

Алгебра

Контрольная работа.

Геометрия

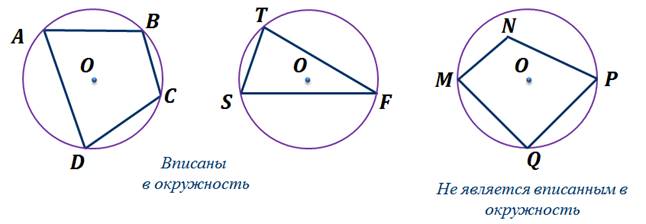
Определение. Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в эту окружность.

Докажем теорему об окружности, описанной около треугольника.

Теорема. Около любого треугольника можно описать окружность.

Доказательство.

.

.

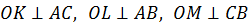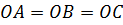Окружность проходит через все три вершины .

Окружность описана около .

Теорема доказана.

Замечания.

1. Около любого треугольника можно описать только одну окружность.

Доказательство.

Допустим, около треугольника можно описать две окружности.

Тогда центр каждой из них равноудален от его вершин и поэтому совпадает с точкой пересечения серединных перпендикуляров, проведенных к сторонам треугольника.

Радиус равен расстоянию от точки 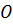до вершин треугольника.

Следовательно, эти окружности совпадают.

2. В отличие от треугольника около четырехугольника не всегда можно описать окружность.

Если же около четырехугольника можно описать окружность, то его углы обладают следующим замечательным свойством:

В любом вписанном четырехугольнике сумма противоположных углов равна .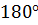

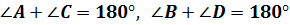
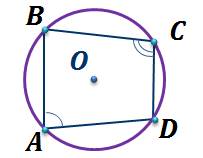
Доказательство.

Рассмотрим четырехугольник .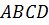

Докажем, что .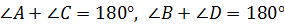

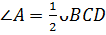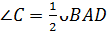и , то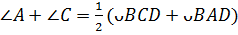

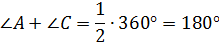
Значит, сумма противоположных углов вписанного четырехугольника равна .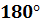

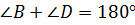
Что и требовалось доказать.

Аналогично доказывается, что
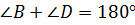. Это можно доказать и другим путем. Мы знаем, что сумма внутренних углов выпуклого четырехугольника равна 360º. Как мы уже доказали выше, сумма 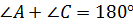. Значит, на сумму двух других углов (угла B и угла D) остается тоже 180º

Верно и обратное утверждение. Если сумма противоположных углов четырехугольника равна 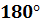, то около него можно описать окружность.

Доказательство

Рассмотрим четырехугольник .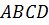

Пусть .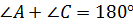

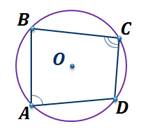
Докажем, что эта окружность проходит также через вершину .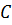

1) Вершина 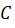может быть расположена внутри круга.

2) Вершина расположена вне круга.

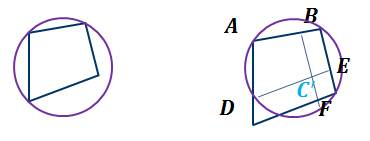
Тогда в четырехугольнике 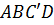будем иметь

.

.

.

.

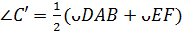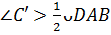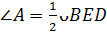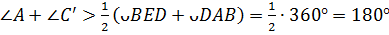Получили, что .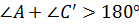

Следовательно, вершина 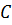лежит на окружности.

Что и требовалось доказать.

Как вы думаете, около прямоугольника можно описать окружность? Да! Ведь мы знаем, что у прямоугольника все углы равны девяноста градусам. А значит, сумма его противоположных углов составляет сто восемьдесят градусов. Следовательно, около прямоугольника можно описать окружность.

Задача. Найдите стороны остроугольного равнобедренного треугольника, если высота, проведенная к его основанию, равна 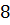см, а радиус окружности, в которую он вписан 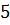см.

Решение.

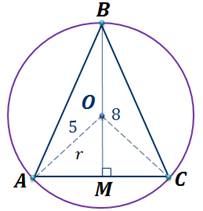
Пусть ABC – равнобедренный треугольник AB=BC, точка O – центр описанной около него окружности. BM высота треугольника ABC. Значит, она перпендикулярна стороне AC.

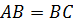
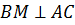
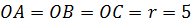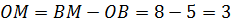(см)

(см)

Рассмотрим .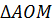

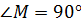
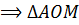– прямоугольный.

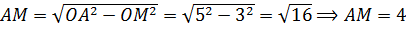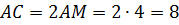(см).

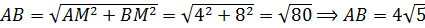(см).

(см).

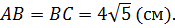
Ответ: 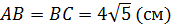, 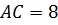(см).

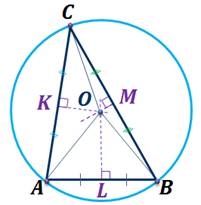
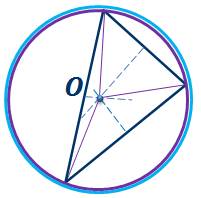
Давайте рассмотрим рисунок к задаче и укажем, где находится центр окружности описанной около треугольника. Проведем серединные перпендикуляры к сторонам треугольника.

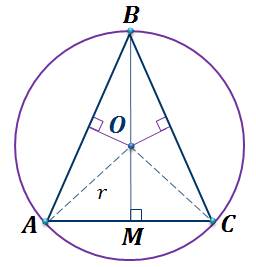
Напомним, что серединные перпендикуляры к сторонам треугольника, пересекаются в одной точке. Мы с вами уже говорили, что, так как треугольник ABC равнобедренный по условию, то высота BM является и его медианой, то есть она является и серединным перпендикуляром к стороне AC. Заметим, что точка пересечения серединных перпендикуляров совпала с центром окружности описанной около треугольника.

Следовательно, верно утверждение: перпендикуляры, восстановленные к серединам сторон треугольника (серединные перпендикуляры) пересекаются в одной точке, которая является центром описанной окружности.

Повторим главное:

На этом уроке мы узнали, что если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в эту окружность. Доказали, что около любого треугольника можно описать окружность. А вот, что около четырехугольника не всегда можно описать окружность. И также узнали, что в любом вписанном четырехугольнике сумма противоположных углов равна 180º.

Переписать!!!