Самостоятельная работа

Тема: Геометрические преобразования пространства.

Задание: изучить теоретические основы темы по конспекту или учебнику (Геометрия. Учебник для 10-11 классов - Атанасян Л.С., глава V, §3, п. 56-58), решить задачи самостоятельной работы и ответить письменно на контрольные вопросы.

Теоретический минимум и задачи

Геометрические преобразования имеют большое значение в геометрии. С помощью геометрических преобразований определяются такие важные геометрические понятия, как равенство и подобие фигур. Благодаря геометрическим преобразованиям, многие разрозненные факты геометрии укладываются в стройную теорию.

Для начала обратимся к некоторым основным понятиям, которые будут необходимы нам для работы с преобразованиями. Остановимся на двух терминах: расстояние и преобразование.

Определение. Расстоянием между двумя точками будем называть длину отрезка с концами в этих точках.

Определение. Преобразованием пространства называется взаимно-однозначное отображение пространства на себя.

Два преобразования называются равными, если образы любой точки при этих преобразованиях совпадают.

Точка А называется неподвижной точкой при некотором преобразовании f, если при этом преобразовании она отображается на себя.

Фигура F называется неподвижной фигурой при некотором преобразовании f, если при этом преобразовании она отображается на себя.

Преобразование пространства, которое каждую точку отображает на себя, называется тождественным преобразованием. Оно обычно обозначается Е. При тождественном преобразовании все точки и все фигуры пространства являются неподвижными.

Для любых двух преобразований можно рассмотреть третье, которое получается последовательным применением этих преобразований. Например, если преобразование f отображает точку М на точку М', а преобразование g отображает точку М' на точку M'', то преобразование f°g отображает точку М на точку M'': f°g(М)=g(f(M))=M''.

f°g - композиция преобразований f и g.

Под движением пространства понимается отображение пространства на себя, при котором любые две точки A и B переходят (отображаются) в некие точки A1 и B1 так, что |AB|=|A1B1|.

Движение пространства — это отображение пространства на себя, сохраняющее расстояния между точками. Так же, как и для движения на плоскости, можно доказать, что при движении в пространстве

- прямые переходят в прямые,

- полупрямые — в полупрямые,

- отрезки — в отрезки,

- сохраняются углы между прямыми.

Новое свойство движения в пространстве: движение переводит плоскости в плоскости.

В пространстве, так же как и на плоскости, две фигуры называются равными, если они совмещаются движением.

Можно доказать, что композиция двух движений пространства есть движение.

Ранее мы рассмотрели симметрии в пространстве: центральную, осевую, зеркальную. Такие преобразования являются движением. Теперь перейдём к рассмотрению других видов геометрических преобразований.

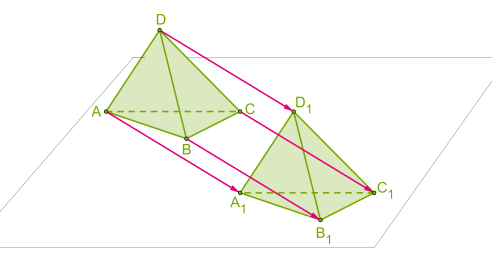
Параллельный перенос (точки переносятся на данный вектор):

Определение

Пусть дан вектор 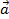. Преобразование пространства, при котором каждая точка пространства M, отображается на такую точку M', что выполняется равенство 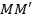, называется параллельным переносом на вектор .

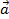Перенос на нулевой вектор 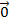является тождественным преобразованием.

Параллельный перенос отображает прямую на параллельную ей прямую либо на себя; плоскость на параллельную ей плоскость либо на себя.

Неподвижных точек параллельный перенос на ненулевой вектор не имеет.

Неподвижными прямыми при параллельном переносе на вектор 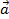являются прямые, параллельные этому вектору.

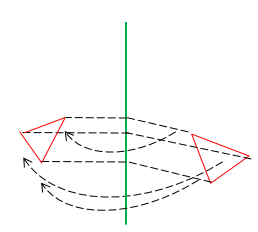Неподвижными плоскостями при параллельном переносе на вектор 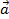являются плоскости, параллельные этому вектору.

Поворот на данный угол вокруг данной оси:

Определение:

Поворотом пространства на угол φ вокруг прямой n называется такое преобразование пространства, при котором любая точка прямой остается неподвижной и в любой плоскости, перпендикулярной прямой n, осуществляется поворот этой плоскости на угол φ вокруг точки ее пересечения с прямой n.

 

Неподвижными точками являются любая точка оси вращения.

Неподвижной прямой является ось поворота.

Неподвижной плоскостью является любая плоскость, перпендикулярная оси поворота.

Поворот вокруг оси на угол 180⁰ является осевой симметрией.

Рассмотрим примеры решения задач.

Задача № 478

а) При центральной симметрии относительно точки О (0;0;0):  х₂ = -х₁; у₂ = -у₁; z₂ = -z₁.

А(0;1;2) —> А₁(0;-1;-2),

В(3;-1;4) —> В₁(-3;1;-4),

С(1;0;-2) —> С₁(-1;0;2)

б) При осевой симметрии относительно оси Ох: х₂ = х₁; у₂ = -у₁; z₂ = -z₁.

А(0;1;2) —> А₁(0;-1;-2),

В(3;-1;4) —> В₁(3;1;-4),

С(1;0;-2) —> С₁(1;0;2)

в) При зеркальной симметрии относительно Ozy х₂ = -х₁; у₂ = у₁; z₂ = z₁.

А(0;1;2) —> А₁(0;1;2),

В(3;-1;4) —> В₁(-3;-1;4),

С(1;0;-2) —> С₁(-1;0;-2)

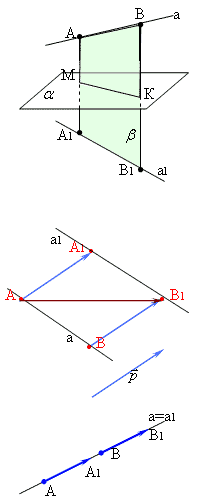
Задача № 482

Дано: Sa (а) = а ₁

Доказать: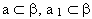

Решение:

 

 

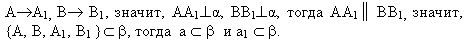
Самостоятельная работа

Задача № 1 

Найти координаты точек, в которые переходят точки A(3;-1;2); B(2;0;3) при: симметрии относительно точки О (0;0;0); осевой симметрии относительно оси Оy и Оz.; зеркальной симметрии относительно Охy.

Задача №479

Контрольные вопросы.

1. Перечислите виды симметрий в пространстве.
2. Почему симметрии являются движением в пространстве?
3. Какие ещё виды преобразований пространства вы знаете?