Соответствие между множествами

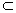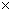Соответствием между множествами X и Y называется всякое подмножество декартова произведения этих множеств. Соответствия принято обозначать буквами P, S, T, R и др. Если xSy – соответствие между элементами множеств X и Y, то, соглаcно определению, S X Y.

Поскольку соответствие – это подмножество, то его можно задать как любое множество, т.е. либо перечислив все пары элементов, находящихся в данном соответствии, либо указав характеристическое свойство элементов этого подмножества. Например, соответствие между множествами X={1, 2, 4, 6} и Y={3, 5} можно задать:

1) при помощи предложения двумя переменными: a<b при условии,

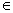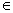что a X, b Y;

    2) перечислив пары чисел, принадлежащих подмножеству декартова произведения X 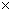Y: {(1, 3),(1, 5), (2, 3), (2, 5), (4, 5)}.

Графом в математике называется конечная совокупность точек, называемых вершинами графа; некоторые из них соединены друг с другом линиями, которые называются ребрами графа.

График соответствия представляет собой изображение множества X 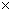Y в виде точек на координатной плоскости. Представление соответствия в виде графа и графика позволяет изображать его в тех ситуациях, когда в заданном соответствии находится бесконечное множество пар чисел.

Пусть на множествах X=R, Y={4, 6} задано соответствие «больше». Так как в заданном соответствии находится бесконечное множество пар, то такое соответствие можно представить лишь наглядно.

Множество Х называют областью отправления соответствия R, множество Y – областью прибытия.

Совокупность А всех элементов из Х, имеющих непустые образы, называют множеством определения соответствия R. Множество В всех элементов из Y, имеющих непустой полный прообраз, называют множеством значений соответствия R.

Если график соответствия R между множествами Х и Y совпадает со всем декартовым произведением X 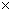Y, то соответствие называют полным. Если же график пуст, то R называют пустым соответствием.

Над соответствиями можно выполнять различные операции.

Если между множествами Х и Y заданы соответствия xPy и xQy, то их пересечением R=P 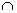Q называют соответствие xRy, график которого является пересечением графиков данных соответствий.

Объединением S=P 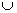Q данных соответствий называют соответствие xSy, график которого является объединением графиков соответствий xPy и xQy.

Если графики соответствий xPy и xQy – дополнительные множества в X 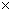Y (т.е. не пересекаются, а в объединении дают X 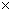Y), то такие соответствия называют противоположными. Например, соответствие «число х больше числа y» и соответствие «число х не превосходит числа y».

Соответствия P и Q называют несовместимыми, если не существует ни одной пары (х;y), для которой одновременно выполнялись бы условия xPy и xQy. Например, для прямых x 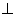y и x||y соответствия несовместимы.

Например,рассмотрим S – соответствие «больше на 2» между множествами S={4, 5, 8, 10} и Y={2, 3, 6}. Тогда соответствие

S={(4; 2), (5; 3), (8; 6)}, а S 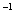={(2; 4), (3; 5), (6; 8)}. Такое соответствие называется обратным данному.

 

Пусть S – соответствие между множествами Х и Y. Соответствие S 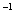между множествами Y и Х называется обратным данному, если yS 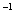x тогда и только тогда, когда xSy. Соответствия S и S 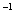называют взаимно обратными.

В математике изучают различные виды соответствий. Это не случайно, поскольку взаимосвязи, существующие в окружающем нас мире, многообразны. Особую значимость имеют взаимно однозначные соответствия.

Рассмотрим примеры таких соответствий.

Пусть Х – множество кружков, Y – множество квадратов. Соответствие между ними задано при помощи стрелок.

Это соответствие взаимноодназначное, так как каждому кружку сопоставляется единственный квадрат и каждому квадрату сопоставляется единственный кружок.

Рассмотрим другой пример. Пусть А – множество всех четных натуральных чисел, В – множество всех нечетных натуральных чисел. Каждому четному числу поставим в соответствие число, на единицу меньше:

Получим взаимно однозначное соответствие между бесконечными множествами А и В.

Таким образом, взаимно однозначным соответствием между множествами Х и Y называется такое соответствие, при котором каждому элементу множества Х сопоставляется единственный элемент множества Y и каждый элемент множества Y соответствует только одному элементу множества Х.

Установим соответствие между элементами множеств А и В с помощью графа, если А={a, b, c, d}, B={1, 2, 3, 4}.
Множества Х и Y называются равномощными, если между ними можно установить взаимно однозначное соответствие.

Пусть Х – множество точек отрезка АВ, а Y – множество точек отрезка СD, причем длины отрезков различны. Так как между данными множествами можно установить взаимно однозначное соответствие (рис. 27), то множества точек отрезка АВ и СD равномощны.

Равномощными могут быть как конечные, так и бесконечные множества. Например, множество четных чисел и множество нечетных чисел. Если бесконечное множество равномощно множеству натуральных чисел N, то его называют счетным. Но среди бесконечных множеств можно найти и такие, которые не будут эквивалентны между собой. Например, множество натуральных чисел и множество всех точек координатной прямой.
Отношение равномощности обладает рядом свойств:

– Рефлексивность (каждое множество равномощно самому себе: Х~Х).

– Симметричность, т.е. X~Y и Y~X.

– Транзитивность, т.е. если множество Х равномощно множеству Y, множество Y равномощно множеству Z, то множество Х равномощно множеству Z: X~Y и Y~Z 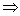X~Z.