Параметры счётчиков числа импульсов

Основные параметры ИМС счётчиков можно разделить на две группы: статические и динамические. К статическим параметрам относятся: модуль счёта К, ёмкость счётчика Е, разрядность счётчика n, выходное напряжение высокого U¹_вых и низкого U⁰_вых уровней, входное напряжение высокого U¹_вх и низкого U_вх уровней, входной ток низкого I_вх и высокого I_вх уровней, ток потребления I_n, выходные токи I⁰_вых и I¹_вых ток в состоянии "выключено" I_oz. К динамическим параметрам относятся:

   ¤ время задержки распространения сигналов при включении _.;

  ¤ время задержки распространения сигналов при выключении _.;

При этом указанные задержки сигналов _., при включении и _.

при выключении измеряют для случая их распространения в следующих направлениях:

• от тактовых входов CU и CD к выходам прямого и обратного переноса 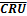  и ;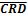

• от тактовых входов CU     и      CD к выходам данных Q_n,Q_n-1,...,Q₁,Q_o;

• от входа выбора направления счёта D/ 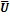   к выходу переноса MAX/MIN;

• от входа выбора направления счёта D/ 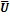 к выходу наращивания счёта ;

• от входа тактирования CLK к выходам данных Q_n,...,Q₁,Q_o;

• от входа разрешения параллельной загрузки 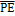 к выходам данных Qn,...,Q₁Q₀;

• от входов данных D_n,...,D₁,D₀ квыходам данных Q_n,...,Q₁,Q_o;

• от входа тактирования CLK к выходу наращивании счёта ;

• от тактового входа CLK к выходу переноса MAX/МIN;

• от входа разрешения счёта 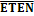   к выходу наращивания счёта ;

• от входа установки в состояние логический "0" R к выходам данных Q_n,...Q₁,Q₀;

• от входа разрешения переноса ECR к выходу переноса CR
¤ максимальная частота счёта F_max.

10

Максимальная частота F_max следования счётных импульсов определяется из соотношения:

                         F_max=1/(t_n +t_зд.max)          (10.2)

где t_n - длительность счётных импульсов;

t_зд.max - максимальная из числа перечислимых выше задержка рас-пространения сигналов для данной ИМС

Для оценки быстродействия счётчиков используют следующие динамические параметры: усреднённое время задержки распространения сигналов Т_зд от его входов к выходам и максимальную частоту счёта F_max. При этом

                                                                                                           

 

 (10.3)

  

                                                        

где  - время задержки распространения сигнала при включении

и выключении в процессе реализации j-ой и i-ой операций переключения из числа названных выше.

Поясним смысл некоторых параметров из числа перечислимых выше. Это относится прежде всего к тем параметрам, смысл которых либо не являются очевидным, либо содержит определённую многозначность. К примеру, наряду с понятием модуль счёта К применяют такие понятия, как максимальный модуль счета К_м, модуль каскадного счетчика К_к, модуль программируемого счётчика К_пр и др.

• Модуль счёта (коэффициент пересчёта или период счётчика) К - это число, равное количеству входных счетных (тактовых) импульсов, по­сле поступления которых при неизменном направлении счета (±) счетчик возвращается в исходное состояние.

• Максимальный модуль счёта К_м - это число, равное максимально возможному числу состояний счетчика. Максимальный модуль К_м и число разрядов n двоичного счетчика связаны соотношением:

К_м =2ⁿ                                   (10.4)

Модуль каждой декады двоично-десятичного счётчика равен К_д =10.

11

• Модуль каскадного счётчика К_к - это число, равное произведению модулей счётчиков К₁,K₂,...,К_к, входящих в каскадное соединение.

 

                            (10.5)

где К_j - модуль счёта j - го счётчика.

• Модуль программируемого счётчика К_пр - это модуль многорежимного счётчика, у которого режим работы и модуль задаются с помощью кода управления {A_n,...,A₁,A₀} в соответствии с соотношением (10.1)

• Ёмкость счётчика Е равна максимальному числу, которое может быть в нём представлено. В двоичных счётчиках ёмкость Е определяется из соотношения

Е= 2ⁿ-1                                    (10.6)

• Разрядность счётчика n определяется числом его триггеров. Для
двоичньгх счётчиков

n=log₂K_м                               (10.7)

Промышленность выпускает большое количество ИМС четырёхразрядных двоичных счётчиков ТТЛ, КМОП и ЭСЛ технологий. Эти счётчики имеют: n =4 разрядов, К_м =2⁴=16, Е = 2⁴-1 = 15. В таблице 10.1. приведены некоторые типы 4-разрядных счётчиков различных ТТЛ и КМОП серий интегральных микросхем. Параметры КМОП ИМС счётчиков, представленных в таблице 10.1, соответствуют их режимам работы при напряжении источника питания, равном +5В. При этом на входах и выходах КМОП ИМС напряжение высокого и низкого уровней имеют следующие значения величин:

 

Аналогичные параметры для ТТЛШ счётчиков соответственно равны:

Таблица 10.1

 

13

В таблице 10.1 в графе "Наименование счётчика" приведены регла­ментируемые ГОСТ - ами условные обозначения (маркировка) счетчиков.

Система условных обозначений ИМС счётчиков включает следую­щие элементы: одна, две или три первые буквы указывают на область при­менения, характеристику материала и тип корпуса; три или четыре сле­дующие цифры определяют конструктивно-технологический признак и номер серии ИМС; последующие две буквы обозначают функциональное назначение ИМС; заключительные от одной до трёх цифр - порядковый номер разработки в данной серии среди ИМС одного вида. Например, в обозначении счетчика типа КР1533ИЕ7 имеем:

 

 

В таблице 10.2 приведены параметры двоично-десятичных счетчи­ков популярных ТТЛШ и КМОП серии интегральных микросхем, а в таб­лице 10.3 - параметры ЭСЛ, ТТЛШ и КМОП счетчиков, имеющих особен­ности в организации функционирования, контролепригодности, разрядно­сти, режимах работы и др.

14

 

 

15

10.4. Граф переходов счетчика

Граф переходов счетчика - это диаграмма смены его состояний при работе в различных режимах. Граф переходов представляется в наглядной форме. На рис.10.2,...,рис.10.5 приведены графы переходов основных раз­новидностей четырехразрядных счетчиков: двоичного суммирующего счетчика (рис. 10.2), двоично-десятичного счетчика (рис. 10.3), двоичного реверсивного счетчика (рис. 10.4) и двоично-десятичного реверсивного счетчика (рис. 10.5).

Вершины (узлы) графа изображаются различными геометрическими фигурами (окружностями, точками, прямоугольниками и др.), которые по­мечают надписями с целью их идентификации. На рис.10.2,...,10.5 вер­шины графов выполнены в виде прямоугольников, а надписи в прямо­угольниках соответствуют состояниям счетчика, обозначенным десятич­ными числами от 0 до 15. Фактически состояния двоичных и двоично-де­сятичных счетчиков отображается в виде двоичных кодов на выходах счетчика, поэтому зачастую надписи в узлах графов выполняют непосред­ственно в двоичных кодах. В таблице 10.4 дано взаимное соответствие указанных отображений состояний счетчиков.

Таблица 10.4.

 

Представление состояний счетчика
На рис.10.2,...,10.5	На выходах счетчика	На рис.10.2,...,10.5	На выходах счетчика
0	0000	8	1000
1	0001	9	1001
2	0010	10	1010
3	0011	11	1011
4	0100	12	1100
5	0101	13	1101
6	0110	14	1110
7	0111	15	1111

Пары различных вершин графа переходов соединяют ориентирован­ными дугами (ребрами). Ребра графа изображаются линиями, соединяю­щими соответствующие вершины. Графы переходов счетчиков рис. 10.2,... 10.5 являются ориентированными графами (орграфами), так

16

 

 

                                                                Рис.10.3

17

Рис. 10.4.

 

 

Рис.10.5

18

как каждому их ребру приписывают направление. Стрелки на ребрах графа указывают направление перехода от данного состояния к следующему со­стоянию счетчика. К примеру, если в рассматриваемый момент времени, реверсивный двоичный счетчик находится в состоянии 9 (рис. 10.4), то при поступлении счетного импульса он переходит в состояние 10 при его рабо­те в режиме суммирования, либо в состояние 8 при реализации режима вычитания. Условия, при которых осуществляется данный переход, оформ­ляют в виде надписей на ребрах графа, либо отображаются с помощью графических различий ребер графа. В частности, на рис.10.4 и рис. 10.5 сплошными линиями изображены ребра графа, соответствующие режиму счета на увеличение (режим суммирования), а пунктирными линиями - режиму счета на уменьшение (режим вычитания).

Таблица 10.5

Количество	Состояния
счетных	счетчика
сигналов
0	0000
1	0001
2	ООП
3	0010
4	ОНО
5	0111
6	0101
7	0100
8	1100
9	1101
10	1111
11	1110
12	1010
13	1011
14	1001
15	1000

В том случае, когда счетчик работает не в режиме естественно­го двоичного счета, а реализует счет в кодах с искусственным по­рядком весов в соответствующих разрядах, то коды его состояний будут отличаться от представлен­ных в таблице 10.4. В качестве примера в таблице 10.5 дано коди­рование состояний четырехраз­рядного счетчика с искусственным порядком счета в коде Грея.

Состояния счетчиков из таб­лиц 10.4 и 10.5 повторяются с пе­риодом 2ⁿ, поэтому для сокраще­ния графов переходов и таблиц состояний в них показывают со­стояния только для одного перио­да.

19