Теоретические сведения

ИССЛЕДОВАНИЕ ОБНАРУЖИТЕЛЕЙ СИГНАЛА

 

Лабораторная работа № 2

по дисциплинам

«Перспективные методы обработки сигналов РТС»

«Моделирование и оптимизация систем связи»

 

Цель работы: Изучение методов и алгоритмов обнаружения сигнала на шумовом поле с известными и неизвестными характеристиками.

 

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

1.1. Формулировка задачи обнаружения

В лабораторной работе рассматривается случай обнаружения локального сигнала, занимающего один элемент (пиксел) или группу смежных элементов на изображении. Обычно появление сигнала связано с увеличением интенсивности (яркости) в этих элементах изображения по отношению к случайной яркости фона. Для сигнала, занимающего один элемент, его обнаружение на шумовом фоне может осуществляться путем сравнения каждого значения поля с порогом. Если сигнал занимает группу элементов, то формирование решающей статистики осуществляется в процессе группирования соответствующих элементов изображения.

При известных характеристиках сигнала и шумового поля порог является постоянным и может быть рассчитан заранее исходя из выбранного критерия обнаружения. В данной работе применяется критерий Неймана-Пирсона, который обеспечивает наибольшую вероятность правильного обнаружения при фиксированной вероятности ложной тревоги.

Задача обнаружения формулируется как задача проверки гипотезы 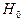: сигнала нет, против гипотезы (альтернативы) 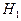: сигнал есть.

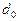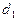Наблюдения зависят от вида излучения, формы полезного сигнала, типа помехи и вида ее взаимодействия с сигналом, а также от структуры предварительной обработки. Решения  и , принимаемые в пользу  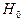и 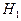, зависят как от самих событий (появление сигналов в отдельных элементех), так и от наблюдений и способа обработки, т. е. от вида радиотехнической системы и алгоритма обнаружения.

Пусть 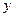 – случайная величина, представляющая наблюдение в данном элементе изображения, либо наблюдение, полученное в результате группирования сигнальных выборок из нескольких элементов изображения. Тогда при гипотезе  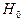случайная величина  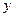имеет плотность вероятности 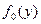, а при альтернативе  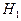– плотность вероятности 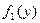. Оптимальный алгоритм обнаружения основан на формировании отношения правдоподобия (решающей статистики)  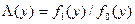и сравнении его с порогом 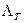, т. е. при  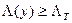принимается решение  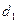в пользу гипотезы 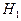, а при  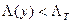– решение  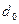в пользу гипотезы 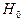. Если  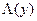есть монотонная функция 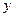, то оптимальный алгоритм имеет эквивалентный вид 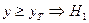. В других случаях последний алгоритм уже не будет оптимальным.

Значение порога 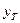 существенно зависит от вида и параметров распределения фона и распределения сигнала в анализируемых элементах изображения. При полном статистическом описании моделей сигнала и фона это значение может быть рассчитано заранее. Это значение зависит от выбранного критерия оптимальности. Для критерия Неймана-Пирсона порог  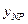рассчитывается исходя из заданной вероятности ложной тревоги.

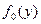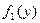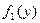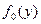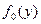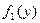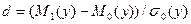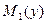Качество обнаружения зависит от степени различия плотностей  и . Это различие обычно растет с увеличением интенсивности полезного сигнала и проявляется, в частности, в сдвиге  по отношению к . Степень различия плотностей  и  влияет на степень обнаружимости полезного сигнала и ее можно характеризовать параметром обнаружения , где  и 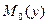 обозначают математические ожидания случайной величины (СВ)  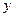при гипотезах  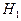и 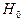,  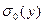– среднеквадратическое отклонение (СКО) СВ  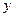при гипотезе 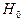. Параметр  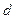называется дефлекцией и обычно имеет физический смысл отношения сигнал/шум по напряжению на входе порогового устройства.

Другим параметром обнаружения, характеризующим степень обнаружимости, является величина 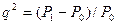, где 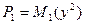,  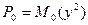- вторые моменты распределени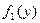й  и 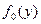, т. е. мощности случайной величины  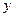при соответствующих гипотезах. Величина  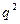имеет смысл отношения сигнал/шум по мощности на входе порогового устройства.

Качество алгоритма обнаружения при заданном различии плотносте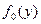й  и 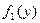 (т. е. при заданном отношении сигнал/шум в какой-либо форме) полностью характеризуется двумя условными вероятностями: вероятностью ложной тревоги  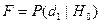и вероятностью правильного обнаружения 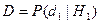. Вместо вероятности правильного обнаружения можно использовать вероятность пропуска .

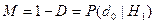Зависимость 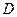 от 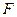 при фиксированном параметре обнаружения (или фиксированном отношении сигнал/шум) есть рабочая характеристика приемника (РХП). Зависимость  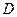от параметра обнаружения при фиксированной вероятности ложной тревоги представляет характеристику обнаружения алгоритма или кривую обнаружения. Семейства этих кривых связаны с семействами РХП, но при использовании критерия Неймана-Пирсона удобнее пользоваться характеристиками обнаружения.

Для байесовских критериев идеального наблюдателя и максимального правдоподобия качество обнаружения описывается вероятностями полной ошибки 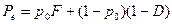 и суммарной ошибки  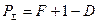соответственно. Здесь  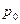есть априорная вероятность отсутствия сигнала. Для описания качества алгоритмов используются зависимост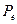и  или 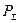 от параметра обнаружения.

 

1.2 Обнаружители с постоянным порогом в случае модельных распределений фона

 

При полностью известной плотности 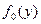 вычисление порога  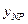по критерию Неймана-Пирсона сводится к решению уравнения 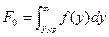, где 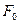 – заданное значение вероятности ложной тревоги. Фактически требуется определить процентную точку выбранного распределения. Для большинства модельных распределений решение получается в аналитическом виде.

 

1.3 Расчет постоянного порога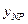

B случае равномерного распределения 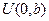 пороговое значение равно .

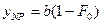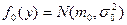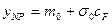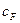Для гауссовского распределения  порог равен , где  есть 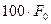 – процентная точка стандартного нормального распределения 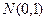. Значение  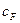выбирается по таблицам интеграла вероятности исходя из заданного значения 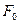. Связь значени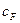й  и 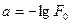 дается таблицей 1:

Таблица 1

 

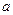
	2	3	4	5	6
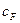
	2,323	3,09	3,72	4,27	4,76

 

Шум с экспоненциальным распределением образуется на выходе квадратичного детектора огибающей при воздействии на его вход гауссовского шума с нулевым математическим ожиданием. Шум с релеевским распределением получается на выходе линейного детектора огибающей.

В случае шума с экспоненциальным распределением 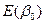 решение получается в виде 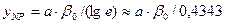. Для релеевского распределения  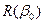порог равен .

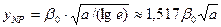Вообще для шума с распределением из семейства Вейбулла 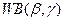 значение .

 

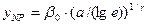В случае шума с логарифмическим нормальным распределением 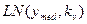 порог равен .

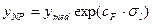Для шума с гамма-распределением 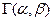 порог выражается через процентную точку  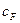стандартного гамма-распределения 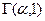. Последняя связана с неполной гамма-функцией 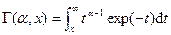, а именно 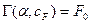. Порог по критерию Неймана-Пирсона будет равен .

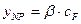При больших аргументах 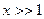 имеется асимптотическое разложение .

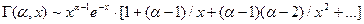Для целых 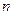 справедливо выражение 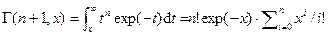. Известно, что гамма-распределение есть непрерывный аналог распределения хи-квадрат, причем число степеней свободы  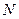последнего распределения связано с параметром формы гамма-распределения 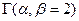, а именно 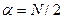. Процентные точки распределения  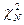с 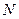 степенями свободы приведены в таблице 2.

Процентные точки гамма-распределения 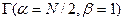 будут вдвое меньшими. Для определения процентной точки при другом параметре масштаба  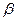следует взять значение из таблицы, разделить на два и умножить на .

 

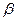Таблица 2

 

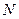
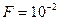
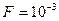
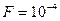
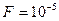
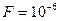
1	6,635	10,828	15,137	19,511	23,928
2	9,21	13,816	18,421	23,026	27,631
5	15,086	20,515	25,745	30,856	35,888
10	23,209	29,588	35,564	41,296	46,863
20	37,566	45,315	52,386	59,045	65,421
30	50,892	59,703	67,633	75,023	82,044
50	76,154	86,661	95,969	104,542	112,608
100	135,807	149,449	161,319	172,099	182,127

 

В случае шума с 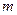 - распределением Накагами  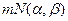также можно пользоваться указанной таблицей для 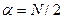. Распределение Накагами может быть получено из гамма-распределения путем функционального преобразования, которое сводится к извлечению квадратного корня. Для определения процентной точки, т. е. порога 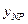, берется значение из таблицы для заданных  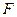и 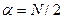, делится пополам, извлекается квадратный корень, и результат умножается на параметр масштаба распределения Накагами.

 

Для шума с 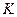 - распределением  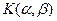порог можно вычислить приближенно. Вероятность превышения порога равна 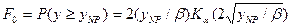, где 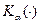 – модифицированная функция Бесселя второго рода. При больших аргументах  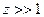она вычисляется приближенно по формуле 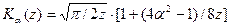. Порог  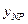определяется из полученного приближенного уравнения.