Линейные средства измерений с сосредоточенными параметрами

Наиболее часто для получения общего решения линейных дифференциальных уравнений с постоянными коэффициентами, которыми описываются стационарные СИ с сосредоточенными параметрами, на практике используются классический метод и преобразования Лапласа или Карсона — Хевисайда. Рассмотрим сущность и особенности использования этих методов для анализа математической модели СИ и определение основных динамических характеристик.

Как было показано в гл. 4, линейное аналоговое СИ может быть описано системой или одним линейным уравнением (2.99), (2.100) в операторной форме:

(5.1)

или

(5.2)

где N (р) — операторный многочлен; 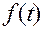— неинформативный параметр входного сигнала, возмущающее воздействие и т. д.

Согласно классическому методу, полное решение неоднородного уравнения (5.1) или (5.2)

(5.3)

где — общее решение однородного уравнения ;

— частное решение уравнения (5.2).

Общее решение однородного уравнения (5.2):

(5.4)

где — корни однородного характеристического уравнения ; — кратности корней; — произвольные постоянные.

Если отсутствуют нулевые и кратные корни, то (5.4) приобретает более простой вид:

(5.5)

где r — число вещественных корней однородного характеристического уравнения; l — число пар комплексно сопряженных корней характеристического уравнения.

Частное решение определяется правой частью уравнения (5.2) и соответствует некоторому установившемуся (статическому) режиму, который будет существовать после затухания свободной составляющей . Например, при решение может складываться из отдельных слагаемых, определяемых правой частью. Для уравнения (5.2) будет два слагаемых, получаемых из уравнений

В этом заключается принцип суперпозиции.

Для определения произвольных постоянных и используются начальные условия при t = 0: Начальные условия находят из физических соображений или по уравнению (5.2). При этом для определения произвольных постоянных необходимо использовать полное решение (5.3). Например, для случая вещественных корней

(5.6)

Дифференцируя (5.6) п — 1 раз по времени и приравнивая (5.6) и получаемые выражения или в соответствии с начальными условиями получим п алгебраических уравнений для отыскания произвольных постоянных.

При определении переходной или импульсной характеристики на вход СИ подаются тестовые сигналы — единичные ступенчатый сигнал или идеальный импульс. Следовательно, для их определения реальный входной сигнал в уравнении (5.1) необходимо заменить на или

Решение уравнений классическим методом — довольно трудоемкий процесс, особенно отыскание произвольных постоянных интегрирования. Поэтому часто для решения используются преобразования Лапласа.

Метод решения дифференциальных уравнений с использованием преобразований Лапласа состоит в замене дифференциальных уравнений алгебраическими, результат решения которых затем преобразуется в искомые временные функции.

Преобразование Лапласа, или изображение F (р) временной функции f (t), определяется как

(5.7)

или для выходного сигнала

Поскольку 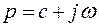— комплексная величина, то результат решения в изображениях получается в области комплексного переменного.

Для отыскания временной функции или оригинала у (t) по найденному решению У (р) используется обратное преобразование Лапласа

(5.8)

Выражения (5.7) и (5.8) справедливы для случая нулевых начальных условий, то есть

у (t) = 0 при t = 0.

Широкое распространение преобразований Лапласа для решения дифференциальных уравнений объясняется, во-первых, возможностью решения алгебраических, а не дифференциальных уравнений; во-вторых, «автоматическим» учетом начальных условий в самих преобразованиях и, наконец, тем, что трудоемкая операция отыскания интегралов (5.7) и (5.8) сведена к использованию нескольких теорем и таблиц преобразования элементарных функций.

Изображения и оригиналы некоторых функций, а также основные теоремы преобразовании Лапласа, используемые для решения дифференциальных уравнений, приведены в табл. 5.1.

Найдем решение линейного дифференциального уравнения (5.1) с нулевыми начальными условиями.

Согласно теореме дифференцирования и свойству линейности (табл. 5.1), уравнение (5.1) в изображениях будет

(5.9)

Значение изображения выходной величины У (р) в комплексной области может быть определено как

(5.10)

или через передаточную функцию

(5.11)

Для отыскания оригинала необходимо воспользоваться обратными преобразованиями Лапласа (5.8) или таблицей преобразований, предварительно разложив, при необходимости, правую часть (5.10) на дроби.

Если рассматриваются ненулевые начальные условия, то есть , то их необходимо учесть в преобразованиях Лапласа. Изображение первой производной в этом случае можно получить на основании (5.7):