Лекция 1
§ 1. Основные топологические определения
Определение 1: Множество (мн-во) – это совокупность объектов любой ( ) природы, объединенных по каким-то признакам.
) природы, объединенных по каким-то признакам.
Обозначения: A,B,C,…,X,Y,… - множества; a,b,c,…,x,y,… - элементы.
Топология– раздел математики, изучающий свойства (св-ва) геометрических фигур при некоторых их преобразованиях, при условии, что фигура может растягиваться, изгибаться, сжиматься, но не может разрываться или «склеиваться».
Определение 2: δ-окрестностью точки М0 ϵ ℝ называется (def) мн-во точек пространства ℝn, расстояние которых до точки М0 больше δ:
Uδ (M0) = {M ϵ ℝn: ρ(M, M0) < δ},
где ρ(M, M0) – расстояние между точками (…) M и M0.
Примеры:
При n =1 Uδ (M0) = Uδ (x0) {x ϵ ℝ: | x- x0 |< δ},
xo- 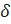 xo xo-
xo xo- 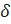
При n =2 Uδ (M0) = Uδ (x0, yo) {(x,y) ϵ ℝ2: 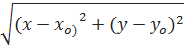 < δ},
< δ},
yo
x0
Определение 3: Окрестностью U точки M0 ϵ ℝn def множество точек, содержащее какую-нибудь её δ-окр-ть.
Определение 4: Точка M def внутренней точкой множества U, если она имеет окрестность, целиком лежащую в этом множестве.
Определение 5: Множество defоткрытым, если оно состоит только из внутренних точек.
Определение 6: Множество def связным, если любые его 2 точки можно соединить принадлежащей ему непрерывной кривой.
Определение 7: Открытое связное множество defобластью.
Определение 8: Точка M def граничной для множества U, если любая её окрестность содержит как точки, принадлежащие множеству, так и точки, не принадлежащие множеству.
Определение 9: Область defодносвязной, если её граница – связное множество.
Определение 10: Множество всех граничных точек множества U def границей множества U (обознач. Fr U, ∂U)
Определение 11: Объединение области и её границы defзамкнутой областью.
§2. Функции. Определение и классификация.
Рассмотрим (∢) множества D и E, ⊂ ℝ
Определение 1: Если каждой (∀) точке xϵD⊂ℝ ставится в соответствие некоторое число y=f(x), yϵE⊂ℝ, то говорят, что на множестве D задана числовая функция f:
Обозначения:
а) y=f(x)
б) f: D Ž E
в) D Ž E
Замечание:
D def ООФ; E def ОЗФ
Примеры:
1. 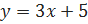

2. 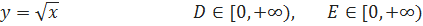
3. 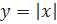
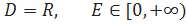
Замечания:
1) Функции С, xn, ax, logax, sinx, cosx, tgx, arcsinx, arccosx, artcgx def простейшими элементарными функциями.
2) Суперпозицией f0 g def сложная функция f(g(x))
3) Функции, полученные из простейших элементарных путём конечного числа арифметических действий или операций суперпозиции, def элементарными функциями.
Примеры:
1) Y = ln (sinx + 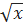 ) – элементарная
) – элементарная
2) y= n! – не элементарная
Способы задания функции:
а) аналитический
б) табличный
в) графический
Классификация по типу:
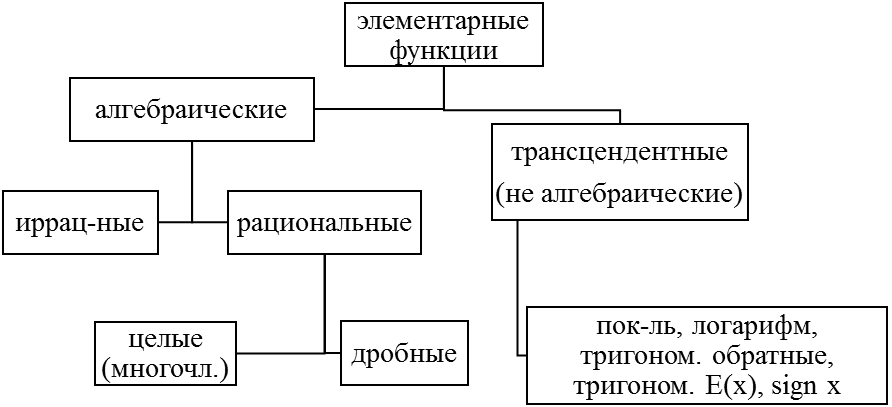
Классификация по свойствам:
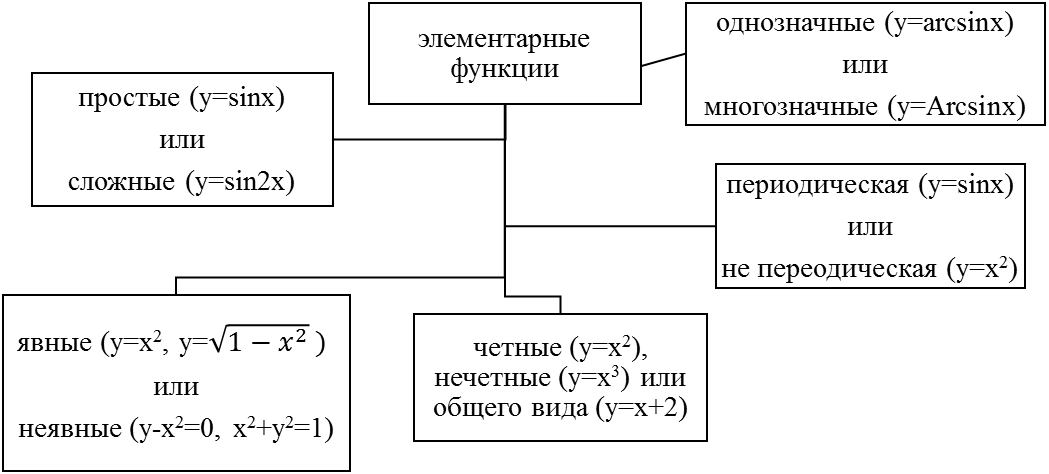
§ 3 Числовая последовательность
Определение 1:Числовой последовательностью x1, x2,…,xn,… def числовая ф-ция натурального аргумента (арг-та) xn=f(n), ∀nϵ ℕ число xn def «n»-ым членом послед-ти.
Примеры: арифметическая и геометрическая последовательности.
Определение 2: Последовательность {xn}n=1 defограниченной, если ∃ (существует) такое число M>0, что для ∀ (любого) nϵ ℕ выполняется неравенство:
|xn|≤M (∀nϵ ℕ)
В противном случае последовательность defнеограниченной.
Определение 3: Последовательность defвозрастающей (неубывающей), если ∀ nϵℕ выполняется неравенство an+1>an [an+1 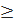 an]
an]
Замечание 1:
Аналогично определяются убывающая и невозрастающая посл-ть.
Замечание 2:
Все эти последовательности defмонотонными.
Определение 4: Число a defпределом числовой последовательности (или точкой сгущения) {xn}, если ∀ ε>0 (для любого положительного эпсилон) ∃ N(ε)ϵℕ (существует некоторое натуральное число N, зависящее от эпсилон): ∀n>N(ε) (такое, что для любого n большего N(ε)) ⇒ |xn-a| < ε
Обозначение: 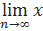 n=a
n=a
Примеры:
Геометрическая иллюстрация определения предела последовательности:
a1 a3 an a-ἐ a a+ἐ a2
Замечание: |xn-a|<ε ⇔ -ε<xn-a<ε ⇒ a-ε<xn<a+ε ⇒ число a – предел посл-ти, если ∀ ε-окр-ти точки a найдётся такое натуральное число N, что начиная с некоторого номера n, все значения xn попадут в ε-окр-ть точки a.
Теорема 1: (о существовании ограниченной последовательности) [теорема Вейерштрасса]
⊐ (пусть) {xn}n=1 – монотонная ограниченная числовая последовательность. Тогда эта последовательность сходится и при этом имеет только один предел.
Пример:
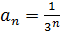 - монотонно убывающая последовательность, т.к.
- монотонно убывающая последовательность, т.к.
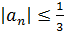 и
и 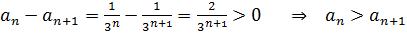
§4. Предел функции
Определение 1: ⊐ функция f(x) определена в некоторой окрестности (.) x0 U(x0)⊂ℝ (за исключением, быть может, самой точки x0). Число a def пределом числовой функции f(x) при xŽx0 (x, стремящийся к x0), если ∀ ε>0 (для любого положительного ε) ∃ δ=δ(ε)>0 (существует положительная дельта, зависящая от ε): ∀ xϵU(x0)=(x0-δ, x0)∪(x0, x0+δ) ⇒ |f(x) – a|<ε
(такая, что для любого x из выколотой δ-окрестности выполняется неравенство |f(x) – a|<ε)
Пример: 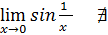 (так как
(так как 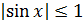 , т.е. синус – функция ограниченная, на всей области определения, колеблющаяся между -1 и 1, то на бесконечности синусоида (косинусоида) не приходит ни к какому определенному значению, следовательно, пределы на бесконечности у этих функций не существуют).
, т.е. синус – функция ограниченная, на всей области определения, колеблющаяся между -1 и 1, то на бесконечности синусоида (косинусоида) не приходит ни к какому определенному значению, следовательно, пределы на бесконечности у этих функций не существуют).
| a |
| x0 |
| X |
Обозначение: 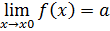 или
или 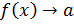
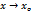
§5. Односторонние пределы
⊐ функция f(x) определена в некоторой окрестности точки x0 (за исключением, быть может, самой (.) x0)
Определение 1: Число a defпределом функции f(x) при xŽx0 слева (справа), если ∀ ε>0: ∃ δ=δ(ε)>0 такое, что ∀ xϵ(x0-δ, x0) [∀ xϵ(x0, x0+δ)] ⇒ |f(x)-a|<ε
Обозначение: 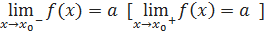
или 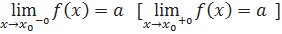
Замечания:
1) Пределы такого рода defодносторонними (соответственно левосторонними или правосторонними)
2) В общем случае пределы слева и справа не равны друг другу.
Теорема 2: (необходимое и достаточное условие существования предела)
Функция 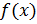 имеет в (.)
имеет в (.) 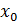 предел тогда и только тогда [т. и т. т.], когда в (.)
предел тогда и только тогда [т. и т. т.], когда в (.) 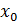 ∃-ют (существуют) пределы этой функции слева и справа, и они равны между собой, т.е.:
∃-ют (существуют) пределы этой функции слева и справа, и они равны между собой, т.е.:
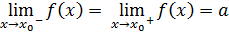
Следствие:
Если пределы слева и справа существуют, но не равны или один из них или оба не существуют (∄), то предел функции 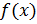 не существует.
не существует.
Примеры:
Y Y
a a1
X a2 X
xo
§6. Пределы на бесконечности. Бесконечные пределы.
∢ (рассмотрим) обобщение понятия предела на случай, когда 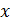 неограничено.
неограничено.
Определение 1: ⊐ ф-ция 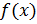 определенна в окрестности бесконечно удалённой точки, т.е. ∀
определенна в окрестности бесконечно удалённой точки, т.е. ∀ 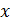 :
: 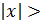 K при некотором K>0. Число
K при некотором K>0. Число 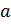 есть предел ф-ции
есть предел ф-ции 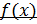 при
при 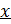 , стремящемся к ∞, если ∀ε>0 ∃δ>K: ∀
, стремящемся к ∞, если ∀ε>0 ∃δ>K: ∀ 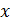 , |
, | 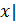 > δ ⇒ |
> δ ⇒ | 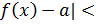 ε
ε
Обозначение:
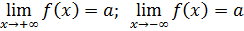
a+ἐ
a
a-ἐ
-KK1 K=K2 δ
K= max {|K1|, |K2|}
Замечание: Частным случаем предела функции на бесконечности является предел последовательности.
Определение 2: ⊐ функция 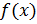 определена в некоторой окрестности точки
определена в некоторой окрестности точки 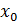 (за исключением, быть может, самой точки
(за исключением, быть может, самой точки 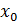 ). Функция
). Функция 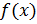 имеет предел
имеет предел 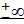 при
при 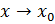 , если ∀ε>0 ∃δ=δ(ε)>0: ∀x: |x-x0|<δ ⇒ |f(x)|
, если ∀ε>0 ∃δ=δ(ε)>0: ∀x: |x-x0|<δ ⇒ |f(x)|
Обозначение: 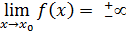
Эти пределы называются бесконечными пределами.
Y
ε
X
xo-δ xo xo+δ
§7. Ограниченные, бесконечно-малые и бесконечно-большие функции.
Определение 1: Функция f(x), определённая в некоторой области U(x0)⊂ℝ, называется ограниченной в этой области, если ∃N>0: ∀x ϵ U(x0) ⇒ |f(x)|≤N
Y
X
a b
Примеры:
1) y=sin x
|sin x|≤1 ∀x ϵ ℝ, т.е. ограничена на всей числовой оси.
2) 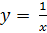 ограничена на [1;2], т.к. ∃ N=1: ∀x ϵ [1;2] ⇒
ограничена на [1;2], т.к. ∃ N=1: ∀x ϵ [1;2] ⇒ 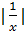 ≤1.
≤1.
Определение 2: Функция α(x), определенная в некоторой окрестности точки x0, ≝ бесконечно-малой, если 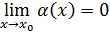 т.е. ∀ε>0 ∃δ=δ(ε)>0: ∀x ϵ U(x0) ⇒ |α(x)|<ε
т.е. ∀ε>0 ∃δ=δ(ε)>0: ∀x ϵ U(x0) ⇒ |α(x)|<ε
Y
0 X
xo
Определение 3: Функция A(x), определенная в некоторой окрестности (.) x0, ≝ бесконечно-большой при xŽx0, если 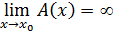 , т.е. ∀ε>0 ∃δ=δ(ε)>0: ∀xϵUδ(x0) ⇒ |f(x)|>ε.
, т.е. ∀ε>0 ∃δ=δ(ε)>0: ∀xϵUδ(x0) ⇒ |f(x)|>ε.
Примеры:
1. 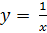 - бесконечно-большая при
- бесконечно-большая при 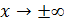 .
.
§8. Теоремы о бесконечно-малых
Теорема 1: 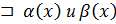 – б/м при
– б/м при 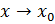
↷(тогда) 1) α(x)+β(x) – б/м при xŽx0; 2) α(x)*β(x) – б/м при xŽx0
Доказательство:
1) 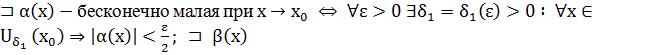
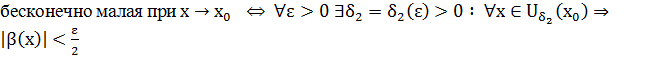
Обозначим через δ=min {δ1,δ2} ↷
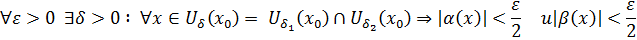
↷ 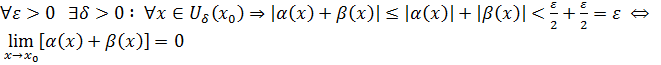
2) Доказывается аналогично, исходя из α(x) – б/м при xŽx0 ⇔ ∀ε>0 ∃δ1>0: ∀xϵ 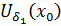 ⇒ |α(x)|<
⇒ |α(x)|< 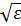 ч.т.д.
ч.т.д.
Теорема 2:
Произведение ограниченной функции на бесконечно малую есть бесконечно малая, т.е. если α(x) – б/м при xŽx0, f(x) – ограниченная в U(x0) функция, то f(x)*α(x) – б/м при xŽx0.
Док-во:
Т.к. f(x) – ограничена в U(x0) ⇒ |f(x)|≤N, т.к. α(x) – б/м при xŽx0 ⇒ ∀ε>0 ∃δ=δ(ε)>0: ∀xϵUδ(x0) ⇒ |α(x)|< 
∢ U(x0) 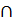 Ug(x0) ↷ ∀xϵU(x0)
Ug(x0) ↷ ∀xϵU(x0) 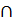 Ug(x0) ⇒ |f(x)*α(x)|=|f(x)|*|α(x)|<N*
Ug(x0) ⇒ |f(x)*α(x)|=|f(x)|*|α(x)|<N* 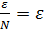 ч.т.д.
ч.т.д.
Теорема 3:
⊐ функция f(x) определена в U(x0). Для того, чтобы
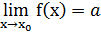 , необходимо и достаточно, чтобы функция
, необходимо и достаточно, чтобы функция 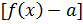 была бесконечно-малой при x→xo.
была бесконечно-малой при x→xo.
Док-во:
1. (необходимость) ⊐ 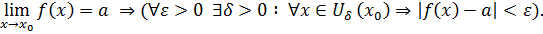 Обозначим через
Обозначим через 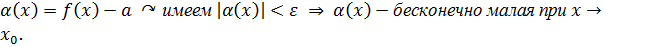
2. (достаточность) ⊐ 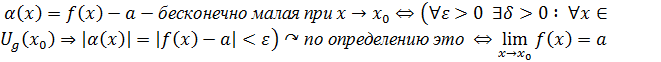
Итак, 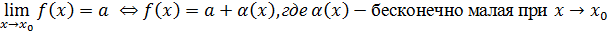
Теорема 4:
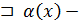 бесконечно малая при
бесконечно малая при 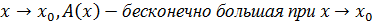 ↷
↷ 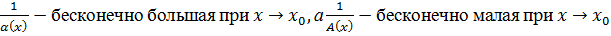
Док-во:
⊐ 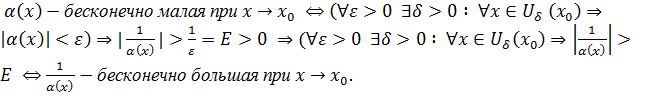
Вторая часть доказывается аналогично.
 2020-09-24
2020-09-24 274
274






