Объём цилиндра и конуса

За величину объёма цилиндра принимается предел, к которому стремится объём правильной призмы, вписанной в цилиндр, когда число боковых граней этой призмы неограниченно удваивается.

За величину объёма конуса (полного или усечённого) принимается предел, к которому стремится объём правильной пирамиды (полной или усечённой), когда число боковых граней пирамиды неограниченно удваивается.

Теоремы.

1) Объём цилиндра равен произведению площади основания на высоту.

2) Объём конуса равен произведению площади основания на треть высоты.

Доказательство:

Впишем в цилиндр какую-нибудь правильную призму, а в конус— какую-нибудь правильную пирамиду; тогда, обозначив площадь основания призмы или пирамиды буквой В₁, высоту их буквой Н и объём — V₁ получим:

для призмы V₁ = В₁Н;

для пирамиды V₁ = ¹/₃В₁Н.

Вообразим теперь, что число боковых граней призмы и пирамиды неограниченно удваивается. Тогда В1 будет иметь пределом площадь В основания цилиндра или конуса, а высота Н остаётся без изменения; значит, произведения В₁Н и ¹/₃ В₁Н будут стремиться к пределам ВН и ¹/₃ВН, и потому объём V цилиндра или конуса будет:

для цилиндра V = ВН;

для конуса V = ¹/₃ ВН. ■

Следствие.

Если радиус основания цилиндра или конуса обозначим через R, то В = πR², поэтому

объём цилиндра V = πR²Н;

объём конуса V = ¹/₃ πR²Н.

 

Теорема. Объём усечённого конуса равен сумме объёмов трёх конусов, имеющих одинаковую высоту с усечённым конусом, а основаниями: один — нижнее основание этого конуса, другой — верхнее, третий— круг, площадь которого есть среднее геометрическое между площадями верхнего и нижнего оснований.

Доказательство самостоятельно (аналогично теореме для объёма усечённой пирамиды).

 

Шар

Тело, получаемое вращением полукруга вокруг диаметра, называется шаром, а поверхность, образуемая при этом полуокружностью, называется шаровой или сферической поверхностью. Можно также сказать, что эта поверхность есть геометрическое место точек, одинаково удалённых от одной и той же точки (называемой центром шара).

Отрезок, соединяющий центр с какой-нибудь точкой поверхности, называется радиусом, а отрезок, соединяющий две точки поверхности и проходящий через центр, называется диаметром шара. Все радиусы одного шара равны между собой; всякий диаметр равен двум радиусам.

Два шара одинакового радиуса равны, потому что при вложении они совмещаются.

Теорема. Всякое сечение шара плоскостью есть круг.

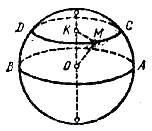
1) Предположим сначала, что секущая плоскость АВ проходит через центр О шара. Все точки линии пересечения принадлежат шаровой поверхности и поэтому одинаково удалены от точки О, лежащей в секущей плоскости; следовательно, сечение есть круг с центром в точке О.

2) Положим теперь, что секущая плоскость СО не проходит через центр. Опустим на неё из центра перпендикуляр OK и возьмём на линии пересечения какую-нибудь точку М. Соединив её с О и А, получим прямоугольный треугольник МОК, из которого находим:

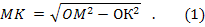
Так как длины отрезков ОМ и ОК не изменяются при изменении положения точки М на линии пересечения, то расстояние МК есть величина постоянная для данного сечения; значит, линия пересечения есть окружность, центр которой есть точка К. ■

Следствия.

Пусть R и r будут длины радиуса шара и радиуса круга сечения, а

  d — расстояние секущей плоскости от центра, тогда равенство (1) примет вид:

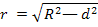
Из этой формулы выводим, что:

1) Наибольший радиус сечения получается при d = 0, т. е. когда секущая плоскость проходит через центр шара. В этом случае r =R. Круг, получаемый в этом случае, называется большим кругом.

2) Наименьший радиус сечения получается при d = R. В этом случае r = 0, т. е. круг сечения обращается в точку.

3) Сечения, равноотстоящие от центра шара, равны.

4) Из двух сечений, неодинаково удалённых от центра шара, то, которое ближе к центру, имеет больший радиус.

 

Теоремы о площади поверхности шара и его объеме примем без доказательства:

Теорема. Поверхность шара равна произведению длины окружности большого круга на диаметр или: поверхность шара равна учетверённой площади большого круга, т.е. S_ш=4πR²

 

Теорема. Объём шара равняется произведению его поверхности на треть радиуса.

 

Теорема. Поверхность и объём шара соответственно составляют 2/3 полной поверхности и объёма цилиндра, описанного около шара.

Доказательство: самостоятельно