21.05.2020
ПЗ № 60. Тригонометрические уравнения
Справочные материалы для выполнения работы
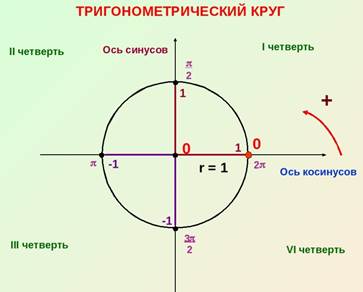
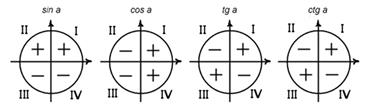
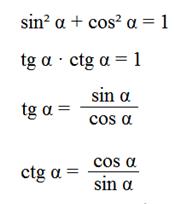
| 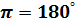 Пример 1.Перевести в градусы
Пример 1.Перевести в градусы 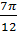 Вместо
Вместо 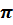 подставляем подставляем 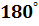 и сокращаем дробь и сокращаем дробь
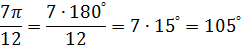 Пример 2. Перевести в радианы
Пример 2. Перевести в радианы 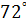 Записываем дробь, в числитель дописываем
Записываем дробь, в числитель дописываем 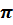 ,в знаменатель записываем ,в знаменатель записываем 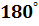 и сокращаем дробь и сокращаем дробь
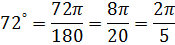 Пример 3.В какой четверти лежит угол
Пример 3.В какой четверти лежит угол 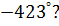 Так как угол со знаком «минус», то откладываем его в противоположную сторону, то есть по часовой стрелке. Полный круг будет (
Так как угол со знаком «минус», то откладываем его в противоположную сторону, то есть по часовой стрелке. Полный круг будет (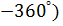 еще добавляем еще добавляем 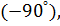 получим нижняя точка получим нижняя точка 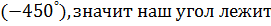
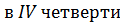 Пример 4.Определить знак
Пример 4.Определить знак 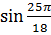 .
Сначала переведите в градусы .
Сначала переведите в градусы 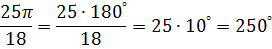 По кругу смотрим, это III четверть. Смотрите в таблице, какой знак имеет синус в III четверти (-). Ответ
По кругу смотрим, это III четверть. Смотрите в таблице, какой знак имеет синус в III четверти (-). Ответ 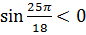
|
При решении простейших тригонометрических уравнений (тестовых заданий с выбором ответа) иногда достаточно знать общий вид формулы для данного уравнения и сверять ее с предложенными ответами (если справа стоит число, отличное от 0, 1 или-1). Если справа в уравнениях с синусом и косинусом стоит 0; 1 или -1, то ответе берем из III и IV столбцов таблицы (Формулы корней)
Формулы корней тригонометрических уравнений.
| Общие | Частные | ||
| Уравнение | Формула корней | Уравнение | Формула корней |
| 1. sinx = a, |a|≤1 | x = (-1)narcsin a + πn, n є Z | 1. sinx = 0 | x = πn, n є Z |
| 2. cosx = a, |a|≤1 | x = ±arccos a + 2πn, n є Z | 2. sinx = 1 | x = 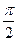 + 2πn, n є Z + 2πn, n є Z
|
| 3. tg x = a | x = arctg a + πn, n є Z | 3. sinx = –1 | x = – 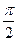 + 2πn, n є Z + 2πn, n є Z
|
| 4. ctg x = a | x = arcctg a + πn, n є Z | 4. cosx = 0 | x = 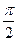 + πn, n є Z + πn, n є Z
|
| 5. cosx = 1 | x = 2πn, n є Z | ||
| 6. cosx = –1 | x = π + 2πn, n є Z | ||
Если уравнение содержит функцию 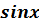
| В формуле корней обязательно будет: 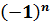 … + … + 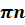 Если справа число отрицательное
Если справа число отрицательное
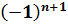 … + … + 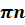
|
Если уравнение содержит функцию 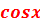
| В формуле корней обязательно будет: 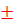 … + … + 
|
Если уравнение содержит функцию 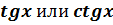
| В формуле корней не должно быть: 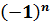 …или …или 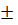 …
Если справа число отрицательное, то ответ будет начинаться со знака «минус» …
Если справа число отрицательное, то ответ будет начинаться со знака «минус»
|
Пример 5. Решите уравнение
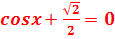
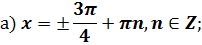
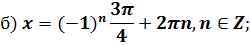
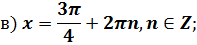
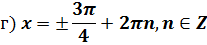
| Если перенести вправо 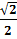 ,то получим уравнение ,то получим уравнение 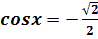
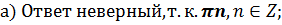
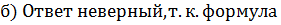
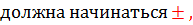
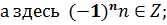
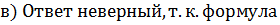
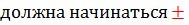
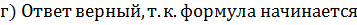
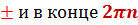
|
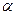
| 0 
| 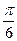
| 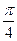
| 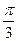
| 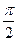
| 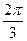
| 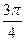
| 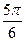
| 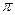
| 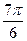
| 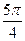
| 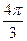
| 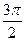
| 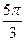
| 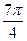
| 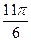
| 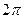
|
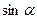
| 0 | 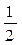
| 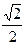
| 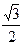
| 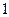
| 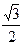
| 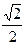
| 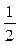
| 0 | 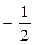
| 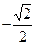
| 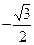
| -1 | 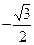
| 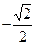
| 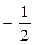
| 0 |
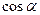
| 1 | 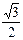
| 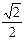
| 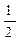
| 0 | 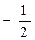
| 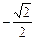
| 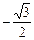
| -1 | 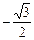
| 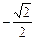
| 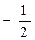
| 0 | 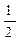
| 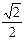
| 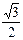
| 1 |
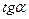
| 0 | 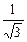
| 1 | 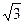
| - | 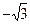
| -1 | 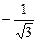
| 0 | 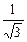
| 1 | 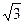
| - | 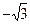
| -1 | 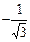
| 0 |
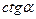
| - | 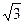
| 1 | 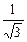
| 0 | 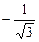
| -1 | 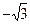
| - | 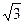
| 1 | 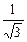
| 0 | 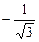
| -1 | 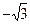
| - |
Выполните тест.
Вариант 1. Первые 12 человек по списку
Вариант 2. Остальные.
В заданиях1-11 выберите только один правильный ответ. В заданиях 1-11 решения записывать не нужно, только букву с правильным ответом. (Задания 7,8,9,10 взяты из экзаменационных работ) Обязательно прикладывайте решение номеров 12, 13 (на оценку 5).
1. Переведите угол 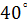 в радианы:
в радианы:
а) 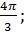 б)
б) 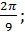 в)
в) 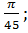 г)
г) 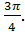
2. Чему равна величина угла 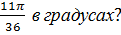
а) 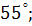 б)
б) 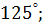 в)
в) 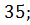 г)
г) 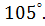
3. В какой четверти расположен угол 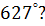
а) 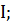 б)
б) 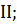 в)
в) 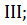 г)
г) 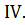
4. В какой четверти расположен угол 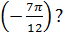
а) 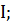 б)
б) 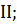 в)
в) 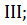 г)
г) 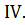
5. Определите знак 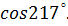
а) 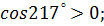 б)
б) 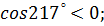 в)
в) 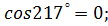 г)
г) 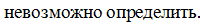
6. Вычислите 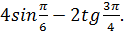
а) 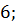 б)
б) 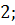 в)
в) 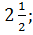 г)
г) 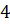
7. Упростите выражение 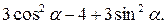
а) -1; б) 5; в) 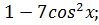 г)
г) 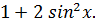
8. Упростите выражение 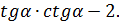
а) 1; б) -2; в) -3; г) -1.
9. Решите уравнение 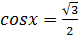 .
.
а) 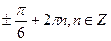 ; б)
; б) 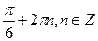 ;
;
в) 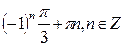 ; г)
; г) 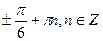 .
.
10. Решите уравнение 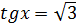
а) 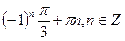 ; б)
; б) 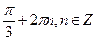 ; в)
; в) 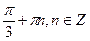 ; г)
; г) 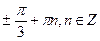 .
.
11. Найдите устно решение уравнения 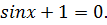
а) 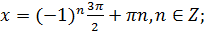 б)
б) 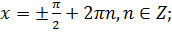
в) 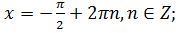 г)
г) 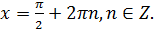
12. 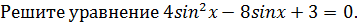
13. 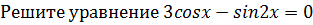 .
.
Вариант 2.
1. Переведите угол 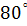 в радианы:
в радианы:
а) 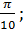 б)
б) 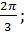 в)
в) 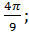 г)
г) 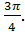
2. Чему равна величина угла 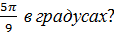
а) 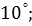 б)
б) 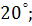 в)
в) 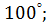 г)
г) 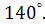
3. В какой четверти расположен угол 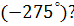
а) 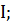 б)
б) 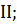 в)
в) 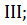 г)
г) 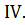
4. В какой четверти расположен угол 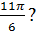
а) 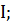 б)
б) 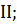 в)
в) 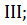 г)
г) 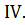
5. Определите знак 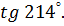
а) 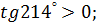 б)
б) 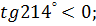 в)
в) 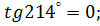 г)
г) 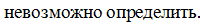
6. Вычислите 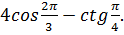
а) 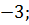 б)
б) 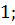 в)
в) 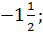 г)
г) 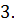
7. Упростите выражение 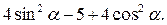
а) 3; б) -1; в) 9; г) 1.
8. Упростите выражение 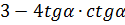
а) 2; б) 3- 4cos2α; в) -1; г) 3-4sin2α.
9. Решите уравнение ctg x=1.
а) 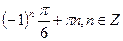 ; б)
; б) 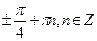 ;
;
в) 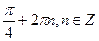 ; г)
; г) 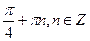 .
.
10. Решите уравнение 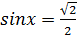 :
:
а) 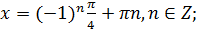 б)
б) 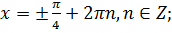
в) 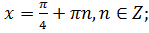 г)
г) 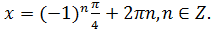
11. Найдите устно решение уравнения 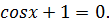
а) 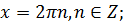 б)
б) 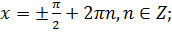
в) 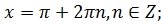 г)
г) 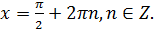
12. 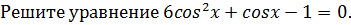
13. 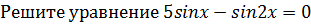 .
.
Критерии оценок:
«3» 6-9 тестовых
«4» 10-11 тестовых
«5» 8-11 тестовых + 12 или 13
 2020-09-24
2020-09-24 174
174






