2020-10-10
1162
Рассмотрим произвольную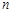 
-членную операцию 
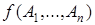, заданную своей таблицы значений, не являющуюся противоречием. Рассмотрим строки таблицы, в которых f принимает значения “1”. Для каждой строки составим элементарные конъюнкции из n множителей, где i -й множитель равен 
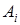(в этой строке 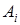принимает значение “1”) или 
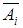(в этой строке 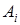принимает значение “0”). Далее возьмем дизъюнкцию всех полученных конъюнкций. В итоге получится формула (ДНФ), задающая операцию, равносильную 
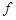. Действительно, каждая из построенных конъюнкций будет истинна только при тех значениях истинности высказываний 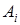, которые стоят в соответствующей строчке. Поскольку была взята дизъюнкция по всем наборам значений истинности высказываний 
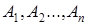, на которых 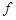истинна, то построенное высказывание истинно на всех этих наборах и только на них. На остальных наборах оно ложно.
Построенная формула называется совершенной дизъюнктивной нормальной формой (СДНФ) операции .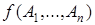
Определение 2.1. СДНФ (совершенная ДНФ) – это такая ДНФ, в которой каждая элементарная конъюнкция содержит все элементарные высказывания, либо их отрицания по одному разу, элементарные конъюнкции не повторяются.
|
|
|
Пример.
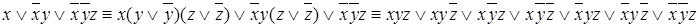
Аналогично, рассматривая строки, в которых операция 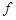, не являющаяся тавтологией, принимает значения “0”, и составляя конъюнкцию (число множителей равно числу отмеченных строк таблицы) дизъюнкций из n слагаемых, где i -е слагаемое равно 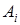(в этой строке 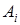принимает значение “0”) или 
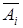(в этой строке 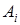принимает значение “1”). В итоге получится формула, задающая операцию, равносильную 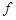. Построенная формула называется совершенной конъюнктивной нормальной формой (СКНФ) операции .
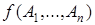Определение 2.2. СКНФ (совершенная КНФ) – это такая КНФ, в которой каждая элементарная дизъюнкция содержит все элементарные высказывания, либо их отрицания по одному разу, элементарные дизъюнкции не повторяются.
Пример.
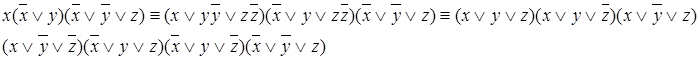
Каждая формула имеет одну единственную СДНФ и одну единственную СКНФ. Тавтология не имеет СКНФ, а противоречие – СДНФ.
Как известно, каждая формула логики высказываний представляет некоторую булеву функцию. Возникает обратный вопрос: можно ли всякую булеву функцию представить некоторой формулой логики высказываний? Можно указать алгоритм, который позволяет по таблице истинности произвольной булевой функции от любого числа переменных построить некоторую формулу логики высказываний в СДНФ.
Пример.
Рассмотрим частный случай. Пусть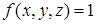 
только в одном единственном случае.
| x | y | z | f(x,y,z) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
Тогда этой формуле будет соответствовать функция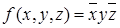 
.
|
|
|
Если рассматривать произвольную функцию, то необходимо выделить все наборы переменных, для которых функция принимает значение 1 и каждому набору поставить в соответствие конъюнкцию переменных и их отрицаний. Рассматриваемая функция будет представлена дизъюнкцией этих конъюнкций.
Таким образом, установлена процедура, которая позволяет для всякой булевой функции записать соответствующую ей формулу.
Пример.
| x | y | z | f(x,y,z) |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
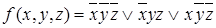
Теорема 2.3. Каждую булеву функцию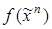 
при любом 
(
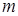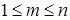) можно представить в виде
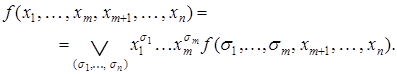(2.1)
Это представление называется разложением функции по переменным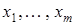 
.
Доказательство. Заметим, что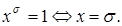 
Далее рассмотрим произвольный набор 
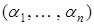и покажем, что левая и правая часть формулы (2.1) принимают на нем одно и то же значение.
Левая часть дает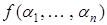 
, а правая
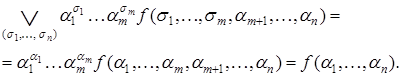
Следствие 1. Разложение по переменной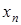 
. Пусть 
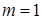. Тогда
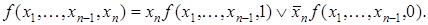
Следствие 2. Разложение по всем переменным. Пусть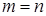 
. Тогда
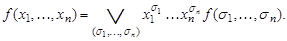
При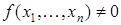 
получаем выражение
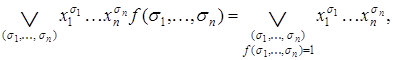
т.е.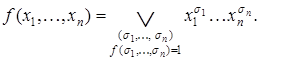 
(2.2)
Разложение (2.2) носит название совершенной дизъюнктивной нормальной формы (СДНФ).
Замечания: 1. Поскольку существует взаимно однозначное соответствие между таблицей истинности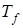 
и СДНФ функции 
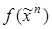, то СДНФ функции единственна.
2. Единственная функция, не имеющая СДНФ, – константа 0.
3. Длина СДНФ функции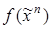 
равна числу наборов, на которых функция принимает значение, равное 1.
Теорема 2.4. Каждую булеву функцию 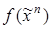при любом 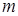(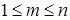) можно представить в виде
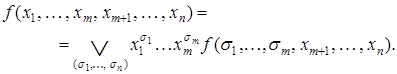(2.3)
Это представление называется разложением функции по переменным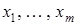 
.
Доказательство. Заметим, что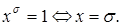 
Далее рассмотрим произвольный набор 
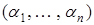и покажем, что левая и правая часть формулы (2.3) принимают на нем одно и то же значение.
Левая часть дает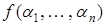 
, а правая
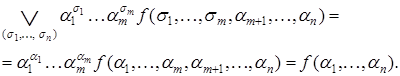
Следствие 1. Разложение по переменной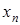 
. Пусть 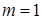. Тогда
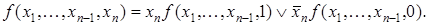
Следствие 2. Разложение по всем переменным. Пусть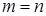 
. Тогда
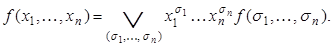
При 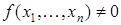получаем выражение
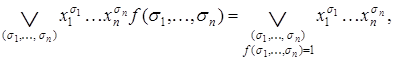
т.е. 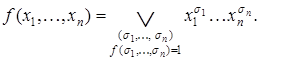(2.4)
Разложение (2.4) носит название совершенной дизъюнктивной нормальной формы (СДНФ).
Замечания: 1. Поскольку существует взаимно однозначное соответствие между таблицей истинности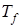 
и СКНФ функции 
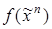, то СКНФ функции единственна.
2. Единственная функция, не имеющая СКНФ, – константа 1.
3. Длина СКНФ функции 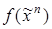равна числу наборов, на которых функция принимает значение, равное 0.
Утверждение 2.1. Отрицание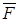 
всякой формулы 
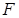алгебры высказываний равно дизъюнкции тех и только тех совершенных конъюнктивных одночленов, которые не входят в СДН-формы формулы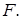 
Утверждение 2.2. Отрицание 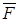всякой формулы 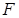алгебры высказываний равно конъюнкции тех и только тех совершенных дизъюнктивных одночленов, которые не входят в СКН-формы формулы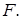
Утверждение 2.3. Для нахождения отрицания произвольной формулы, составленной из пропозициональных переменных и операций конъюнкция, дизъюнкция и отрицание, достаточно всюду заменить знак операции «конъюнкция» на знак операции «дизъюнкция», а знак операции «дизъюнкция» заменить на знак операции «конъюнкция» и всякую переменную входящую в формулу без знака отрицания, заменить на ту же переменную с инверсией, а все имеющиеся знаки отрицания убрать.
Пример. Найти отрицание формулы: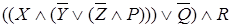 
Руководствуясь утверждением 2.3, выпишем отрицание для формулы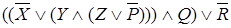 
.
Пример. Перейдите от СДНФ к СКНФ:
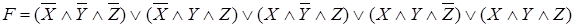.Согласно утверждению 2.1 имеем: отрицание формулы имеет следующую СДНФ: 
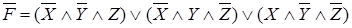.Теперь применяя утверждение 2.3, находим отрицание этой формулы 
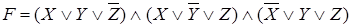. Это и есть СКНФ данной формулы.
Пример. Перейдите от СКНФ к СДНФ: 
. Согласно утверждению 2.2 имеем: отрицание формулы имеет следующую СКНФ: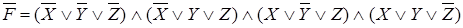 
. Теперь применяя утверждение 2.3, находим отрицание этой формулы 
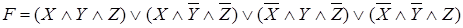. Это и есть СКНФ данной формулы.
|
|
|
А теперь сформулируем основные определения и понятия, касающиеся нормальных и совершенных форм.
Вернемся к понятию конъюнкта и дизъюнкта. Конъюнкции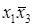 
, 
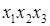, 1 являются элементарными. Причем первая элементарная конъюнкция имеет ранг (число литералов) 2, вторая - 3, а третья - 0. Дизъюнкции 
, 
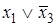, 1 являются элементарными. Причем первая элементарная дизъюнкция имеет ранг (число литералов) 2, вторая - 3, а третья - 0.
Следующие дизъюнкции: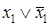 
, 
, 
, 
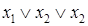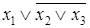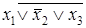, 0 не являются элементарными.
Определение 2.3. Элементарная конъюнкция булевой функции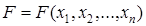 
содержащая n литералов, называется полной (или min-термом). Элементарная дизъюнкция булевой функции 
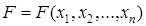, содержащая n литералов, называется полной (max-термом).
Определение 2.4. Число элементарных конъюнкций (слагаемых, термов), составляющих ДНФ, называется длиной ДНФ. Число элементарных дизъюнкций, составляющих КНФ, называется длиной КНФ.
Пример. Определить длину данной ДНФ и КНФ. ДНФ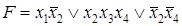 
имеет длину, равную 3. КНФ 
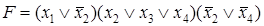имеет длину, равную 3.
Определение 2.5. Две (или несколько) ДНФ, реализующих одну и ту же булеву функцию F, называются эквивалентными (или равносильными). Две (или несколько) КНФ, реализующих одну и ту же булеву функцию F, называются эквивалентными (или равносильными).
