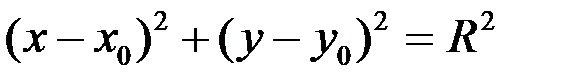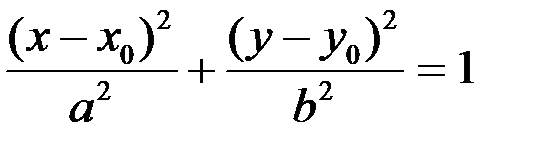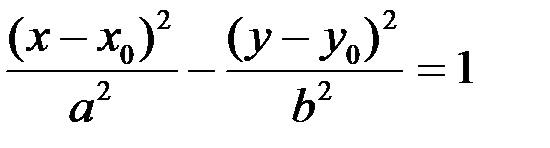Кривыми второго порядка называются линии, которые описываются алгебраическими уравнениями второй степени
Ax 2 + B xy + C y2 + Dx + Ey + F = 0, (1.15)
причем хотя бы один из коэффициентов А, B, С должен быть не равен нулю.
Окружностью называется геометрическое место точек равноудаленных от данной точки, называемой центром окружности. Уравнение окружности радиуса R с центром в точке M (а, b) имеет вид
(x - a)2 + (y - b)2 = R 2. (1.16)
Если a = b = 0,то центр окружности лежит в начеле координат. Такая окружность называется канонической x 2 + y 2 = R 2. Если раскрыть скобки, то мы увидим, что уравнение (1.16) получается из уравнения (1.15), если
A = C = 1, B = 0, D = -2 a, E = -2 b, F = - R 2 + a 2 + b 2.
Пример. Пусть задано уравнение х 2 + y 2 - 4 x = 0. Является ли это уравнение уравнением окружности и, если да, то каков ее радиус и координаты центра?
Решение. Попробуем привести данное уравнение к виду (1.16). Для этого выделим полный квадрат относительно х, прибавляя и вычитая число 4
x 2 + y 2 - 4 x = (x 2 - 4 x + 4) + y 2 - 4 = 0
или
(x - 2)2 + y 2 = 22. (1.17)
Сравнивая (1.16) с (1.17), видим, что заданное уравнение есть уравнение окружности радиусом R = 2 и с центром в точке M (2, 0).
Эллипс - замкнутая кривая, для всех точек которой сумма расстояний до двух фиксированных точек F 1 и F 2, называемых фокусами эллипса, есть величина постоянная (т.е. одинакова) и равна, по определению, 2 а (а > 0).
Если центр симметрии эллипса находится в начале координат, а фокусы F 1 (с, 0) и F 2 (- с, 0) лежат на оси ОХ (рис.1.14), то такое расположение называется каноническим. Точка М – текущая точка эллипса. Сумма расстояний MF 1 и MF 2 равна, по определению, 2 а.
MF 1 + MF 2 = 2 а,
и, так как
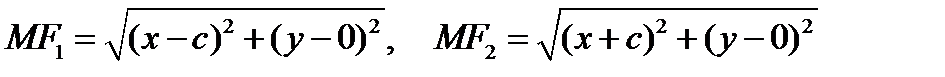 ,
,
то получим
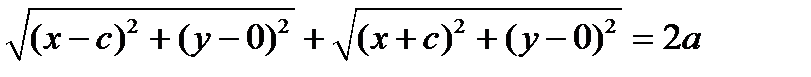 .
.
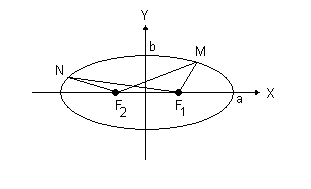
Рис.4.14. Канонический эллипс. MF 1 + MF 2 = NF 1 + NF 2 = 2 а,
Преобразуя это уравнение, получим уравнение эллипса, которое называется каноническим
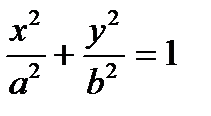 . (1.18)
. (1.18)
Величины a и b называются малой и большой полуосью эллипса (величины 2 а и 2 b называются осями, величины a, b, с – параметры эллипса), причем
a 2 = b 2+ c 2.
Отношение 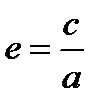 называется эксцентриситетом, эксцентриситет эллипса меньше единицы е < 1.
называется эксцентриситетом, эксцентриситет эллипса меньше единицы е < 1.
Уравнение (1.18) получим из (1.16) если
B = D = E = 0, 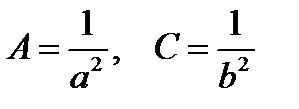 , F = -1.
, F = -1.
Очевидно, что окружность - частный случай эллипса, у которого a = b = R, а центр находится в начале координат.
Гипербола – неограниченная кривая, для всех точек которой разность расстояний до двух фиксированных точек, называемых фокусами, есть величина постоянная и по определению равна 2 а (рис. 1.15). Если центр симметрии гиперболы находится в начале координат, а фокусы F 1 (с, 0) и F 2 (- с, 0) лежат на оси ОХ (рис.1.15), то такое расположение называется каноническим. Точка М – текущая точка гиперболы. Разность расстояний MF 1 и MF2 равна, по определению, 2 а (а > 0).
MF 2 – MF 1 = 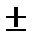 2 а.
2 а.
Знак 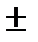 необходим, так как разность расстояний может иметь любой знак. Здесь, так же как и для эллипса
необходим, так как разность расстояний может иметь любой знак. Здесь, так же как и для эллипса
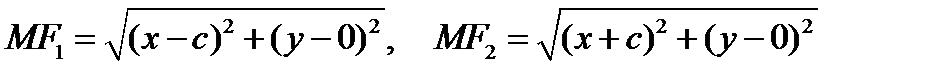 .
.
Отсюда
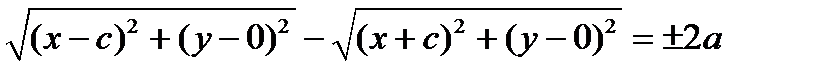 .
.
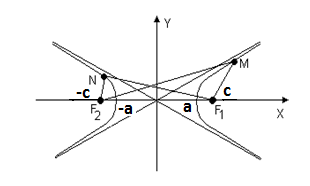
Рис. 1.15. Каноническая гипербола. MF2 – MF1 = NF1 – NF2 = 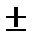 2а.
2а.
Проведя преобразования, получим каноническое уравнение гиперболы
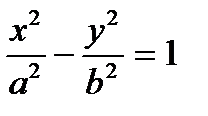 . (1.19)
. (1.19)
Параметры а и b называются полуосью и мнимой полуосью гиперболы (величины a, b, с – параметры гиперболы), причем, в отличии от эллипса,
c 2 = b 2 + a 2.
Эксцентриситет гиперболы 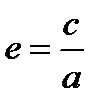 больше единицы e > 1.
больше единицы e > 1.
Уравнение (1.19) получим из (1.15) если
B = D = E = 0, 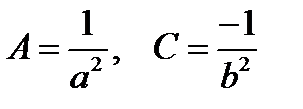 , F = - 1.
, F = - 1.
Особенность гиперболы – наличие наклонных асимптот - прямых к которым неограниченно приближается кривая при 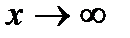 . Уравнения асимптот
. Уравнения асимптот
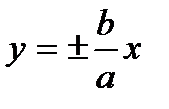 .
.
Парабола - неограниченная кривая, все точки которой (рис. 1.16) равноудалены от точки, называемой фокусом и прямой, называемой директрисой, причем расстояние между фокусом и директрисой равно р. Если фокус F лежит на оси ОХ в точке с координатами F (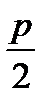 ,0), а уравнение директрисы
,0), а уравнение директрисы 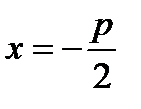 , и директриса перпендикулярна оси ОХ, то парабола называется канонической. Точка М (x, y) – текущая точка параболы. Точка К лежит на директрисе и имеет координаы
, и директриса перпендикулярна оси ОХ, то парабола называется канонической. Точка М (x, y) – текущая точка параболы. Точка К лежит на директрисе и имеет координаы 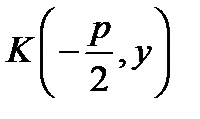 . По определению MK = MF.
. По определению MK = MF.
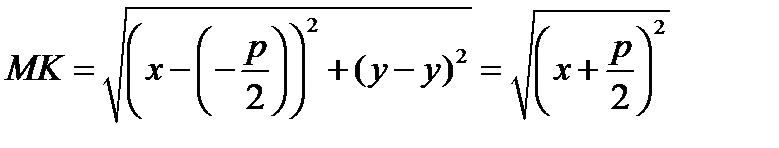
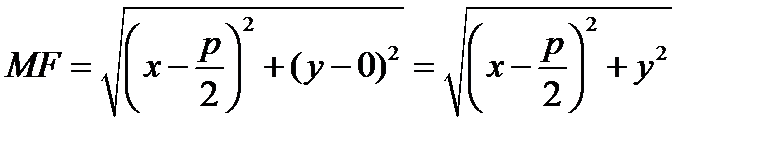
Или, по определению
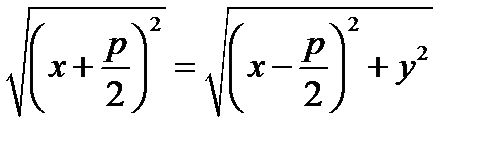
Возводя в квадрат и приводя подобные члены, получим каноническое уравнение параболы
y 2 = 2 px. (1.20)
Величина р называется параметром параболы, ось ОХ – ось параболы. Уравнение (1.20) получим из (1.15) если
A = B = E = F = 0, C = 1, D = - 2 p.
Сделав поворот и сдвиг системы координат, любое уравнение (1.15) можно привести только к одному из трех уравнений второй степени: (1.18), (1.19), (1.20) или к уравнению вида 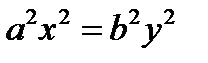 , которому соответствуют две прямые, проходящие через начало координат. Это означает, что уравнениями второй степени можно описать только эллипс (и его частный случай окружность), гиперболу или параболу.
, которому соответствуют две прямые, проходящие через начало координат. Это означает, что уравнениями второй степени можно описать только эллипс (и его частный случай окружность), гиперболу или параболу.
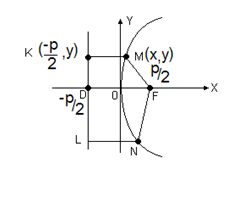
Рис. 1.16. Каноническая парабола. NF = NL и MK = MF
Ниже приведены канонические уравнения кривых второго порядка с центром симметрии (в случае параболы – вершиной) в начале координат (случай А) и в точке С (x 0, y 0) (случай В).
А В
| Окружность | 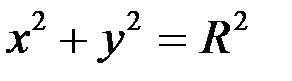
|
| |
| Эллипс | 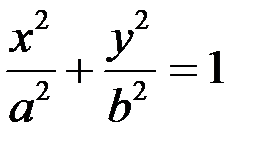
|
| |
| Гипербола | 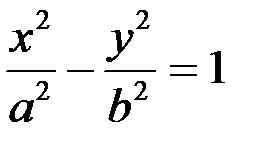
|
| |
| Парабола | 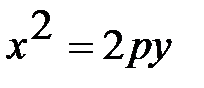
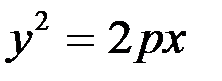
| 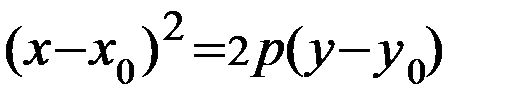 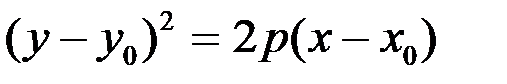
| |
 2020-10-10
2020-10-10 172
172