Составление матрицы планирования ДФЭ
Для построения матрицы планирования ДФЭ из имеющихся n факторов отбирают (n-p) основных факторов, для которых строят МП ПФЭ. Эту матрицу дополняют затем p столбцами, соответствующими оставшимся факторам. Уровни дополнительных факторов определяют как поэлементное умножение уровней не менее двух и не более (n-p) основных факторов. Говорят, что ДФЭ – это эксперимент типа 2n-p.
Выбранное для дополнительного фактора произведение называется генератором плана. ДФЭ типа 2n-p будет иметь p генераторов.
Например, для ДФЭ типа 23-1 число опытов равно 4 опытам, по сравнению с 16 опытами в случае ПФЭ (таблица 1). При трех основных факторах ДФЭ содержит 8 опытов, а генератором для дробных планов может служить произведение  .
.
Таблица 1
| № | x1 | x2 | x3=x1x2 |
| 1 | - | - | + |
| 2 | + | - | - |
| 3 | - | + | - |
| 4 | + | + | + |
При введении одного дополнительного фактора (ДФЭ типа 24-1) может использоваться любой из четырех возможных генераторов: x4=x1x2, x4=x1x3, x4=x2x3, x4=x1x2x3.
Порядок постановки ДФЭ
Проводят К опытов, в результате получают значения yi1, yi2,…, y1k. Для них находят среднее значение. Затем проводят проверку воспроизводимости опытов (однородности дисперсий) по формуле:

Гипотезу однородности (равенства) дисперсий проверяют с помощью критерия Корхена:

Его критическое значение находят из таблицы распределения Корхена по числу степеней свободы числителя f=K-1, знаменателя f=N и уровню значимости. Если расчетное значение больше критического, то гипотеза об однородности принимается, иначе – отвергается и эксперимент требуется повторить, изменив условия его проведения.
Расчет оценок коэффициентов регрессионного уравнения

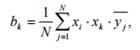

Проверка значимости коэффициентов регрессии
Проверка осуществляется по критерию Стьюдента. Сравниваются расчетное значение критерия и его критическое значение из таблицы распределения Стьюдента. Если расчетное значение критерия больше критического, то коэффициент значимый.
Проверка адекватности полученной ММ
Адекватность ММ проверяется по критерию Фишера. Если расчетное значение больше критического (находят по таблице распределения Фишера), то гипотеза об адекватности отклоняется. Сперва проверяют адекватность линейной ММ. Если предположение об адекватности подтверждается, то в качестве окончательной ММ выбирают линейную; если отклоняется – добавляют эффект взаимодействия с небольшим коэффициентом и вновь проверяют гипотезу, и так до тех пор, пока существуют степени свободы. Для насыщенного и сверхнасыщенного экспериментов проверка на адекватность невозможна, т.к. для нее уже не останется степеней свободы.
6. Факторный анализ.
Факторы можно разделить на три группы:
1) группа постоянных или случайно изменяющихся в ходе исследования факторов W, значения которых известны;
2) группа управляемых факторов U, значения которых целенаправленно изменяются в ходе эксперимента (две первых группы обычно объединяют в одну группу X контролируемых параметров);
3) группа неконтролируемых параметров Z, значения которых остаются неизвестными в ходе исследования.
Зависимость величины отклика от контролируемых факторов называется функцией отклика. Геометрическое представление функции отклика называется поверхностью отклика. Чтобы такое представление стало возможным, вводится понятие факторного пространства, у которого координатные оси соответствуют отдельным факторам.
Любая точка факторного пространства характеризуется набором значений факторов, при котором производится измерение отклика. Фиксированное значение фактора называют уровнем фактора. При количестве факторов, большем трех, геометрическое представление факторного пространства становится невозможным. Поэтому чаще всего множество уровней факторов, при которых производится измерение отклика, задается матрицей условий эксперимента. Эта матрица для k факторов и N измерений имеет вид
 .
.
Значения отклика, полученные при данных измерениях, также представляется матрицей, которая имеет один столбец и называется матрицей наблюдений:
 .
.
7. Полный факторный эксперимент.
Первый этап планирования эксперимента для получения линейной модели основан на варьировании факторов на двух уровнях. В этом случае, если число факторов известно, можно сразу найти число опытов, необходимое для реализации всех возможных сочетаний уровней факторов.
Интервалом варьирования факторов называется некоторое число (свое для каждого фактора), прибавление которого к основному уровню дает верхний, а вычитание – нижний уровни фактора. Другими словами, интервал варьирования – это расстояние на координатной оси между основным и верхним (или нижним) уровнем.
Формула, которая для этого используется: 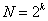 , где N – число опытов, k – число факторов, 2 – число уровней. В общем случае эксперимент, в котором реализуются всевозможные сочетания уровней факторов, называется полным факторным экспериментом. Если число уровней каждого фактора равно двум, то имеем полный факторный эксперимент типа 2 k.
, где N – число опытов, k – число факторов, 2 – число уровней. В общем случае эксперимент, в котором реализуются всевозможные сочетания уровней факторов, называется полным факторным экспериментом. Если число уровней каждого фактора равно двум, то имеем полный факторный эксперимент типа 2 k.
Матрица планирования для двух факторов приведена ниже
| № опыта | x 1 | x 2 | y |
| 1 | –1 | –1 | y1 |
| 2 | +1 | –1 | y2 |
| 3 | –1 | +1 | y3 |
| 4 | +1 | +1 | y4 |
Каждый столбец в матрице планирования называют вектор-столбцом, а каждую строку – вектор-строкой. Таким образом, мы имеем 2 вектор-столбца независимых переменных и один вектор-столбец параметра оптимизации.
Квадратичный полином:
 .
.
Достоинством данного метода можно считать высокую точность при рассчитывании опытов, доскональное исследование.
Недостатком является большие затраты на исследование, емкость расчетов.
8. Планирование и организация проведения эксперимента.
Планирование эксперимента позволяет минимизировать время, особенно в случае воздействия нескольких различных факторов на конечный результат опыта, и расход материальных ресурсов.
Планирование и организация эксперимента предусматривает
- выбор числа варьируемых факторов. Здесь необходимо выбирать наиболее значимые переменные, которые оказывают влияние на функцию отклика. Определить их можно в ходе выполнения предварительных поисковых экспериментов, обзора литературных источников;
- определение числа уровней каждого варьируемого фактора. В данном случае определяется либо качественное либо количественное значение уровня, которое к тому же может быть фиксированным либо случайным. Каких-то определенных рекомендаций по нахождению интервала изменения факторов не существует, поэтому в данном пункте стоит обратиться к литературным источникам, чтобы определить возможные интервалы изменения фактора, либо воспользоваться своим личным опытом;
- определение необходимого числа измерений значения функции отклика. Данное количество зависит от установленных ограничений, требуемой точности и возможного влияния одного фактора на другой.
Эксперименты различаются:
а) степенью воздействия на изучаемый объект - активный, пассивный;
б) организацией проведения - лабораторный, натурный;
в) характером взаимодействия с объектом исследования - материальный (классический), вычислительный, мыслительный;
г) ожидаемым результатом - качественный, количественный;
д) числом варьируемых факторов - однофакторный, многофакторный;
е) природой изучаемого объекта или явления - физический, экономический, социометрический, технологический и др.
Критерии достоверности результатов эмпирического исследования должны удовлетворять, в частности, следующим признакам:
Критерии должны быть объективными настолько, на - сколько это возможно в данной научной области), позволять оценивать исследуемый признак однозначно, не допускать спорных оценок разными людьми.
Критерии должны быть адекватными, валидными, то есть оценивать именно то, что исследователь хочет оценить.
Критерии должны быть нейтральными по отношению к исследуемым явлением. Так, если в ходе педагогического эксперимента учащимися в одних классах, допустим, изучается какая-то новая тема, а в других – нет, то в качестве критерия сравнения нельзя брать знание учащимися материала этой темы.
Совокупность критериев с достаточной полнотой должна охватывать все существенные характеристики исследуемого явления, процесса.
9. Корреляционный анализ.
Корреляционный анализ - метод, позволяющий обнаружить зависимость между несколькими случайными величинами.
Методами корреляционного анализа решаются следующие задачи:
· Взаимосвязь. Есть ли взаимосвязь между параметрами?
· Прогнозирование. Если известно поведение одного параметра, то можно предсказать поведение другого параметра, коррелирующего с первым.
· Классификация и идентификация объектов. Корреляционный анализ помогает подобрать набор независимых признаков для классификации.
Допустим, проводится независимое измерение различных параметров у одного типа объектов. Из этих данных можно получить качественно новую информацию – о взаимосвязи этих параметров.
Например, измеряем рост и вес человека, каждое измерение представлено точкой в двумерном пространстве:

Несмотря на то, что величины носят случайный характер, в общем наблюдается некоторая зависимость - величины коррелируют.
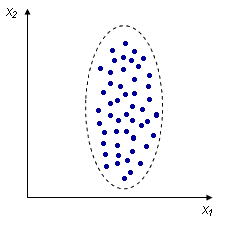
В данном случае это положительная корреляция (при увеличении одного параметра второй тоже увеличивается). Возможны также такие случаи:
Отрицательная корреляция:

| Отсутствие корреляции:
|
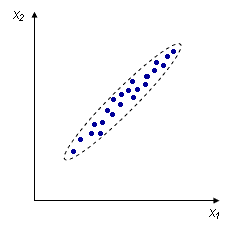
Взаимосвязь между переменными необходимо охарактеризовать численно, чтобы, например, различать такие случаи:

| 
|
10. Случайные величины и параметры их распределений.
Основные причины, определяющие надёжность изделия, связаны со случайными явлениями, для описания которых применяется математический аппарат теории вероятностей.
Например:
отказ – это случайное событие;
срок службы или наработка до отказа – случайная величина и процесс;
потеря работоспособности (например, изнашивание), - случайная функция.
Поэтому в расчетах надежности многие параметры должны рассматриваться как случайные величины, т.е. такие, которые могут принять то или иное значение, неизвестное заранее.
Случайные события.
Событие называют возможным или случайным, если в результате опыта оно может произойти или не произойти.
Вероятность события – есть численная мера степени объективной возможности появления этого события.
Невозможным называется событие, которое не может произойти в условиях данного опыта.
Частота события - статистическая вероятность события - отношение числа появления данного события к числу всех произведённых опытов.
Случайные величины.
Случайной называется величина, которая в результате опыта может принимать то или иное значение, неизвестное заранее, какое именно.
Дискретной (прерывной) случайной величиной называется случайная величина, принимающая отделенные друг от друга значения (число отказавших изделий при испытаниях заданного объёма).
Непрерывной случайной величиной называется случайная величина, возможные значения которой непрерывно заполняют какой-то промежуток (время работы изделия до отказа).
11. Законы распределения случайных величин.
Законом распределения случайной величины называется соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Закон распределения может иметь разные формы.
1. Функция распределения случайной величины X этофункция F(x), выражающая вероятность того, что X примет значение, меньшее, чем х:
F(x) = P(X<x).
Функция F(x) есть неубывающая функция (монотонно возрастающая для непрерывных процессов и ступенчато возрастающая для дискретных процессов);
2. Плотность распределения случайной величины это функция
f(x) = dF(x)/dx = F'(x).
Функция f(x) характеризует частость повторений данного значения случайной величины.
Числовые характеристики случайных величин.
Основными числовыми характеристиками случайной величины являются, среднее арифметическое (выборочное среднее), среднее квадратическое отклонение и коэффициент вариации.
12. Нормальный закон распределения.
Непрерывная случайная величина t называется нормально распределенной, если ее плотность вероятности имеет следующий вид

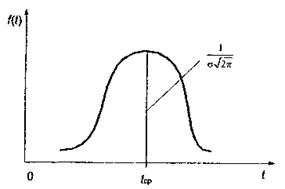 |
где tср, s - параметры нормального распределения (математическое ожидание и среднее квадратическое отклонение).
Рис. Нормальное распределение
Параметр tcp характеризует положение распределения на оси абсцисс, а параметр s форму кривой.
Для упрощения вычислений при решении практических задач надежности прибегают к центрированию и нормированию нормального распределения.
Под центрированием понимается перенос центра группирования случайной величины tcp в начало координат, тогда tcp = 0, а среднее квадратическое отклонение s = 1. Если ввести новую переменную, то такая операция называется нормированием.

В результате центрирования и нормирования получим новое распределение случайной величины z:

Функция f0(z) является однопараметрической, и ее значения приведены в таблицах нормального распределения. При отрицательных значениях z функция f(-z) = f(z). После того как найдены значения fo(z), необходимо перейти обратно к функции f(t):
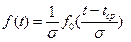
Вероятность безотказной работы до возникновения первого отказа вычисляется из выражения

где  - функция Лапласа, значения которой приведены в таблицах математической статистики. Эта функция нечетная, т.е. при Ф(- z) = - Ф(z)
- функция Лапласа, значения которой приведены в таблицах математической статистики. Эта функция нечетная, т.е. при Ф(- z) = - Ф(z)
Вероятность отказа определяется по формуле
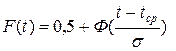
Нормальный закон распределения хорошо описывает процессы, на которые влияют большое число независимых факторов, каждый из которых оказывает незначительное воздействие. Ему подчиняются износные отказы, ресурсы агрегатов и отдельных деталей, люфты и зазоры в сочленениях, трудоемкости обслуживания и др.
13. Оценивание с помощью доверительного интервала.
Наиболее информативный способ оценивания значений исследуемых откликов Y = f(X) состоит не только в определении их точечных статистических параметров  и sx2, а в построении интервала, в котором с заданной степенью достоверности окажется оцениваемый отклик.
и sx2, а в построении интервала, в котором с заданной степенью достоверности окажется оцениваемый отклик.
Интервальной оценкой отклика Y называется интервал, границы которого 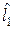 и
и  , является функциями значений x1, x2..., xN и который с заданной вероятностью p накрывает оцениваемый отклик Y:
, является функциями значений x1, x2..., xN и который с заданной вероятностью p накрывает оцениваемый отклик Y:
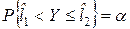 .
.
Интервал  называется доверительным, а его границы
называется доверительным, а его границы  и
и  - соответственно нижним и верхним доверительными пределами, вероятность
- соответственно нижним и верхним доверительными пределами, вероятность  – доверительной вероятностью, используемым при построении доверительного интервала. Тогда любая интегральная оценка может быть охарактеризована совокупностью двух величин: шириной доверительного интервала
– доверительной вероятностью, используемым при построении доверительного интервала. Тогда любая интегральная оценка может быть охарактеризована совокупностью двух величин: шириной доверительного интервала  , являющегося мерой точности оценивания отклика Y, и доверительной вероятностью
, являющегося мерой точности оценивания отклика Y, и доверительной вероятностью  , характеризующей степень достоверности (надежности) результатов. Практически чаще всего используется значение
, характеризующей степень достоверности (надежности) результатов. Практически чаще всего используется значение  = 0,95, несколько реже
= 0,95, несколько реже  = 0,90 и
= 0,90 и  = 0,99 и совсем редко
= 0,99 и совсем редко  = 0,8 и
= 0,8 и  = 0,999.
= 0,999.
Для построения доверительных интервалов для среднего значения  мощности привода по строкам, когда
мощности привода по строкам, когда  неизвестна, используется формула:
неизвестна, используется формула:
 ,
,
где 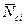 - средние значения мощности по строкам;
- средние значения мощности по строкам;  - среднее квадратическое отклонение по строке;
- среднее квадратическое отклонение по строке;
Численные значения t – распределения Стьюдента приведены в Приложении
14. Статистические гипотезы.
На разных этапах статистического исследования возникает необходимость в формулировании и экспериментальной проверке некоторых предположительных утверждений – гипотез.
Статистической называют гипотезу о виде неизвестного распределения или о параметрах известных распределений.
Выдвигается основная (нулевая) гипотеза Н0 и проверяется, не противоречит ли она имеющимся эмпирическим данным. Конкурирующей (альтернативной) называют гипотезу Н1, которая противоречит нулевой.
В результате статистической проверки гипотезы могут быть допущены ошибки двух родов. Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза; вероятность совершить такую ошибку обозначают  и называют ее уровнем значимости. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза, вероятность которой обозначают
и называют ее уровнем значимости. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза, вероятность которой обозначают  , а мощностью критерия является вероятность
, а мощностью критерия является вероятность 
Логическая схема построения проверки гипотез

Сравнение двух дисперсий нормальных генеральных совокупностей.

Сравнение двух средних нормальных генеральных совокупностей с известными дисперсиями.
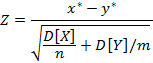
Сравнение выборочной средней с гипотетической генеральной средней нормальной совокупности.

Сравнение наблюдаемой относительной частоты с гипотетической вероятностью появления события.

15. Отсев грубых погрешностей.
На практике, как правило, число измерений конечно и в большинстве случаев не превышает 15–30. При таком малом числе наблюдений мы можем определить только оценки математического ожидания Мx и дисперсии sx, т.е. рассчитать 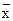 и Sx. Измерения при малом числе наблюдений чаще всего дают меньшее значение среднеквадратичной погрешности Sx по сравнению с погрешностью для достаточно большого ряда тех же измерений (в пределе всей генеральной совокупности) sx. Поэтому при неизвестных действительных значениях Мx, sx, ограниченном числе испытаний, используют распределение Стьюдента и довольствуются весьма приближенными методами. При распределении Стьюдента вероятность появления, например, одинаково больших погрешностей в распределении Стьюдента, т.е. при малом числе измерений, больше.
и Sx. Измерения при малом числе наблюдений чаще всего дают меньшее значение среднеквадратичной погрешности Sx по сравнению с погрешностью для достаточно большого ряда тех же измерений (в пределе всей генеральной совокупности) sx. Поэтому при неизвестных действительных значениях Мx, sx, ограниченном числе испытаний, используют распределение Стьюдента и довольствуются весьма приближенными методами. При распределении Стьюдента вероятность появления, например, одинаково больших погрешностей в распределении Стьюдента, т.е. при малом числе измерений, больше.
Рассмотрим случайную величину t, равную отношению случайной величины  и Sx
и Sx
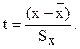 (3.9)
(3.9)
При этом предполагается, что случайная величина 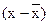 распределена по нормальному закону. Если обозначить вероятность появления того или иного значения t в пределах
распределена по нормальному закону. Если обозначить вероятность появления того или иного значения t в пределах 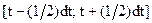 через f(t)dt, то плотность распределения вероятности появления величины t имеет вид:
через f(t)dt, то плотность распределения вероятности появления величины t имеет вид:
 (3.10)
(3.10)
Это распределение названо распределением Стьюдента. Здесь Г(x) – гамма-функция, являющаяся обобщением понятия факториала и обладающая рекуррентным свойством: 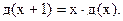 Для целых чисел n справедливо
Для целых чисел n справедливо  Множители при
Множители при  в f(t) выбраны так, чтобы площадь под любой кривой f(t) равнялась единице.
в f(t) выбраны так, чтобы площадь под любой кривой f(t) равнялась единице.
На рис. 1. приведено распределение Стьюдента для различных значений n. При n®¥ (практически при n³30) распределение Стьюдента переходит в нормальное распределение с единичной дисперсией. Распределение Стьюдента позволяет оценить величину надежности Р по заданному значению 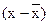 или, наоборот, по заданной величине надежности (доверительной вероятности) найти величину погрешности результата
или, наоборот, по заданной величине надежности (доверительной вероятности) найти величину погрешности результата 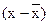 .
.
Действительно, если взять на оси t некоторое значение ta,n, то величина надежности будет определяться площадью, ограниченной осью t, ординатами -ta и +ta и кривой f(t). Следовательно, при недостаточно большом числе измерений (n³30) при расчете  при заданном уровне надежности Р, необходимо вводить вместо коэффициента e(a), коэффициент Стьюдента ta,n.
при заданном уровне надежности Р, необходимо вводить вместо коэффициента e(a), коэффициент Стьюдента ta,n.
Процедура отсева грубых погрешностей измерений заключается в следующем:
1. По результатам наблюдений (измерений) и объему выборки n рассчитываются оценки математического ожидания  и дисперсии Sx2.
и дисперсии Sx2.

Рис.1. Кривая t-распределения Стьюдента
2. Из всего ряда наблюдений выбирается наблюдение (измерение), имеющее наибольшее отклонение от среднеарифметического значения xmax.
3. Формулируется нуль-гипотеза Н0: отклонение xmax от  несущественно с доверительной вероятностью Р (уровнем значимости a).
несущественно с доверительной вероятностью Р (уровнем значимости a).
4. Для оценки этой гипотезы рассчитывается максимальное относительное (по отношению к среднеквадратичному) отклонение:
 (3.11)
(3.11)
где xmax – "выскакивающее" значение.
5. В качестве критерия проверки статистической нуль-гипотезы используется теоретическое значение критерия Стьюдента t, которое зависит от уровня значимости a или доверительной вероятности P=1-a. ta,m=n-1 – представляет собой допустимое отклонение случайной величины, выраженное в долях оценки среднеквадратичного отклонения и учитывает ограниченность объема выборки (n) и заданную доверительную вероятность (P). Данные ta,m для различных значений a представлены в справочной литературе. При наличии современных ПЭВМ можно воспользоваться пакетами прикладных программ или интегрированными средами, например, электронными таблицами Microsoft Excel.
6. Если tэксп>ta,m, то имеется достаточно основания с вероятностью P исключить "выскакивающее" значение как грубую ошибку и отвергнуть нуль-гипотезу. В противном случае tэксп<ta,m, нуль гипотеза Н0 принимается и от отсева "выскакивающего значения" лучше воздержаться с вероятностью P.
16. Характеристики случайной величины.
Среднее арифметическое случайной величины характеризует центр группирования всей совокупности ее значений

где Xi - центр i -ro интервала вариационного ряда; m - соответствующая данному интервалу частота; к - количество интервалов вариационного ряда; и n - объем выборки.
Среднее квадратическое отклонение случайной величины s (х), характеризующет меру рассеивания значений X вокруг центра группирования  . Определяют по формуле
. Определяют по формуле

Коэффициент вариации ряда - оценивает относительную меру рассеивания случайной величины X и в первом приближении позволяет судить о законе ее распределения

Чем меньше значение коэффициента вариации, тем плотнее группируются результаты испытаний вокруг среднего значения  , тем, следовательно, меньше их рассеивание.
, тем, следовательно, меньше их рассеивание.
17. Экспоненциальный закон распределения.
Непрерывная случайная величина t называется распределенной по экспоненциальному закону, если ее плотность вероятности определяется выражением
 при t > 0
при t > 0
где λ - параметр закона распределения; t- случайная величина наработки,

Рис.. Экспоненциальное распределение
В общем случае экспоненциальным распределением описываются события, которые возникают с постоянной интенсивностью (λ. = const) и независимо друг от друга.
Вероятность безотказной работы P(t) и вероятность отказа F(t) на интервале наработки от 0 до t вычисляются из выражений:

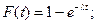
Средняя наработка до отказа (средний ресурс)
 .
.
Среднее квадратическое отклонение для экспоненциального закона распределения

Коэффициент вариации

18. Логарифмически нормальное распределение.
Непрерывная случайная величина t называется распределенной по логарифмически нормальному закону, если логарифм этой величины распределяется по нормальному закону. Плотность распределения имеет вид

 |
Рис. Логарифмически нормальное распределение
где y о математическое ожидание логарифма случайной величины; sл-среднее квадратическое отклонение логарифма случайной величины.


Параметры yо и sл связаны с математическим ожиданием tcp и средним квадратическим отклонением s случайной величины t следующими соотношениями

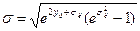
при решении практических задач определения показателей надежности плотность распределения вероятности логарифма t определяется по формуле

где f0(z) - плотность вероятностинормированного распределения.
Вероятность безотказной работы и вероятность отказа находятся из
выражений:
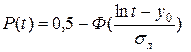
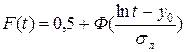
19. Обработка статистических данных.
Для построения закона распределения случайной величины (ресурса t) необходимо провести следующую процедуру.
1) расставить в порядке возрастания значения случайной величины;
2) проверить в случае необходимости полученный ряд на выпадающие (ошибочные) точки, не соответствующие закону распределения. Приближенную проверку проводят по правилу  следующим образом. От полученного среднего значения
следующим образом. От полученного среднего значения 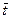 последовательно вычитают и прибавляют
последовательно вычитают и прибавляют  . Если крайние точки ряда не выходят за пределы, то все точки ряда считаются действительными. В противном случае исключают подозрительную точку.
. Если крайние точки ряда не выходят за пределы, то все точки ряда считаются действительными. В противном случае исключают подозрительную точку.
3) построить интервальный вариационный ряд:
а) определяются границы рассеивания, т.е. наибольшее tтax и наименьшее tтin, значения. Разность между ними является размахом варьирования

Далее устанавливается количество интервалов к, на которое необходимо разбить размах R. Число к должно быть не менее

где N - объем выборки испытаний.
Находится ширина интервала вариационного ряда

б) определяются границы интервалов, для чего вначале устанавливается нулевое (крайнее) значение интервала
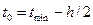
Следующие границы интервалов рассчитываются последовательным прибавлением ширины интервала h к предыдущему значению, т.е.



в) сгруппировать результаты наблюдений. В интервал включаются данные, большие нижней границы интервала или равные ей и меньшие верхней границы. По каждому интервалу подсчитываются середина интервала 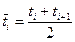 и частота попадания
и частота попадания 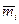 (опытная частота) t в i -й интервал. Все результаты представляются в виде таблицы:
(опытная частота) t в i -й интервал. Все результаты представляются в виде таблицы:
Таблица 1
| Номер интервала | Границы интервалов | Середины интервалов | Частота попадания в интервал |
4) по данным таблицы строится гистограмма. Для её построения в прямоугольной системе координат по оси абсцисс откладывают отрезки, изображающие интервал варьирования, и на этих отрезках, как на основании, строят прямоугольники с высотами, равными частотам соответствующего интервала. В результате получают ступенчатую фигуру, состоящую из прямоугольников, которую и называют гистограммой.
20. Степенные зависимости.
Зависимость степенного вида имеет следующую форму:
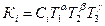 ,
,
где К – показатель качества;
T1, T2, T3, – технологические факторы;
Сi, α, β,γ – коэффициент и показатели степени.
Для определения численных значений коэффициента и показателей степени необходимо провести эксперимент по заданному плану. Необходимо провести варьирование каждого технологического фактора на трех уровнях. Матрица проведения эксперимента позволяет осуществить все возможные сочетания входных факторов.
Для проведения расчетов, значения показателей качества, полученные в каждом опыте, логарифмируются и обозначаются как  .
.
Для построения степенной зависимости необходимо рассчитать значения промежуточных коэффициентов θ0, θ1, θ2, θ3 следующим образом для матрицы с числом опытов равным 12.
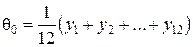



Значения степенных показателей определяется как
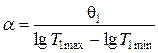

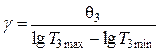
Для определения коэффициента С используется выражение

По полученной эмпирической зависимости строятся однофакторные графики и осуществляется их анализ.
 2020-10-10
2020-10-10 307
307






