Номер: 6.1.В
Задача: Вычислить предел функции 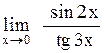
Ответы: 1). 2/3 2). 0 3). 3/2 4). 1 5). 4/9
Номер: 6.3.В
Задача: Вычислить предел функции 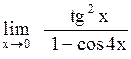
Ответы: 1). 1/8 2). 8 3). 1 4). 0 5). нет правильного ответа
Номер: 6.4.В
Задача: Вычислить предел функции 
Ответы: 1). 0 2). 1 3).  4). 0 5). нет правильного ответа
4). 0 5). нет правильного ответа
Номер: 6.8.В
Задача: Вычислить предел функции 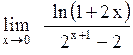
Ответы: 1). 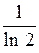 2).
2). 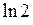 3). 1/2 4). 2 5). 1
3). 1/2 4). 2 5). 1
Номер: 6.11.В
Задача: Вычислить предел функции 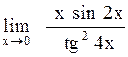
Ответы: 1). 1/8 2). 8 3). – 4 4). 0 5). 1/4
Номер: 6.15.В
Задача: Вычислить предел функции 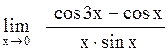
Ответы: 1). 1/8 2). 8 3). – 4 4). 0 5). ¼
Номер: 6.18.В
Задача: Вычислить предел функции 
Ответы: 1). 1 2). 4 3). 0 4). 1/4 5). 
Номер: 6.28.В
Задача: Вычислить предел функции 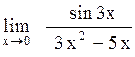
Ответы: 1). – 0,6 2). 0 3). 6/10 4). 1 5). нет правильного ответа
Номер: 6.33.С
Задача: Вычислить предел функции 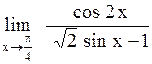
Ответы: 1). -1/2 2). -2 3). 1 4). -1 5). 0
Номер: 6.35.С
Задача: Вычислить предел функции 
Ответы: 1). 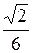 2).
2).  3).
3). 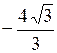 4).
4). 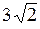 5). 0
5). 0
Номер: 6.41.С
Задача: Вычислить предел 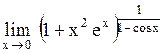
Ответы: 1). 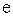 2).
2).  3).
3).  4). 0 5). 1
4). 0 5). 1
Номер: 6.53.С
Задача: Вычислить предел 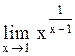
Ответы: 1). 1 2). 0 3).  4).
4). 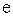 5).
5). 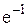
Номер: 6.62.С
Задача: Вычислить предел 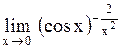
Ответы: 1). 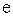 2). 1 3).
2). 1 3).  4).
4). 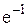 5). 0
5). 0
Номер: 6.78.С
Задача: Используя замечательные пределы, найти те значения  , при которых справедливы приведенные равенства
, при которых справедливы приведенные равенства 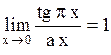
Ответы: 1). 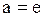 2).
2). 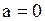 3).
3). 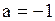 4).
4). 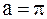 5). нет правильного ответа
5). нет правильного ответа
Номер: 6.83.С
Задача: В указанном множестве найти бесконечно малые при 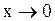 функции
функции 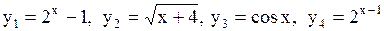
Ответы: 1). 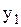 2).
2). 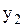 3).
3).  4).
4). 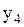 5). нет правильного ответа
5). нет правильного ответа
Номер: 6.85.С
Задача: Используя определения и свойства бесконечно малых в точке функций, вычислите предел 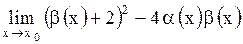 (через
(через 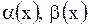 обозначены бесконечно малые в точке
обозначены бесконечно малые в точке 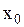 функции).
функции).
Ответы: 1).  2). 0 3). 2 4). -5 5). нет правильного ответа
2). 0 3). 2 4). -5 5). нет правильного ответа
Номер: 6.91.В
Задача: Вычислить предел функции 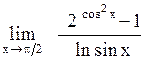
Ответы: 1). 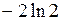 2).
2). 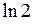 3).
3).  4). 1 5).
4). 1 5). 
Номер: 6.104.В
Задача: Определить порядок относительно  функции, бесконечно малой при
функции, бесконечно малой при 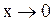
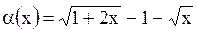 .
.
Ответы: 1). эквивалентные 2). бесконечно малая высшего порядка
3). бесконечно малая более низкого порядка
4). одного порядка, 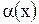 имеет порядок 2
имеет порядок 2
5). одного порядка, 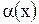 имеет порядок 1/2
имеет порядок 1/2
Номер: 6.105.В
Задача: Определить порядок относительно  функции, бесконечно малой при
функции, бесконечно малой при 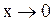
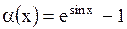 .
.
Ответы: 1). эквивалентные 2). бесконечно малая более высокого порядка
3). бесконечно малая более низкого порядка
4). нет правильного ответа
5). бесконечно малая одного порядка, порядок 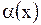 равен 1/2
равен 1/2
Номер: 6.113.А
Задача: Среди следующих определений неверные выделить:
1) б.м.в. 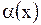 и
и 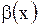 называются б.м.в. одного порядка при
называются б.м.в. одного порядка при 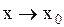 , если отношение
, если отношение  имеет при
имеет при 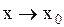 , отличный от нуля предел;
, отличный от нуля предел;
2) б.м.в. одного порядка 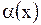 и
и 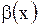 называются эквивалентными при
называются эквивалентными при 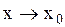 , если
, если 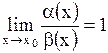 ;
;
3) 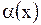 называется б.м.в. более высокого порядка, чем
называется б.м.в. более высокого порядка, чем 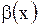 , если
, если 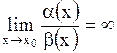 ;
;
4) если 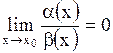 , то
, то 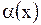 называется б.м.в. более высокого порядка, чем
называется б.м.в. более высокого порядка, чем 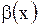 ;
;
5) Если 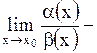 не существует, то
не существует, то 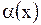 называется б.м.в. более низкого порядка, чем
называется б.м.в. более низкого порядка, чем 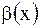 .
.
Ответы: 1). 4 2). 3 3). 4;5 4). все верные 5). 5;3
 2020-10-10
2020-10-10 170
170






