Рабочий лист.
| Предмет | Математика |
| Группа | № 1 2 курс |
| Тема урока | Векторное уравнение прямой и плоскости. |
| ФИО преподавателя | Тимиршина Алия Мунзиловна |
| Где находится задание: | |
| Учебник | М.И. Башмаков Математика, задачник, 2017г |
| Ссылка | http://www.belgtis.ru/images/obuch/pm/MatematikaZadachnikBashmakov.pdf |
| Сроки выполнения задания | 01.10.2020 до 17:00 |
| Как выполнять задание | Написать конспект и выполнить домашнее задание. |
| Домашняя работа | М.И. Башмаков Математика, задачник, 2017г, стр.106 № 5.32 (5,6). |
| Обратная связь | Выполненные работы отправить личным сообщением ВК |
| Как узнать отметку о выполненном задании | Оценки будут выставлены в личный журнал преподавателя и отправлены в беседу ВК. |
Тема: Векторное уравнение прямой и плоскости.
Векторный и координатный метод решения заключается во введении (привязке к исследуемым фигурам) декартовой системы координат, а затем – исчислении образующихся векторов (их длин и углов между ними)
- Расстояние от точки до прямой, не содержащей эту точку, есть длина отрезка перпендикуляра, проведенного из этой точки на прямую.
- Расстояние между двумя параллельными прямыми равно длине отрезка их общего перпендикуляра;
- Расстояние между параллельными прямыми равно расстоянию от любой точки одной из этих прямых до другой прямой;
- Расстояние от точки до плоскости, не содержащей эту точку, есть длина отрезка перпендикуляра, опущенного из этой точки на плоскость;
- Расстояние между прямой и параллельной ей плоскостью равно длине их общего перпендикуляра (расстояние от любой точки прямой до указанной плоскости);
- Расстояние между двумя параллельными плоскостями равно длине их общего перпендикуляра (расстояние между точкой одной из этих плоскостей и другой плоскостью);
- Углом между двумя пересекающимися прямыми называется наименьший из углов, образованных при пересечении прямых, образованных при пересечении прямых (0º <
 < 90º);
< 90º); - Углом между двумя скрещивающимися прямыми, называется угол между двумя пересекающимися прямыми, соответственно параллельными данным скрещивающимся;
- Две прямые называются перпендикулярными, если угол между ними равен 90º;
- Угол между двумя параллельными прямыми считается равным нулю;
- Углом между плоскостью и не перпендикулярной ей прямой называется угол межу этой прямой и ее проекцией на данную плоскость (0º <
 < 90º);
< 90º); - Угол между взаимно перпендикулярными прямой и плоскостью равен 90º;
- Если прямая параллельна плоскости (или лежит в ней ), то угол между ними считается равным 0º;
- Двугранный угол, образованный двумя полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярно его ребру, величина двугранного угла принадлежит промежутку (0º;180º);
- Величина угла между двумя пересекающимися плоскостями принадлежит промежутку
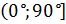 ;
; - Угол между двумя параллельными плоскостями считается равным нулю.
- Ax+By+Cz+D=0 - уравнение плоскости, где
 вектор нормали данной плоскости;
вектор нормали данной плоскости; - A(x-x0 )+B(y-y0 )+C(z-z0 )+D=0 – уравнение плоскости, проходящей через точку M(
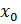 ,
, 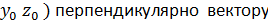
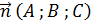 ;
; -
 - длина вектора
- длина вектора  ;
; -
 длина вектора
длина вектора 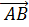 или длина отрезка AB,если A
или длина отрезка AB,если A 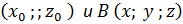
-
 - уравнение плоскости
- уравнение плоскости  M(
M(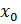 ;
; 
-
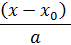 =
= 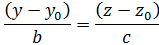 - каноническое уравнение прямой, проходящей через точку M(
- каноническое уравнение прямой, проходящей через точку M(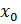 ,
, 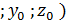 и направляющим вектором
и направляющим вектором  прямой l;
прямой l; - x= x0+a1t, y=y0+a2t, z=z0=a3t – параметрическое уравнение прямой, проходящей через точку M(
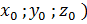 параллельно вектору
параллельно вектору

-
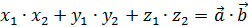 – скалярное произведение векторов
– скалярное произведение векторов 
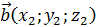 ;
; -
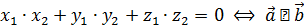 (условие перпендикулярности двух векторов);
(условие перпендикулярности двух векторов); -
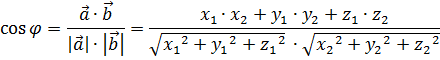 - угол между векторами
- угол между векторами  ;
; -
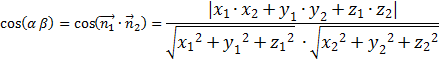 - угол между плоскостями
- угол между плоскостями 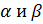 ,
,  и
и 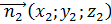 - векторы, перпендикулярные данным плоскостям;
- векторы, перпендикулярные данным плоскостям; - угол между прямыми в пространстве есть острый угол между направляющими векторами данных прямых (прямая однозначно задается точкой и направляющим вектором данной прямой);
- угол между прямой и плоскостью определяется как угол между прямой и проекцией прямой на плоскость. Для нахождения этого угла используется угол между направляющим вектором прямой
 и вектором нормали
и вектором нормали 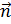 (перпендикулярным) плоскости
(перпендикулярным) плоскости 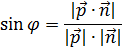 ;
;
Примеры и разбор решения заданий тренировочного модуля
№1. На диагоналях АВ1 и ВС1 граней AA1B1B и ВВ1С1С параллелепипеда ABCDA1B1C1D1 взяты точки соответственно Н и M так, что отрезки MН и A1C параллельны. Найдите отношение длин этих отрезков.
Решение.
Введем векторы: 

Тройку 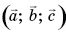 некомпланарных векторов
некомпланарных векторов 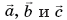 примем в качестве базиса и разложим векторы
примем в качестве базиса и разложим векторы 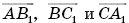 по векторам этого базиса. Имеем:
по векторам этого базиса. Имеем:
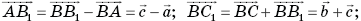

Так как точка Н лежит на диагонали АВ1, то векторы 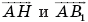 коллинеарны, поэтому существует такое число х, что
коллинеарны, поэтому существует такое число х, что 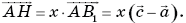 Аналогично, в силу коллинеарности векторов
Аналогично, в силу коллинеарности векторов  существует такое число у, что
существует такое число у, что 
По правилу ломаной находим:
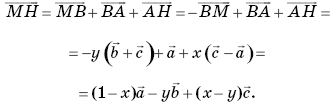
По условию MН  A1C, значит, существует такое число t, что
A1C, значит, существует такое число t, что 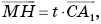 то есть выполняется равенство:
то есть выполняется равенство:
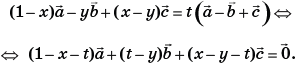
Вследствие некомпланарности векторов  и единственности разложения вектора по базису, приходим к выводу: 1 – х – t = 0, t – у = 0, х – у – t = 0. Решением этой системы уравнений является:
и единственности разложения вектора по базису, приходим к выводу: 1 – х – t = 0, t – у = 0, х – у – t = 0. Решением этой системы уравнений является: 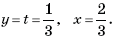 Тогда
Тогда 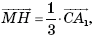 значит, МН: СА1 = 1: 3.
значит, МН: СА1 = 1: 3.
Ответ: 1: 3.
№2 В правильной четырехугольной пирамиде SABCD сторона основания AB= 16,а высота равна 4. На ребрах AB,CD,AS отмечены точки M, N и K соответственно, причем AM = DN = 4,AK = 3.Найдите расстояние от точки K до плоскости SBC.
Решение:

Во введенной прямоугольной системе координат центр основания пирамиды совпадает с началом координат О(0;0;0) вершины имеют координаты:
S(0;0;4),A(0; - 8 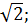 0), B(8
0), B(8 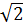 ;0;0),C(0;8
;0;0),C(0;8 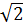 ;0)и D(0;- 8
;0)и D(0;- 8 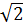 ;0).
;0).
Определим координаты точки K  По условию AK= 3, то точка K делит отрезок AS в отношении
По условию AK= 3, то точка K делит отрезок AS в отношении  :
:
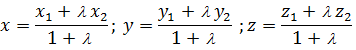 - координаты точки K, где координаты концов отрезка AS
- координаты точки K, где координаты концов отрезка AS 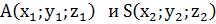 AK: KS= 3: 9=1: 3 (
AK: KS= 3: 9=1: 3 ( SOA по теореме Пифагора SA =
SOA по теореме Пифагора SA = 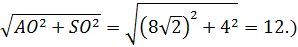
Таким образом, 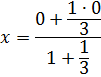 = 0
= 0  ; z=
; z= 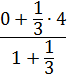 =1⇒ K(0
=1⇒ K(0  1).
1).
Составим уравнение плоскости  , причем воспользуемся другим способом задания уравнения плоскости, отличным от предыдущего. Так как плоскость проходит через точки S (0;0;4), B(8
, причем воспользуемся другим способом задания уравнения плоскости, отличным от предыдущего. Так как плоскость проходит через точки S (0;0;4), B(8 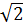 ;0;0)и C(0;8
;0;0)и C(0;8 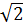 ;0) то подставив координаты точек в общее уравнение плоскости Ax+By + Cz + D = 0, получим систему из трех уравнений:
;0) то подставив координаты точек в общее уравнение плоскости Ax+By + Cz + D = 0, получим систему из трех уравнений:
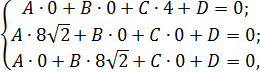 ⟺
⟺ 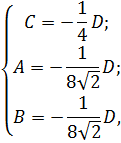 ⟺
⟺
⟺ 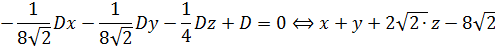
=0- уравнение плоскости (SBC), 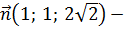 вектор нормали к плоскости.
вектор нормали к плоскости.
Расстояние от точки K до плоскости  :
: 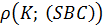 =
= 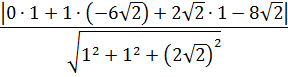 =
= 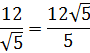 .
.
Ответ: 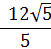 .
.
№3 В кубе ABCDA1B1C1D1, ребро которого равно 6, найдите
(φ- угол между диагональю ВА1 грани АА1В1В и плоскостью ВС1D, А1М- расстояние от вершины А1 до плоскости ВС1D)
1. V=?
2. А1М=?
3. φ=?
Решение:
1. Объем куба равен кубу его стороны, значит
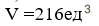
2)Пусть отрезок A1М — перпендикуляр из вершины А1 на (ВС1D), М 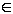 (ВС1D) (рис. 4). Тогда A1М = ρ(А1; (ВС1D)). Найдем длину отрезка A1М.
(ВС1D) (рис. 4). Тогда A1М = ρ(А1; (ВС1D)). Найдем длину отрезка A1М.
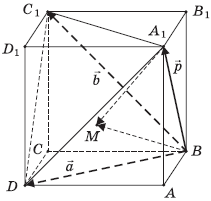
По правилу треугольника имеем: 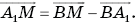
Обозначим: 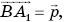 а в плоскости ВС1D введем базис
а в плоскости ВС1D введем базис  где
где 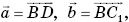 и запишем разложение вектора
и запишем разложение вектора 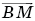 по векторам этого базиса в виде:
по векторам этого базиса в виде:  Тогда
Тогда 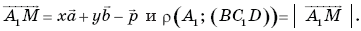
Так как A1М 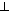 (ВС1D), то A1М
(ВС1D), то A1М 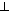 ВС1, A1М
ВС1, A1М 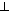 ВD (по определению прямой, перпендикулярной плоскости), значит,
ВD (по определению прямой, перпендикулярной плоскости), значит, 
Коэффициенты х и у в разложении 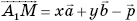 вектора
вектора 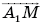 найдем, пользуясь условием:
найдем, пользуясь условием: 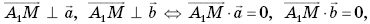
которое равносильно системе уравнений

Прежде чем решать эту систему уравнений, найдем скалярные произведения векторов:
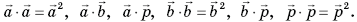
Так как треугольники ВС1D, A1ВС1, A1ВDv— правильные и равные, то длины их сторон равны 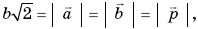 а
а 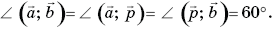
Тогда:
 (**)
(**)
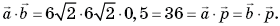 (***)
(***)
Вернемся к решению системы уравнений (*).
Учитывая соотношения (**) и (***) и свойства скалярного произведения векторов, получаем:

Тогда 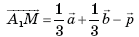 и
и
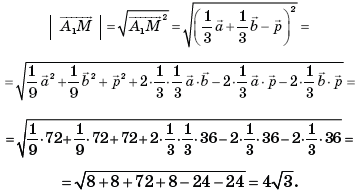
Таким образом, 
3)Обозначим 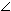 (ВА1; (ВС1D)) = φ. Так как А1М
(ВА1; (ВС1D)) = φ. Так как А1М 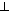 (ВС1D), то ВМ — ортогональная проекция ВС1 на (ВС1D)
(ВС1D), то ВМ — ортогональная проекция ВС1 на (ВС1D)
значит, 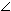 (ВА1; (ВС1D)) =
(ВА1; (ВС1D)) = 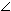 (ВА1; ВМ)=
(ВА1; ВМ)=  =
= 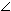 А1ВМ = φ.
А1ВМ = φ.
Используя соотношения (**) и (***) и то, что вектор 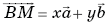 при
при 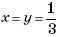 имеет вид
имеет вид  находим:
находим:

Ответ:
1) 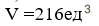
2)А1М=4√3
3) φ= arccos√(3/3)
Домашнее задание: М.И. Башмаков Математика, задачник, 2017г, стр.106 № 5.32 (5,6).
 2020-10-11
2020-10-11 172
172






