1.Различные определения вектора, характеристики вектора.
Определение 1. Геометрический отрезок называется ориентированным, если указан порядок его концов.
Определение 2. Вектором (геометрическим вектором) называется ориентированный отрезок. При этом начало и конец ориентированного отрезка называются соответственно началом и концом вектора. Длина ориентированного отрезка называется длиной вектора.
Вектор обозначается 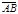 , где А – начало, а В – конец вектора. Если начало и конец вектора нас не интересуют, то вектор обозначают
, где А – начало, а В – конец вектора. Если начало и конец вектора нас не интересуют, то вектор обозначают 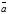 . Длина вектора обозначается
. Длина вектора обозначается 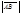 или
или 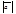 . Если начало и конец вектора совпадают, то вектор называют нулевым и обозначают
. Если начало и конец вектора совпадают, то вектор называют нулевым и обозначают 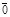 . Если начало и конец вектора – различные точки (А ¹ В), то существует и только один луч с началом А, проходящий через точку В. Этот луч задаёт в пространстве направление, которое называется направлением данного вектора. Нулевой вектор не имеет направления.
. Если начало и конец вектора – различные точки (А ¹ В), то существует и только один луч с началом А, проходящий через точку В. Этот луч задаёт в пространстве направление, которое называется направлением данного вектора. Нулевой вектор не имеет направления.
Определение 3. Два вектора называются равными, если они либо оба нулевые, либо имеют одинаковые длину и направление.
Равенство векторов обладает следующими очевидными свойствами:
1) рефлексивность (всякий вектор равен сам себе);
2) симметричность (если 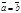 , то
, то 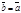 );
);
3) транзитивность (если 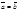 и
и 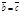 , то
, то 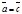 ).
).
Множество всех равных векторов можно задать 1) одним из векторов (ориентированным отрезком); 2) упорядоченной парой точек; 3) длиной и направлением (в случае ненулевого вектора). Пусть даны вектор 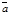 и точка А. Если
и точка А. Если 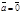 , то существует и только один вектор с началом в точке А, равный данному вектору. Это вектор
, то существует и только один вектор с началом в точке А, равный данному вектору. Это вектор 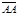 (т.е. В = А). Если
(т.е. В = А). Если 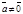 , то существует и только один луч, сонаправленный с вектором
, то существует и только один луч, сонаправленный с вектором 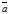 . На этом луче существует и только одна точка В, расстояние от которой до точки А равно
. На этом луче существует и только одна точка В, расстояние от которой до точки А равно 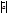 . Но тогда
. Но тогда 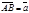 . Будем говорить, что вектор
. Будем говорить, что вектор 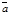 отложен от точки А. Итак, любой вектор можно отложить от любой точки и только единственным образом.
отложен от точки А. Итак, любой вектор можно отложить от любой точки и только единственным образом.
2. Сложение векторов: определение, свойства.
Пусть 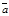 и
и 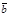 - любые два вектора. Чтобы к вектору
- любые два вектора. Чтобы к вектору 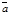 прибавить вектор
прибавить вектор 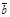 нужно отложить вектор
нужно отложить вектор 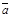 от любой точки А (
от любой точки А (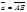 ), от конца В полученного вектора отложить вектор
), от конца В полученного вектора отложить вектор 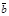 (
(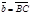 ). Тогда вектор
). Тогда вектор 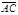 будет вектором суммы, т.е.
будет вектором суммы, т.е. 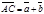 . Иными словами,
. Иными словами, 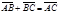 .
.
Свойства сложения векторов:
10. Для любых двух векторов их сумма определена и однозначна. (Следует из определения).
20. 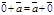 =
= 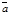 для любого вектора
для любого вектора  .
.
30. Для любого вектора 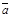 существует противоположный вектор (-
существует противоположный вектор (- 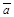 ) такой, что
) такой, что 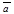 + (-
+ (- 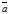 ) =
) = 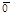 .
.
40. 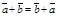 для любых векторов
для любых векторов 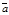 и
и 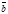 .
.
Доказательство. В случае, когда хотя бы один из векторов нулевой, утверждение следует из предыдущего свойства. Остаётся рассмотреть ненулевые векторы. При этом возможны следующие случаи.
а) Векторы 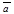 и
и 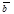 не параллельны. Пусть
не параллельны. Пусть 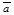 +
+ 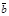 =
= 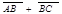 .
.
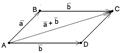
Отложим от точки А вектор 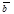 , пусть
, пусть 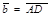 . Так как
. Так как 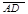 и
и 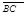 имеют одинаковые длины и направления, то АВСD – параллелограмм. Следовательно, отрезки АВ и DC тоже имеют одинаковые длины и направления. Следовательно,
имеют одинаковые длины и направления, то АВСD – параллелограмм. Следовательно, отрезки АВ и DC тоже имеют одинаковые длины и направления. Следовательно, 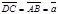 . По правилу сложения векторов
. По правилу сложения векторов 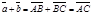 и
и 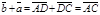 . Отсюда
. Отсюда 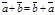 .
.


б) Векторы 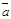 и
и 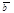 параллельны и одинаково направлены (сонаправлены). В этом случае при откладывании от точки А получим
параллельны и одинаково направлены (сонаправлены). В этом случае при откладывании от точки А получим 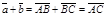 ,
, 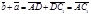 Векторы
Векторы 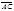 и
и 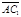 сонаправлены с вектором
сонаправлены с вектором 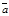 , поэтому сонаправлены между собой. Очевидно,
, поэтому сонаправлены между собой. Очевидно, 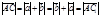 . Следовательно,
. Следовательно, 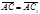 , т.е.
, т.е. 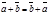 .
.
Определение 4. Векторы называются коллинеарными, если их можно отложить на одной прямой.
Очевидно, два вектора неколлинеарны óони ненулевые и не параллельные. Из случая а) проведённого доказательства следует ещё одно правило сложения неколлинеарных векторов: Чтобы сложить два неколлинеарных вектора, достаточно отложить их от одной точки, построить на них, как на сторонах, параллелограмм, тогда диагональ этого параллелограмма, идущая из данной точки, будет задавать вектор суммы.
50. 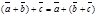 для любых векторов
для любых векторов 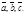 Доказательство. Для левой части получим
Доказательство. Для левой части получим 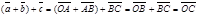 . Для правой части
. Для правой части 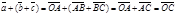 . Результаты равны.
. Результаты равны.
Определение 5.Разностью упорядоченной пары векторов называется сумма первого вектора и вектора, противоположного второму, т.е. 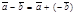 . чтобы вычесть из одного вектора второй, достаточно отложить оба вектора от одной точки. Тогда вектор, соединяющий концы полученных отрезков и направленный в сторону уменьшаемого, будет вектором разности. Очевидно, это правило не зависит от того, будут ли векторы коллинеарными или неколлинеарными.
. чтобы вычесть из одного вектора второй, достаточно отложить оба вектора от одной точки. Тогда вектор, соединяющий концы полученных отрезков и направленный в сторону уменьшаемого, будет вектором разности. Очевидно, это правило не зависит от того, будут ли векторы коллинеарными или неколлинеарными.
Свойства разности
10. Для любой упорядоченной пары векторов их разность определена и однозначна.
20. Разность двух векторов антикоммутативна. 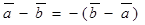 для любых векторов
для любых векторов 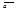 и
и 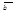 .
.
30. Не выполняется ассоциативный закон, а именно 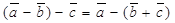 для любых векторов
для любых векторов 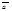 ,
, 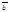 и
и 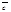
40. Выполняются дистрибутивные законы: 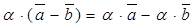 и
и 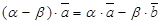 для любых векторов
для любых векторов 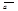 ,
, 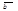 и любых действительных чисел a, b.
и любых действительных чисел a, b.
3. Умножение вектора на действительное число: определение, свойства.
Произведением ненулевого вектора 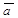 на отличное от нуля действительное число a называется такой вектор
на отличное от нуля действительное число a называется такой вектор 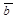 (обозначение
(обозначение 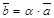 ), что
), что 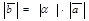 ,
, 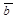
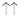
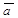 , если a > 0,
, если a > 0,
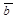
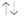
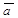 , если a < 0.
, если a < 0.
Если 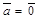 или a = 0, то вектор
или a = 0, то вектор 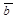 считается равным нулевому вектору.
считается равным нулевому вектору.
Свойства операции умножения вектора на действительное число.
10. Произведение любого вектора на любое действительное число определено и однозначно.
20. 1 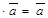 для любого вектора
для любого вектора 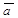 .
.
30. 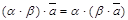 для любого вектора
для любого вектора 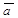 и любых действительных чисел a, b.
и любых действительных чисел a, b.
Доказательство. Возможны случаи.
1) a = 0, или b = 0, или 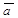 =
= 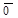 . В этом случае равенство очевидно.
. В этом случае равенство очевидно.
2) a ¹ 0, b ¹ 0 и 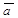 ¹
¹ 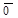 . Сравним длины и направления векторов, стоящих в левой и правой частях доказываемого равенства.
. Сравним длины и направления векторов, стоящих в левой и правой частях доказываемого равенства.
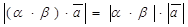 ,
, 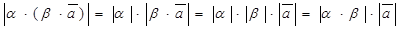 .
.
Следовательно, 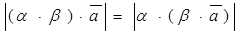 . Так как направления векторов зависят от знаков коэффициентов, то рассмотрим все возможные случаи.
. Так как направления векторов зависят от знаков коэффициентов, то рассмотрим все возможные случаи.
а) a и b одного знака (пусть a > 0, b > 0). В этом случае a × b > 0.
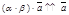 ,
, 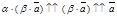 , следовательно,
, следовательно, 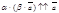 .
.
Итак, левая и правая части доказываемого равенства имеют одинаковые длины и направления, поэтому они равны.
б) a и b имеют разные знаки (пусть a > 0, b < 0). В этом случае a × b < 0.
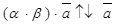 .
. 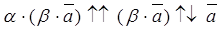 .
.
Снова получили, что левая и правая части доказываемого равенства имеют одинаковые длины и направления, поэтому они равны.
40. 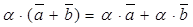 и (
и (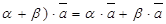 для любых векторов
для любых векторов 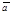 ,
, 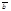 и любых действительных чисел a, b.
и любых действительных чисел a, b.
4. Коллинеарные векторы: определение, свойства, необходимые и достаточные условия коллинеарности двух векторов (три условия). Базис в пространстве коллинеарных векторов.
Определение 4. Векторы называются коллинеарными, если их можно отложить на одной прямой.
Свойства коллинеарных векторов.
10. Нулевой вектор коллинеарен с любым вектором.
20. Противоположные векторы коллинеарны.
30. При сложении двух коллинеарных векторов получается вектор, коллинеарный с данными векторами. Следовательно, множество коллинеарных векторов замкнуто относительно операции сложения.
40. Если вектор умножить на действительное число, то получится вектор, коллинеарный данному. Следовательно, множество коллинеарных векторов замкнуто относительно операции умножения на действительное число.
50. Если два вектора коллинеарны, то хотя бы один из них можно представить в виде произведения другого на действительное число.
Доказательство. Пусть векторы  и
и 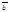 коллинеарны. Если вектор
коллинеарны. Если вектор 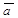 =
= 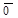 , то
, то 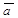 = 0
= 0 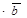 . Если
. Если 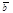 =
= 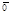 , то
, то 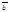 = 0 ×
= 0 × 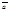 . Если
. Если 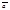 ¹
¹ 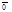 ,
, 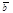 ¹
¹ 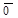 и
и 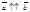 , то
, то 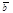 =
= 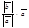 . Если
. Если 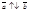 , то
, то 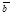 = -
= - 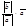 .
.
Из двух последних свойств, следуют следующие два свойства:
60. (Необходимое и достаточное условие коллинеарности двух векторов)
Два вектора коллинеарны ó хотя бы один из них можно представить в виде произведения другого на действительное число. Для коллинеарности двух ненулевых векторов 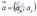 и
и  на плоскости необходимо и достаточно, чтобы их координаты были связаны соотношениями:
на плоскости необходимо и достаточно, чтобы их координаты были связаны соотношениями:  или
или  . Для коллинеарности двух ненулевых векторов
. Для коллинеарности двух ненулевых векторов 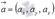 и
и 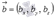 в пространстве необходимо и достаточно, чтобы
в пространстве необходимо и достаточно, чтобы  или
или  .
.
70. Если вектор 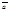 не нулевой, то любой вектор, коллинеарный с вектором
не нулевой, то любой вектор, коллинеарный с вектором 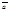 , можно представить в виде
, можно представить в виде 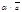 . Иными словами, для задания множества всех коллинеарных векторов достаточно задать один ненулевой из них.
. Иными словами, для задания множества всех коллинеарных векторов достаточно задать один ненулевой из них.
Наконец, из всех приведённых свойств можно сделать вывод, что относительно сложения векторов и умножения вектора на действительное число множество коллинеарных векторов ведёт себя так же как множество всех геометрических векторов.
5.Компланарные векторы: определение, свойства, необходимые и достаточные условия компланарности трёх векторов (четыре условия). Базис в пространстве компланарных векторов.
Опр. Векторы называются компланарными, если их можно отложить в одной плоскости.
Свойства компланарных векторов.
10. Коллинеарные векторы компланарны. Иными словами, во множество всех возможных компланарных между собой векторов вместе с каждым его вектором входят все векторы, коллинеарные с ним. В частности, нулевой вектор содержится в любом таком множестве и вместе с каждым вектором в это множество входит противоположный ему вектор. Отсюда же следует, что множество компланарных векторов замкнуто относительно операции умножения на действительное число.
20. Сумма двух векторов есть вектор, компланарный с ними. Следовательно, множество компланарных векторов замкнуто относительно операции сложения.
30. Три вектора компланарны тогда и только тогда, когда хотя бы один из них можно представить в виде линейной комбинации двух других.
Доказательство. Þ Пусть векторы 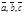 компланарны. Возможны два случая.
компланарны. Возможны два случая.
1) Среди данных векторов есть хотя бы одна пара коллинеарных векторов. Пусть 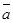 и
и 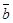 коллинеарны. Тогда, по свойствам коллинеарных векторов, хотя бы один из них можно выразить через другой. Пусть
коллинеарны. Тогда, по свойствам коллинеарных векторов, хотя бы один из них можно выразить через другой. Пусть 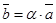 . Тогда
. Тогда 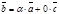 , т.е. вектор
, т.е. вектор 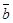 есть линейная комбинация векторов
есть линейная комбинация векторов 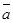 и
и 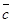 .
.
2) Данные векторы попарно не коллинеарны. Отложим их от одной точки О. Пусть 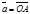 , , 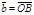 , , 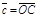 . Отрезки ОА, ОВ, ОС попарно не параллельны. Проведём СD ïïОА так, что D Î ОВ (прямой ОВ). Тогда . Отрезки ОА, ОВ, ОС попарно не параллельны. Проведём СD ïïОА так, что D Î ОВ (прямой ОВ). Тогда 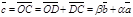 , т.е. вектор , т.е. вектор 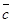 есть линейная комбинация векторов есть линейная комбинация векторов 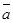 и и 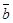 . .
| 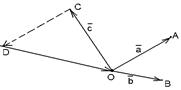 Рис. 9
Рис. 9
|
Ü Пусть 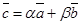 . По свойствам 10 и 20 следует, что вектор
. По свойствам 10 и 20 следует, что вектор 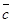 компланарен с векторами
компланарен с векторами 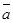 и
и 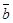 .
.
40. Если векторы 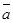 и
и 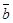 не коллинеарны, то любой компланарный с ними вектор можно представить в виде их линейной комбинации.
не коллинеарны, то любой компланарный с ними вектор можно представить в виде их линейной комбинации.
50. Из свойств 10 и 20 следует, что множество всех возможных компланарных векторов относительно операций сложения векторов и умножения вектора на действительное число ведёт себя так же, как множество всех коллинеарных векторов и как множество всех геометрических векторов. Кроме того, для задания множества всех возможных компланарных векторов достаточно задать любые два не коллинеарные из них.
Необходимые и достаточные условия компланарности трёх векторов:
Для компланарности трех векторов 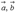 и
и 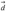 трехмерного пространства необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.
трехмерного пространства необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.
3 вектора комплонарны óхотябы один из них можно представить ка сумму двух других с использованием коэфицентов.
6. Теорема о разложении вектора по трём некомпланарным векторам.
Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом.
Док-во: Отложим векторы 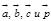 от одной точки. через точку P,проведем
от одной точки. через точку P,проведем 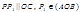 тогда по правилу треугольника
тогда по правилу треугольника 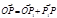 .
. 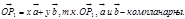
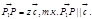
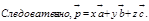
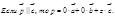
7. Векторное пространство: определение, примеры, базис.
Опр. Множество векторов V называется векторным пространством, если в нём определены две алгебраические операции: сложение векторов и умножение вектора на действительное число, удовлетворяющие следующим требованиям:
1. Множество V замкнуто относительно обеих операций.
2. 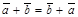 для любых векторов
для любых векторов 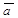 и
и 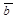 (коммутативный закон сложения).
(коммутативный закон сложения).
3. 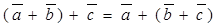 для любых векторов
для любых векторов 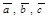 (ассоциативный закон сложения).
(ассоциативный закон сложения).
4. Существует 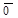 , такой, что
, такой, что 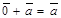 для любого вектора
для любого вектора 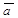 .
.
5. Для любого вектора 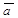 существует противоположный вектор (
существует противоположный вектор ( 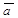 ) такой, что
) такой, что 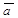 + (
+ ( 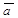 ) =
) = 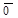 .
.
6. 1 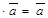 для любого вектора
для любого вектора 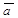 .
.
7. 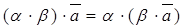 для любого вектора
для любого вектора 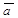 и любых действительных чисел a, b..
и любых действительных чисел a, b..
8. 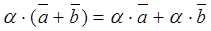 и (
и (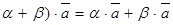 для любых векторов
для любых векторов 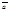 ,
, 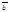 и любых действительных a, b. (дистрибутивные законы сложения относительно умножения на действительное число).
и любых действительных a, b. (дистрибутивные законы сложения относительно умножения на действительное число).
Примеры векторных пространств (следуют из предыдущего материала).
1. Множество всех геометрических векторов.
2. Множество всех компланарных векторов.
3. Множество всех коллинеарных векторов.
4. Множество, состоящее из одного нулевого вектора.
Опр9. Система векторов 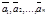 (1) данного векторного пространства называется линейно независимой, если линейная комбинация этих векторов равна нулевому вектору только с нулевыми коэффициентами.
(1) данного векторного пространства называется линейно независимой, если линейная комбинация этих векторов равна нулевому вектору только с нулевыми коэффициентами.
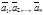 - линейно независима Û (
- линейно независима Û (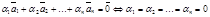 ).
).
Система векторов 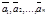 (1) называется линейно зависимой, если существует ненулевой набор коэффициентов a1, a2, …, an, такой, что
(1) называется линейно зависимой, если существует ненулевой набор коэффициентов a1, a2, …, an, такой, что 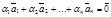 .
.
Опр10. Система векторов (1) называется максимальной линейно независимой, если сама она линейно независима, но при добавлении к ней любого другого вектора из данного векторного пространства она становится линейно зависимой.
Теорема 1. Линейно независимая система векторов 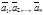 (1) данного векторного пространства V является максимальной линейно независимой ó любой вектор из V можно представить в виде линейной комбинации векторов системы (1).
(1) данного векторного пространства V является максимальной линейно независимой ó любой вектор из V можно представить в виде линейной комбинации векторов системы (1).
Доказательство. Þ Пусть системе векторов 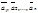 является максимальной линейно независимой и пусть
является максимальной линейно независимой и пусть 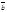 - любой вектор из V. По определению 10, система
- любой вектор из V. По определению 10, система 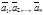 ,
, 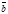 будет линейно зависимой, т.е. найдётся такой ненулевой набор коэффициентов a1, a2, …,an, b, что
будет линейно зависимой, т.е. найдётся такой ненулевой набор коэффициентов a1, a2, …,an, b, что 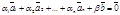 . Если бы b = 0, то
. Если бы b = 0, то 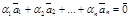 с ненулевым набором коэффициентов, что противоречит определению (10). Следовательно, b ¹ 0 и, поэтому
с ненулевым набором коэффициентов, что противоречит определению (10). Следовательно, b ¹ 0 и, поэтому 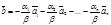 . Итак, любой вектор
. Итак, любой вектор 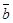 является линейной комбинацией векторов системы (1).
является линейной комбинацией векторов системы (1).
Ü Пусть любой вектор 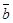 можно представить в виде
можно представить в виде 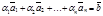 . Отсюда следует, что
. Отсюда следует, что 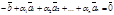 . Так как набор коэффициентов (-1, a1, a2, …,an) ненулевой, то система векторов
. Так как набор коэффициентов (-1, a1, a2, …,an) ненулевой, то система векторов 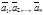 ,
, 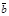 будет линейно зависимой. Следовательно, система (1) будет максимальной линейно независимой.
будет линейно зависимой. Следовательно, система (1) будет максимальной линейно независимой.
Примеры.
1. Во множестве всех геометрических векторов любая тройка некомпланарных векторов является максимальной линейно независимой системой векторов.
2. Во множестве всех компланарных векторов любая пара неколлинеарных векторов является максимальной линейно независимой системой векторов.
3. Во множестве всех коллинеарных векторов любая максимальная линейно независимая система состоит из одного ненулевого вектора.
4. Векторное пространство, состоящее из одного нулевого вектора, не имеет линейно независимых систем векторов.
8.Координаты вектора в данном базисе: определение, примеры, свойства. Действия с векторами в координатах.
Определение 11. Базисом векторного пространства называется любая упорядоченная максимальная линейно независимая система его векторов.
(Обратите внимание: если система векторов 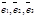 является максимальной линейно независимой, то системы
является максимальной линейно независимой, то системы 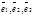 ;
; 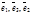 ;
; 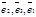 являются различными базисами.)
являются различными базисами.)
Примеры.
1. Во множестве всех геометрических векторов базисом является любая упорядоченная тройка некомпланарных векторов.
2. Во множестве всех компланарных векторов базисом является любая упорядоченная пара неколлинеарных векторов.
3. Во множестве всех коллинеарных векторов базисом является любой ненулевой вектор.
4. Векторное пространство, состоящее из одного нулевого вектора, не имеет базиса.
Определение 12. Число векторов в базисе векторного пространства называется размерностью этого пространства.
Следовательно, множество всех геометрических векторов есть трёхмерное векторное пространство. Множество всех компланарных векторов – двумерное векторное пространство. Множество всех коллинеарных векторов – одномерное векторное пространство.
Определение 13. Координатами вектора в данном базисе называется упорядоченный набор коэффициентов, с помощью которых этот вектор выражается через базисные векторы.
Пусть е = 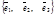 - базис и
- базис и 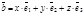 . Упорядоченный набор {х, у, z} - это координаты вектора
. Упорядоченный набор {х, у, z} - это координаты вектора 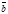 в базисе е. Обозначение
в базисе е. Обозначение 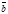 = {х, у, z}. Если используется несколько базисов, то обозначают
= {х, у, z}. Если используется несколько базисов, то обозначают 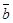 = {х, у, z} е.
= {х, у, z} е.
Свойства координат (все свойства будем доказывать для трёхмерного векторного пространства).
10. В данном базисе каждый вектор имеет единственный набор координат.
Доказательство. Пусть е = 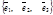 - базис векторного пространства и
- базис векторного пространства и 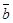 - любой вектор этого пространства. Предположим, что
- любой вектор этого пространства. Предположим, что 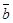 имеет два набора координат, т.е.
имеет два набора координат, т.е. 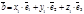 и
и 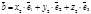 . Тогда
. Тогда 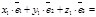
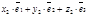 . Отсюда
. Отсюда 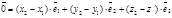 . Так как векторы
. Так как векторы 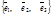 линейно независимы, то последнее равенство возможно только при нулевых коэффициентах. Следовательно, х1 = х2, у1 = у2, z1 = z2.
линейно независимы, то последнее равенство возможно только при нулевых коэффициентах. Следовательно, х1 = х2, у1 = у2, z1 = z2.
20. Если векторы заданы координатами в одном и том же базисе, то
а) при сложении (вычитании) векторов их соответствующие координаты складываются (вычитаются);
б) при умножении вектора на действительное число на это число умножается каждая его координата.
Доказательство.
Пусть е = 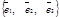 - базис векторного пространства,
- базис векторного пространства, 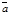 = {х1 , у1, z1}и
= {х1 , у1, z1}и 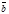 = {х2, у2, z2}. Тогда
= {х2, у2, z2}. Тогда 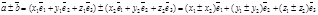 . Отсюда
. Отсюда 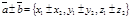 . Так как
. Так как 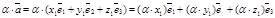 , то
, то 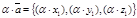 .
.
30. Два вектора коллинеарны тогда и только тогда, когда их координаты в одном и том же базисе пропорциональны.
40. Три вектора компланарны тогда и только тогда, когда определитель, строчками которого являются координаты данных векторов, равен нулю.
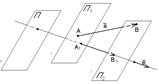
9. Проекция на прямую параллельно данной плоскости: определение, свойства. Векторная проекция вектора, её свойства.
Пусть l – прямая, П – плоскость и l 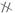 П. Пусть М – произвольная точка. Через точку М проведём плоскость П1, параллельную П. Пусть М1 = l Ç П1. Точка М1 называется проекцией точки М на прямую l параллельно плоскости П.
П. Пусть М – произвольная точка. Через точку М проведём плоскость П1, параллельную П. Пусть М1 = l Ç П1. Точка М1 называется проекцией точки М на прямую l параллельно плоскости П.
Свойства проекций.
10. Каждая точка имеет проекцию и только одну.
20. Точка совпадает со своей проекцией тогда и только тогда, когда она лежит на прямой l.
30. Точки имеют одну и ту же проекцию тогда и только тогда, когда они лежат в одной плоскости, параллельной П.
40. Если отрезок параллелен плоскости П, то он проектируется в точку. Если отрезок не параллелен плоскости П, то его проекция – отрезок.
50. Проекция ориентированного отрезка есть ориентированный отрезок. Следовательно, проекцией вектора будет вектор. Он называется векторной проекцией данного вектора и обозначается 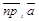 (параллельно П). Если проектирование идёт параллельно только одной плоскости, то слова в скобках можно опускать.
(параллельно П). Если проектирование идёт параллельно только одной плоскости, то слова в скобках можно опускать.
60. Равные и параллельные отрезки имеют равные проекции.
Доказательство. Пусть отрезки [АВ] и [СD] равны и параллельны. Если [АВ] параллелен плоскости П, то [СD] тоже параллелен плоскости П. В этом случае оба отрезка проектируются в точку. Следовательно, их проекции равны. Пусть [АВ], а поэтому и [СD], не параллельны плоскости П. Пусть [АВ] проектируется в [А1В1], а [СD] - в [С1D1]. При параллельном переносе на вектор 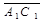 Плоскость П1 перейдёт в П3, П2 - в П4, прямая l - сама в себя. Следовательно, все отрезки с концами в плоскостях П1 и П2 перейдут в некоторые отрезки с концами в плоскостях П3 и П4. Отсюда и следует, что [А1В1] равен и параллелен [С1D1].
Плоскость П1 перейдёт в П3, П2 - в П4, прямая l - сама в себя. Следовательно, все отрезки с концами в плоскостях П1 и П2 перейдут в некоторые отрезки с концами в плоскостях П3 и П4. Отсюда и следует, что [А1В1] равен и параллелен [С1D1].
70. Если 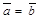 , то
, то 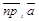 =
= 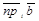 .
.
Доказательство. Так как равные векторы имеют равные векторные проекции, то при сложении первый вектор можно отложить от любой точки. Пусть О Î l, 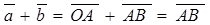 . Если А ® А1, В ® В1, то
. Если А ® А1, В ® В1, то 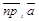 =
= 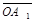 ,
, 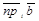 =
= 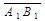 ,
, 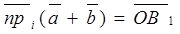 . Так как
. Так как 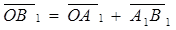 , то
, то 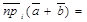
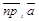 +
+ 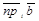 .
.
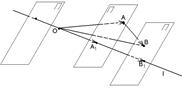
80. 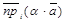 = a ×
= a × 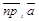 .
.
10. Числовая проекция вектора на ось, её свойства.
Определение 14. Осью называется прямая с фиксированным на ней единичным вектором. Этот вектор называется ортом оси.
Пусть 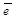 - орт оси,
- орт оси, 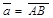 - произвольный вектор,
- произвольный вектор, 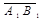 =
= 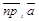 . Так как векторы
. Так как векторы 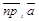 и
и 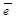 коллинеарны и
коллинеарны и 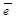
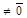 , то
, то 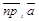 =
= 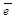 . Число называется числовой проекцией вектора
. Число называется числовой проекцией вектора 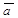 на данную ось и обозначается прl
на данную ось и обозначается прl 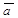 .
.
Из 70 и 80 свойств векторных проекций следует 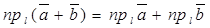 и
и 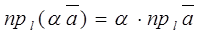
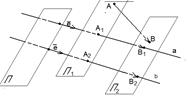
90. Векторные и числовые проекции вектора на сонаправленные оси параллельно одной и той же плоскости равны. Доказательство. Сонаправленные оси имеют один и тот же орт. Если 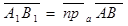 и
и 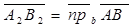 , то
, то 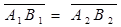 (по свойству отрезков параллельных прямых, заключённых между параллельными плоскостями). Итак, векторные проекции вектора на сонаправленные оси равны. Так как у этих осей один и тот же орт, то числовые проекции тоже равны.
(по свойству отрезков параллельных прямых, заключённых между параллельными плоскостями). Итак, векторные проекции вектора на сонаправленные оси равны. Так как у этих осей один и тот же орт, то числовые проекции тоже равны.
100. Так как направление оси можно задавать любым ненулевым вектором, сонаправленным с ортом оси, то можно говорить о проекции одного вектора на направление другого и обозначать 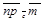 (проекция вектора
(проекция вектора 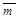 на направление вектора
на направление вектора 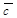 параллельно плоскости П).
параллельно плоскости П).
11. Ортогональная проекция вектора на ось, её свойства.
Определение 15. Проектирование называется ортогональным, Если плоскость П ортогональна оси.
При ортогональном проектировании достаточно из данной точки опустить на ось перпендикуляр.
Теорема 2. Числовая ортогональная проекция вектора на ось равна произведению длины этого вектора на косинус его угла с осью.
Доказательство. Пусть l – ось, 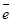 - её орт,
- её орт, 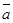 - произвольный вектор. Если
- произвольный вектор. Если 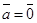 , то прl
, то прl 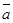 = 0, поэтому можно считать, что утверждение теоремы верно. Пусть
= 0, поэтому можно считать, что утверждение теоремы верно. Пусть 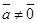 и a = (
и a = (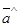 l).
l).
Возможны следующие случаи.
1) a = 0. В этом случае (рис. 17а) 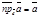 и пр
и пр 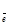 =
= 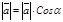 .
. 
2) 0 < a < 900. В этом случае (рис. 17б) 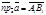 , пр
, пр 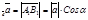 .
. 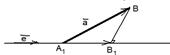
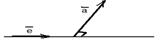 Рис. 17 в)
Рис. 17 в)
| 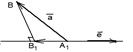 Рис. 17 г)
Рис. 17 г)
|
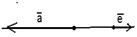 Рис. 17 д)
Рис. 17 д)
|
3) a = 900 (рис. 17в). В этом случае пр 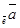 = 0 и, следовательно, пр
= 0 и, следовательно, пр 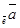 =
= 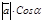 .
.
4) 900 < a < 1800 (рис. 17г). В этом случае 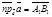 , пр
, пр 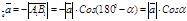 .
.
5) a = 1800 (рис. 17д). В этом случае пр 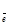 =
= 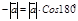 .
.
Итак, во всех случаях пр 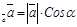 .
.
12. Скалярное произведение упорядоченной пары векторов: определение, свойства, формулы для вычисления. Применение скалярного произведения векторов к решению задач.
Определение 16. Скалярным произведением упорядоченной пары ненулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними. Если хотя бы один из перемножаемых векторов нулевой, то скалярное произведение считается равным нулю.
Обозначение: (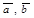 ), или
), или 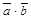 . Из определения
. Из определения 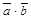 =
= 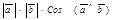 (1)
(1)
Свойства скалярного произведения.
10. Скалярное произведение любой упорядоченной пары векторов определено и однозначно.
20. 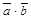 =
= 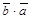 для любых векторов
для любых векторов 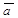 и
и 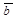 (коммутативный закон).
(коммутативный закон).
Доказательство. Если 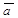 =
= 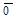 или
или 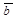 =
= 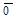 , то
, то 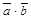 = 0 и
= 0 и 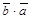 = 0, т.е. равенство верно.
= 0, т.е. равенство верно.
Пусть 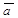 ¹
¹ 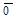 и
и 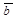 ¹
¹ 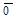 . Тогда
. Тогда 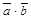 =
= 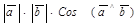 =
= 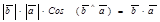 .
.
30. Если 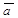 ¹
¹ 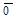 и
и 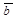 ¹
¹ 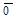 , то
, то 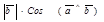 = пр
= пр 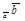 . Если
. Если 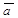 ¹
¹ 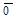 , а
, а 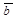 =
= 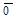 , то тоже
, то тоже 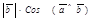 = пр
= пр 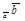 . Следовательно, при
. Следовательно, при 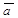 ¹
¹ 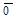 имеет место формула
имеет место формула 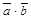 =
= 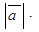 пр
пр 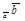 (2)
(2)
40. 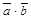 = 0 Û либо
= 0 Û либо 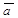 =
= 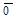 , либо
, либо 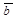 =
= 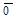 , либо
, либо 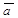 ^
^ 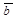 .
. 
50. (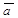 +
+ 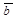 )×
)× 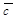 =
= 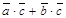 , для любых векторов
, для любых векторов 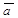 ,
, 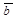 и
и 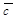 .
.
Доказательство. Если вектор 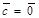 , то доказываемое равенство имеет вид 0 = 0 + 0, т.е. оно верно. Пусть
, то доказываемое равенство имеет вид 0 = 0 + 0, т.е. оно верно. Пусть 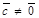 . Тогда (по формуле 2) (
. Тогда (по формуле 2) (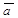 +
+ 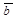 )×
)× 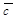 =
= 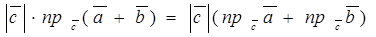 =
= 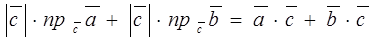 .
.
60. 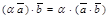 для любых векторов
для любых векторов 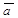 ,
, 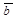 и любого действительного числа a.
и любого действительного числа a.
Доказательство. Если либо a = 0, либо хотя бы один из векторов 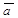 ,
, 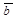 нулевой, то равенство очевидно. Пусть a ¹ 0 и векторы
нулевой, то равенство очевидно. Пусть a ¹ 0 и векторы 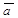 ,
, 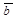 нулевые. Тогда
нулевые. Тогда
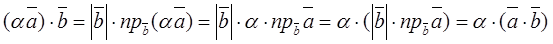 .
.
Произведение 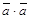 называется скалярным квадратом вектора
называется скалярным квадратом вектора 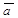 и обозначается
и обозначается
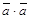 =
= 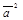 .
.
70. 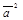 =
= 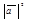 для любого вектора
для любого вектора 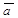 . Отсюда следует
. Отсюда следует 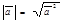 (3)
(3)
80. Если 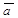 ¹
¹ 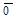 , то
, то 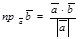 (4)
(4)
Формула (4) следует из (2).
90. Если 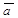 ¹
¹ 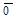 и
и 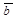 ¹
¹ 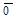 , то
, то 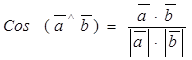 (5)
(5)
Замечание. Формулы 40, 70 – 100 определяют применение скалярного произведения для решения задач.
100. (Скалярное произведение в координатах)
Пусть В = 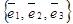 - базис,
- базис, 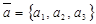 ,
, 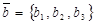 . Тогда
. Тогда
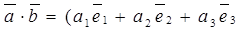 )
) 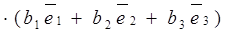 =
= 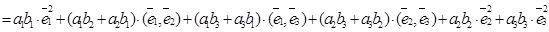 . (6)
. (6)
Если базис В = 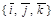 ортонормированный, то
ортонормированный, то 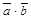 =
= 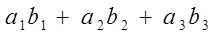 (7)
(7)
Из формулы (3) получаем, что в ортонормированном базисе 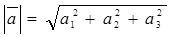
13.. Аффинная система координат на плоскости и в пространстве. Прямоугольная система координат.
На плоскости
Определение 17. Аффинным реперомназывается совокупность фиксированной точки и фиксированного базиса, т.е.
R = 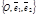 .
Точка О называется началом координат, векторы .
Точка О называется началом координат, векторы 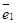 и и 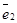 - координатными векторами.
Точка О вместе с каждым координатным вектором определяет ось. Эти оси называются координатными осями и обозначаются (Ох) и (Оу) (рис. 20). - координатными векторами.
Точка О вместе с каждым координатным вектором определяет ось. Эти оси называются координатными осями и обозначаются (Ох) и (Оу) (рис. 20).
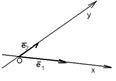 Рис. 20
Координатные оси разбивают плоскость на четыре угла. Их называют координатными углами. Координатные углы нумеруются в направлении кратчайшего поворота оси (Ох) к оси (Оу).
Говорят, что репер R =
Рис. 20
Координатные оси разбивают плоскость на четыре угла. Их называют координатными углами. Координатные углы нумеруются в направлении кратчайшего поворота оси (Ох) к оси (Оу).
Говорят, что репер R = 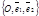 задаёт на плоскости систему аффинных координат.
Пусть М – произвольная точка плоскости.
Вектор задаёт на плоскости систему аффинных координат.
Пусть М – произвольная точка плоскости.
Вектор 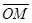 (рис. 21) называется радиусом- -вектором точки М (его часто обозначают одной буквой (рис. 21) называется радиусом- -вектором точки М (его часто обозначают одной буквой 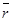 ). ).
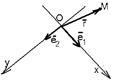 Рис. 21
Между множеством всех точек плоскости и множеством всех компланарных векторов, которые можно отложить в этой плоскости, устанавливается взаимнооднозначное соответствие. Следовательно, радиус-вектор точки вполне определяет эту точку и называется её векторной координатой. Обозначение М(
Рис. 21
Между множеством всех точек плоскости и множеством всех компланарных векторов, которые можно отложить в этой плоскости, устанавливается взаимнооднозначное соответствие. Следовательно, радиус-вектор точки вполне определяет эту точку и называется её векторной координатой. Обозначение М(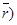 .
В базисе .
В базисе 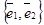 , входящем в данный репер, вектор , входящем в данный репер, вектор 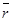 задаётся упорядоченной парой своих координат. Между множеством всех компланарных векторов и множеством всех упорядоченных пар действительных чисел тоже устанавливается взаимно однозначное соответствие. Итак,
М « задаётся упорядоченной парой своих координат. Между множеством всех компланарных векторов и множеством всех упорядоченных пар действительных чисел тоже устанавливается взаимно однозначное соответствие. Итак,
М «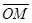 «{x, y}.
Отсюда следует, что между множеством всех точек плоскости и множеством всех упорядоченных пар действительных чисел устанавливается взаимнооднозначное соответствие. Следовательно, любая точка плоскости вполне определяется упорядоченной парой действительных чисел.
Определение 18. Аффинными координатами точкив репере R = «{x, y}.
Отсюда следует, что между множеством всех точек плоскости и множеством всех упорядоченных пар действительных чисел устанавливается взаимнооднозначное соответствие. Следовательно, любая точка плоскости вполне определяется упорядоченной парой действительных чисел.
Определение 18. Аффинными координатами точкив репере R = 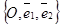 называются координаты её радиуса-вектора в базисе, входящем в этот репер.
М(х, у)R Û называются координаты её радиуса-вектора в базисе, входящем в этот репер.
М(х, у)R Û 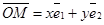 .
Замечание. Если зафиксирован только один репер, то координаты точки можно обозначать М(х, у). .
Замечание. Если зафиксирован только один репер, то координаты точки можно обозначать М(х, у).
| В пространстве
Определение 171. Аффинным реперомназывается совокупность фиксированной точки и фиксированного базиса, т.е.
R = 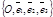 .
Точка О называется началом координат, векторы .
Точка О называется началом координат, векторы 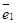 , , 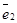 и и 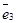 -координатными векторами.
Точка О вместе с каждым координатным вектором определяет ось. Эти оси называются координатными осями и обозначаются (Ох), (Оу) и (Оz) (рис. 201). -координатными векторами.
Точка О вместе с каждым координатным вектором определяет ось. Эти оси называются координатными осями и обозначаются (Ох), (Оу) и (Оz) (рис. 201).
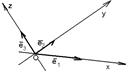 Рис. 201
Каждая пара координатных осей определяет плоскость. Их называют координатными плоскостями и обозначают (ХОУ), (ХОZ) и (УОZ). Координатные плоскости разбивают пространство на 8 трёхгранных углов. Их называют координатными углами.
Говорят, что репер R =
Рис. 201
Каждая пара координатных осей определяет плоскость. Их называют координатными плоскостями и обозначают (ХОУ), (ХОZ) и (УОZ). Координатные плоскости разбивают пространство на 8 трёхгранных углов. Их называют координатными углами.
Говорят, что репер R = 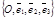 задаёт в пространстве систему аффинных координат.
Пусть М – произвольная точка пространства. Вектор задаёт в пространстве систему аффинных координат.
Пусть М – произвольная точка пространства. Вектор 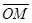 (рис.211) называется радиусом-вектором точки М (его часто обозначают одной буквой (рис.211) называется радиусом-вектором точки М (его часто обозначают одной буквой 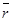 ). ).
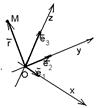 Рис.211
Между множеством всех точек плоскости и множеством всех геометрических векторов устанавливается взаимнооднозначное соответствие. Следовательно, радиус-вектор точки вполне определяет эту точку и называется её векторной координатой.
Обозначение М(
Рис.211
Между множеством всех точек плоскости и множеством всех геометрических векторов устанавливается взаимнооднозначное соответствие. Следовательно, радиус-вектор точки вполне определяет эту точку и называется её векторной координатой.
Обозначение М(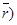 .
В базисе .
В базисе 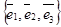 , входящем в данный репер, вектор , входящем в данный репер, вектор 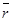 задаётся упорядоченной тройкой своих координат. Между множеством всех геометрических векторов и множеством всех упорядоченных троек действительных чисел тоже устанавливается взаимно однозначное соответствие. Итак,
М « задаётся упорядоченной тройкой своих координат. Между множеством всех геометрических векторов и множеством всех упорядоченных троек действительных чисел тоже устанавливается взаимно однозначное соответствие. Итак,
М «
 Сейчас читают про:
|
 2020-10-12
2020-10-12 208
208





