Предмет, основные понятия и основные разделы теоретической механики

Подготовка к экзамену

Теоретическая механика – это раздел механики, в котором излагаются основные законы механического движения и механического взаимодействия материальных тел.

Разделы -Статика - учение о силах и выводятся условия равновесия для твердых тел.

            -Кинематика - рассматривает движение тел как перемещение в пространстве; характеристики тел и причины, вызывающие движение, не рассматриваются. 

           - Динамика - изучает движение тел под действием сил.

  2. Предмет статики. Силы, системы сил. Аксиомы статики

Сила — это мера механического взаимодействия материальных тел между собой.

Система сил – это совокупность сил, действующих на механическую систему.

Плоская система сил – это система сил, линии действия которых лежат в одной плоскости.

Система сходящихся сил – это система сил, линии действия которых пересекаются в одной точке.

Произвольная система сил – это система сил, линии действия которых не пересекаются в одной точке.

Аксиомы статики  

Аксиома 1.Твердое тело под действием двух сил будет находиться в равновесии тогда и только тогда, когда эти силы равны по величине и направлены вдоль одной прямой в противоположные стороны

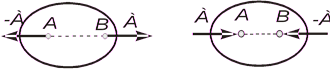
Аксиома 2.Действие любой системы сил на твердое тело не изменится, если к ней добавить или от нее отнять уравновешенную систему сил.

Аксиома 3.(Правило параллелограмма). Две силы, приложенные в одной точке, имеют равнодействующую, определяемую диагональю параллелограмма, построенного на этих силах и приложенную в этой же точке

Аксиома 4.Силы взаимодействия двух тел равны по величине и направлены вдоль одной прямой в противоположные стороны (третий закон Ньютона). Отметим, что в данном случае эти силы не уравновешивают друг друга так как приложены к разным телам

Аксиома 5.(Принцип освобождаемости от связей). Несвободное твердое тело можно рассматривать как свободное, если заменить все связи эквивалентными им по воздействию на тело силами, называемыми реакциями связей.

Аксиома 6.Равновесие деформируемого тела не нарушится, если тело считать абсолютно твердым (другими словами: равновесие тела не нарушается при наложении на него дополнительных связей)                                                     

         3. Система сходящихся сил (ССС). Проекции силы на оси координат. Условия равновесия ССС

Систе́ма сходя́щихся сил — это такая система сил, действующих на абсолютно твёрдое тело, в которой линии действия всех сил пересекаются в одной точке.

Проекция силы на ось- Величина проекции равна длине полученного отрезка. Если спроецированное направление совпадает с направлением оси x, то проекция положительная. Если спроецированное направление противоположно направлению оси x, то проекция отрицательная.

Определим проекцию силы F1 на ось y. Начало и конец вектора в нашем случае спроецируются на ось y в одну и ту же точку. «Длина» точки равна нулю. Поэтому F1y=0

Теперь более общий случай: сила F2 располагается под углом a к оси x

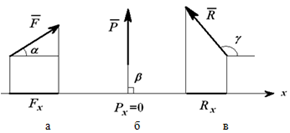Проекция силы на ось x равна силе, умноженной на косинус a

Проекция силы на ось у равна силе, умноженной на синус a

Условия равновесия сходящихся сил- Сходящиеся силы находятся в равновесии, если их равнодействующая равна нулю. 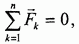 называемым векторным условием равновесия сходящихся сил

геометрическое условие равновесия сходящихся сил- чтобы сходящиеся силы находилисъ в равновесии, необходимо и достаточно, чтобы силовой многоугольник, построенный из этих сил, был замкнутым.

 для равновесия сходящихся сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на координатные оси были равны нулю.

        4. Пары сил. Теоремы о парах сил. Алгебраический и векторный момент пары сил.

Пара сил – система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело. Действие пары сил на твердое тело сводится к некоторому вращательному эффекту, который характеризуется величиной – момент пары.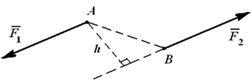

Теорема 1. Пара сил не имеет равнодействующей, т.е. пару сил нельзя заменить одной силой.

Теорема 2. Пара сил не является системой уравновешенных сил.

Следствие: пара сил, действующая на абсолютно твердое тело, старается вращать его.

Теорема 3. Сумма моментов сил пары относительно произвольного центра (точки) в пространстве является величиной неизменной и представляет собой вектор-момент этой пары.

Теорема 5 - об эквивалентности пар. Пары сил, моменты которых равны численно и по знаку, являются эквивалентными. Т.е. пару сил можно заменить или уравновесить только другой эквивалентной парой сил.

Теорема 6 - об уравновешенности пары сил. Пара сил составляет уравновешенную систему сил тогда и только тогда, когда момент пары равняется нулю.

Теорема 7 - о возможностях перемещения пары сил в плоскости ее действия. Пара сил, полученная перемещениям пары в любое место в плоскости ее действия, эквивалентна предоставленной паре.

Теорема 8 - о добавлении пар сил в плоскости. Момент пары, эквивалентной предоставленной системе пар в плоскости, равняется алгебраической сумме моментов составляющих пар. Т.е. для сложения пар сил необходимо сложить их моменты.

Алгебраический момент пары равен взятому с соответствующим знаком произведению модуля одной из сил пары на плечо пары M = ± F ∙ h.

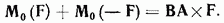 Таким образом, сумма моментов силы, составляющих пару, является вектором, не зависящим от положения точки, относительно которой вычисляется момент силы. Этот вектор называется векторным моментом пары

       5. Алгебраический и векторный момент силы относительно точки. Равенство векторного момента пары сил и векторного момента силы относительно точки

Алгебраическим моментом силы относительно точки называют произведение модуля силы на плечо силы относительно этой точки, взятое со знаком плюс или минус M0(F)=F*h

Векторным моментом силы относительно точки называют вектор приложенный в этой точке и равный по модулю, произведению силы на плечо силы относительно этой точки. Векторный момент направлен перпендикулярно плоскости, в которой лежат сила и точка, таким образом, что с его конца можно видеть "стремление" силы вращать тело против движения часовой стрелки.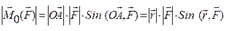

Mz(F)=Mo(F)*cosα Момент силы, относительно оси равен прекции вектора момента сил, относительно точки оси на эту ось.

         6. Параллельный перенос силы. Пример(доказательство)

Теорема - силу, приложенную к абсолютно твердому телу, можно, не изменяя оказываемого ею действия, переносить из данной точки в любую другую точку тела, прибавляя при этом пару с моментом, равным моменту переносимой силы относительно точки, куда сила переносится.

Пусть на твердое тело действует сила F, приложенная в точке А. Действие этой силы не изменяется, если в любой точке B тела приложить две уравновешенные силы F`и F`` такие, что F`=F, F``=-F. Полученная система трех сил и представляет собой силу F, равную F, но приложенную в точке В, и пару F, F с моментом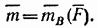

Пример.  На барабан 1 радиуса r намотаны в противоположных направлениях две нити, к концам которых прикладывают силы F и F`=-F; на барабан 2 того же радиуса намотана одна нить, к которой прикладывают силу, равную 2F. Рассмотрим, чем будут отличаться действия этих сил. На барабан 1 действует только пара сил F, F` с моментом, численно равным 2Fr вращающая барабан. Силу, действующую на барабан 2, можно заменить силой 2F`=2F приложенной к оси барабана, и парой 2F,2F`` В результате находим, что на этот барабан действуют: 1) пара с численно таким же, как и в первом случае, моментом 2Fr вращающая барабан, и 2) сила 2F` оказывающая давление на ось барабана.

Итак, оба барабана будут вращаться одинаково. Но при этом ось второго барабана испытывает давление, равное 2F, а ось первого барабана никакого давления не испытывает.

        7. Основная теорема статики (о приведении произвольной системы сил (ПСС) к данному центру). Условия равновесия ПСС в векторной форме. Частные случаи равновесия

Теорема о приведении системы сил: любая система сил, действующих на абсолютное твердое тело, при приведении к произвольному выбранному центру О, заменяется одной силой R, равной главному вектору системы сил и приложенной в центре приведения О, и одной парой с моментом М,равным главному моменту системы сил относительно О

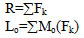,где  R- главный вектор системы сил

Lо- главный моментом системы сил(вместо Lo- писать Mo, а вместо Мо-mо)

Условия равновесия можно сформулировать так: для равновесия произвольной системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы суммы проекций всех сил на оси декартовой системы координат равнялись нулю и суммы моментов всех сил относительно этих осей также равнялись нулю. Т.е. чтобы выполнялось

Частные случаи. Условия равновесия пространственной системы параллельных сил.

Если силы, действующие на твердое тело, параллельны между собой, то можно выбрать такую систему координат, когда одна из ее осей, например Oz, параллельна направлению действия сил. Тогда из шести аналитических условий равновесия три выполняются тождественно, и система параллельных сил будет иметь только три условия равновесия:

 1-ая форма 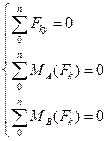2-ая форма 3-ья форма

              8. Момент силы относительно оси. Связь между моментом силы относительно точки и моментом силы относительно оси

1 определение

2 определение Таким образом, момент силы F относительно оси z равен алгебраическому моменту проекции этой силы на плоскость, перпендикулярную оси z, взятому относительно точки O пересечения оси с этой плоскостью Этот результат может служить другим определением понятия момента силы относительно оси.

Связь- Mz(F)=Mo(F)*cosαМомент силы, относительно оси равен прекции вектора момента сил, относительно точки оси на эту ось.

               9. Условия равновесия произвольной системы сил в координатной форме. Условия равновесия плоской системы сил

Первая форма условий равновесия Для равновесия произвольной плоской системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы главный вектор R этих сил и их главный момент M_o относительно произвольной точки O, лежащей в плоскости действия этих сил, были равны нулю, т.е. ΣF_kx = 0, ΣF_ky = 0, ΣM_o(F_k) = 0. 1.4

Вторая форма условий равновесия (теорема о трех моментах) алгебраическая сумма моментов сил относительно трех произвольных точек A,B,C, не лежащих на одной прямой, равна нулю, т.е.

ΣM_A(F_k) = 0, ΣM_B(F_k) = 0, ΣM_C(F_k) = 0 1.5 Из последнего равенства (1.4) следует, что сумма моментов всех сил относительно любой точки, следовательно, и точек А, В, С равняется нулю, т.е. выполняются условия (1.5).Достаточность условий (1.5) следует из того, что если выполняются условия (1.5), а данная система сил не находится в равновесии, то она должна была бы приводиться к равнодействующей, одновременно проходящей через точки А, В, С.

Это невозможно, т.к. точки А, В, С не лежат на одной прямой. Следовательно, если выполняются условия (1.5), то имеет место равновесие.

Третья форма условий равновесия – алгебраическая сумма моментов всех сил относительно двух любых точек A и B равна нулю и сумма проекций этих сил на ось Ox, не перпендикулярную к прямой, проходящей через точки A и B, равна нулю т.е.

ΣM_A(F_k) = 0, ΣM_B(F_k) = 0, ΣF_kx = 0. (1.6)

Необходимость этих условий, так же как и в предыдущем случае, следует из первой формы условий равновесия. Докажем их достаточность, т.е. докажем, что если выполняются условия (1.6), то рассматриваемая система находится в равновесии.

Выполнение первых двух условий (1.6) означает, что главный момент данной системы сил относительно центров приведения А и В равен нулю. Такая система может иметь равнодействующую, приложенную в центре приведения, и при R*¹0 линия действия равнодействующей проходит через точки А и В (рисунок 2.2).

 

Но по третьему условию из (1.6) проекция равнодействующей на ось Оx равна нулю. Так как ось Оx (рис.2) не перпендикулярна АВ, то это последнее условие может быть выполнено только в случае, если R*=0, т.е. когда рассматриваемая система сил уравновешена.

               10. Задача о равновесии ротора в плоском случае

Не нашел((((0((

               11. Примеры вычисления осевых моментов сил. Связи и реакции опор твердого тела в пространстве

Моменты силы относительно координатных осей можно получить, расписав векторное произведение

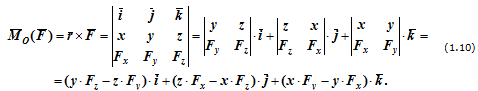
Шарнирно-неподвижная опора может изображаться по-разному. Она может быть заменена либо силой R с углом α (рисунок  в), либо двумя силами, например, X_A и Y_A (рисунок, г).

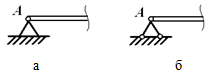
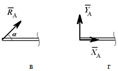
Всегда можно перейти от R и α к X_A и Y_A (и наоборот): X_A= Rcosα; Y_A= Rsinα;

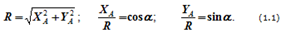
Шарнирно-подвижная опора (рисунок а) допускает (в данном случае) горизонтальное перемещение и не допускает вертикальное. Реакция направлена по нормали к опорной поверхности (рисунок 1.4, б).

Связи шарнирно-неподвижной опоры в точке A и шарнирно-подвижной опоры в точке B отброшены (рисунок 1.5, б), их действие заменено силами X_A, Y_A и R_B.

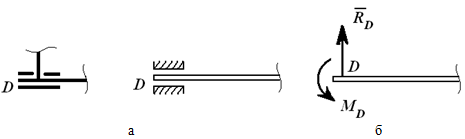
Скользящая заделк Отбросим втулку – получим действие на стержень силы R_D и M_D момента.

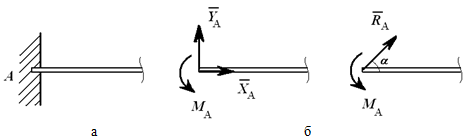
Консоль (глухая или жесткая заделка) не допускает никакого перемещения детали. Реакцией такой опоры являются неизвестная по величине и направлению сила R_A с углом α (или X_A и Y_A) и момент Μ_A (рисунок 1.8).

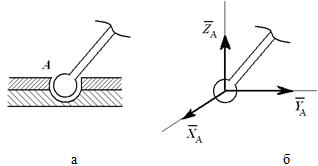
Шарнирно-неподвижная опора, или сферический шарнир (рисунока), заменена системой сил (рисунок б) X_A, Y_A и Z_A, т.е. силой, неизвестной по величине и направлению.

             12. Задача о равновесии ротора в пространстве и об определении статических реакций подшипников ротора

 

         13. Трение скольжения. Законы Кулона. Момент сил трения

Силой трения скольжения 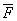(или просто силой трения) называется составляющая силы реакции связи, которая лежит в касательной плоскости к поверхностям соприкасающихся тел.

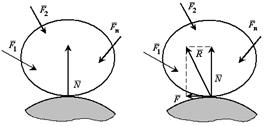
Величина предельной силы трения равна произведению статического коэффициента трения на нормальное давление или нормальную реакцию

коэффициент трения-f

Закон Кулона- Сухим трением называется трение, когда между поверхностями соприкасающихся тел нет смазывающего вещества.

1 закон) сила трения находится в общей касательной плоскости соприкасающихся поверхностей тел и направлена в сторону, противоположную направлению возможного скольжения тела под действием активных сил. 0≤F_mp≤F_mp^max;

2) максимальное значение силы трения при прочих равных условиях не зависит от площади контакта трущихся поверхностей и пропорционально нормальной реакции: F_mp^max=fN [Н],

Момент сил трения - Для трения скольжения 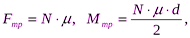(23.1)

где N - нормальное давление, Н; μ - коэффициент трения скольжения; d - диаметр цапфы вала и т.п., м.

Для трения качения 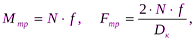(23.2)

где f - коэффициент трения качения, м; D_к - диаметр колеса, ролика и т.п., м

 

                  14. Центр системы параллельных сил

При повороте всех сил системы на один и тот же угол линия действия равнодействующей системы параллельных сил повернется в ту же сторону на тот же угол вокруг некоторой точки (рисунок, а).

Эта точка называется центром параллельных сил.

Согласно теореме Вариньона, если система сил имеет равнодействующую, то ее момент относительно любого центра (оси) равен сумме моментов всех сил системы относительно того же центра (оси).

 

Относительно оси x M_x(R) = ΣM_x(F_k), _-y_CR = Σy_kFk и y_C = Σy_kFk /Σ_Fk.

Относительно оси y M_y(R) = ΣM_y(F_k), _-x_CR = Σx_kFk и x_C = Σx_kFk /Σ_Fk.

Чтобы определить координату z_C, повернем все силы на 90° так, чтобы они стали параллельны оси y (рисунок б). Тогда M_z(R) = ΣM_z(F_k), _-z_CR = Σz_kFk и z_C = Σz_kFk /Σ_Fk.

     15. Координаты центра тяжести твердого тела

Исходя из полученных ранее общих формул, можно указать способы определения координат центров тяжести твердых тел:

1 Аналитический (путем интегрирования).

2 Метод симметрии. Если тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.

3 Экспериментальный (метод подвешивания тела).

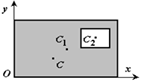
4 Разбиение. Тело разбивается на конечное число частей, для каждой из которых положение центра тяжести C и площадь S известны. Например, проекцию тела на плоскость xOy (рисунок 1.8) можно представить в виде двух плоских фигур с площадями S₁ и S₂ (S = S₁+ S₂). Центры тяжести этих фигур находятся в точках C₁(x₁, y₁) и C₂(x₂, y₂). Тогда координаты центра тяжести тела равны

5 Дополнение (метод отрицательных площадей или объемов). Частный случай способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Например, необходимо найти координаты центра тяжести плоской фигуры

 

координаты центра тяжести (интегральная формула