Для графов 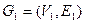 и
и 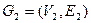 их объединение
их объединение 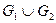 определяется как граф
определяется как граф 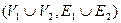 , а пересечение
, а пересечение  – как граф
– как граф 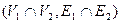 .
.
Дополнением (дополнительным графом) к графу 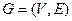 называется граф
называется граф  , у которого множество вершин то же, что у G, а множество ребер является дополнением множества E до множества всех неупорядоченных пар вершин. Иначе говоря, две различные вершины смежны в графе
, у которого множество вершин то же, что у G, а множество ребер является дополнением множества E до множества всех неупорядоченных пар вершин. Иначе говоря, две различные вершины смежны в графе  тогда и только тогда, когда они не смежны в графе G. Например,
тогда и только тогда, когда они не смежны в графе G. Например, 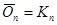 .
.
Под суммой  двух абстрактных графов понимают объединение графов с непересекающимися множествами вершин. Точнее говоря, имеется в виду следующее. Сначала вершинам графов-слагаемых присваиваются имена (пометки, номера) так, чтобы множества вершин не пересекались, затем полученные графы объединяются и пометки стираются (т.е. результат операции – тоже абстрактный граф). Операция сложения ассоциативна, то есть
двух абстрактных графов понимают объединение графов с непересекающимися множествами вершин. Точнее говоря, имеется в виду следующее. Сначала вершинам графов-слагаемых присваиваются имена (пометки, номера) так, чтобы множества вершин не пересекались, затем полученные графы объединяются и пометки стираются (т.е. результат операции – тоже абстрактный граф). Операция сложения ассоциативна, то есть  для любых трех графов. Поэтому можно образовывать сумму любого числа графов, не указывая порядка действий с помощью скобок. Если складываются k экземпляров одного и того же графа G, то полученный граф обозначается через
для любых трех графов. Поэтому можно образовывать сумму любого числа графов, не указывая порядка действий с помощью скобок. Если складываются k экземпляров одного и того же графа G, то полученный граф обозначается через 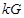 . Например,
. Например, 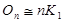 .
.
Соединением графов 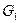 и
и 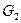 называется граф
называется граф 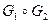 , получаемый из их суммы добавлением всех ребер, соединяющих вершины первого слагаемого с вершинами второго. Например,
, получаемый из их суммы добавлением всех ребер, соединяющих вершины первого слагаемого с вершинами второго. Например, 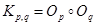 . На рисунке 1 слева изображен граф
. На рисунке 1 слева изображен граф 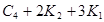 справа – граф
справа – граф 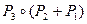 .
.

Рис. 1.
Произведение 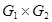 графов
графов 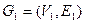 и
и 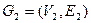 определяется следующим образом. Множеством вершин графа
определяется следующим образом. Множеством вершин графа 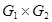 является декартово произведение множеств
является декартово произведение множеств 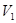 и
и 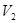 , то есть вершины этого графа – упорядоченные пары
, то есть вершины этого графа – упорядоченные пары 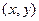 , где
, где 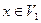 ,
, 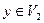 . Вершины
. Вершины  и
и  в графе
в графе 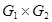 смежны тогда и только тогда, когда
смежны тогда и только тогда, когда 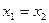 и
и 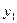 смежна с
смежна с 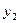 в графе
в графе 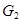 , или
, или 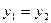 и
и 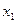 смежна с
смежна с 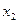 в графе
в графе 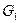 . С помощью операции произведения можно выразить некоторые важные графы через простейшие. Например, произведение двух путей дает прямоугольную решетку – см. рисунок 2.
. С помощью операции произведения можно выразить некоторые важные графы через простейшие. Например, произведение двух путей дает прямоугольную решетку – см. рисунок 2.
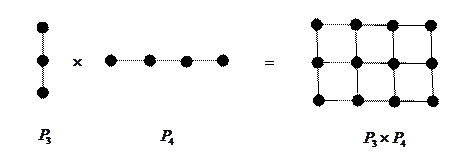
Рис. 2.
Другой пример – k- мерный куб 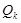 , определяемый следующим образом. Вершинами его являются всевозможные упорядоченные двоичные наборы длины k. Всего, таким образом, в этом графе
, определяемый следующим образом. Вершинами его являются всевозможные упорядоченные двоичные наборы длины k. Всего, таким образом, в этом графе 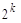 вершин. Вершины
вершин. Вершины 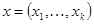 и
и 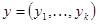 смежны в нем тогда и только тогда, когда наборы x и y различаются точно в одной координате. С помощью операции произведения граф
смежны в нем тогда и только тогда, когда наборы x и y различаются точно в одной координате. С помощью операции произведения граф 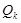 можно определить рекурсивно:
можно определить рекурсивно:
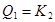 ,
, 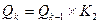 .
.
На рисунке 3 показано, как получается 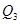 из
из 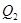 .
.
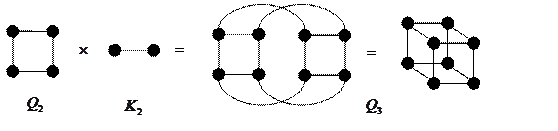
Рис. 3.
 2014-02-04
2014-02-04 761
761








