Некоторые различия между рассматриваемыми правилами решения могут возникнуть, если разным значениям 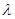 соответствуют различные совокупности параметров
соответствуют различные совокупности параметров  . Практически такая ситуация может возникнуть только в том случае, когда множество значений
. Практически такая ситуация может возникнуть только в том случае, когда множество значений 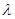 дискретно, то есть состоит из изолированных точек
дискретно, то есть состоит из изолированных точек 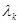 (
(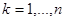 ). При этом апостериорный риск (6.5.8) может быть записан в виде
). При этом апостериорный риск (6.5.8) может быть записан в виде
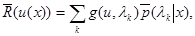 (6.5.18)
(6.5.18)
где 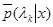 - оценочное значение апостериорной вероятности k -ro дискретного значения
- оценочное значение апостериорной вероятности k -ro дискретного значения 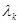 , которое определяется следующим выражением
, которое определяется следующим выражением
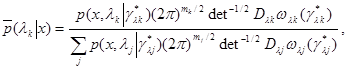 (6.5.19)
(6.5.19)
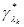 - оценка максимального правдоподобия параметров
- оценка максимального правдоподобия параметров  ; m k - число неизвестных параметров плотности вероятности
; m k - число неизвестных параметров плотности вероятности 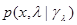 ;
; 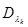 - значение матрицы
- значение матрицы 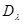 (6.5.6);
(6.5.6); 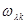 - значение функции
- значение функции 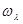 при
при 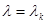 .
.
Для того чтобы правило решения, получающееся минимизацией (6.5.18), было вполне определенным, необходимо как-то задать величины 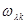 (
(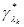 ). Если функция
). Если функция 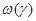 не задана, то, используя предполагавшееся ранее медленное изменение этой функции, можно оценить эти величины следующим образом:
не задана, то, используя предполагавшееся ранее медленное изменение этой функции, можно оценить эти величины следующим образом:
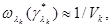 (6.5.20)
(6.5.20)
где 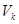 - эффективный объем области сосредоточения параметров
- эффективный объем области сосредоточения параметров  для
для 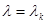 . В частности, если область
. В частности, если область 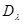 значений параметров
значений параметров  ограничена, то
ограничена, то 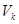 по порядку величины совпадает с объемом этой области для
по порядку величины совпадает с объемом этой области для 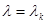 .
.
 2014-02-04
2014-02-04 227
227







