Линейные диаграммы. Линейные и круговые диаграммы (годографы)

Линейные и круговые диаграммы (годографы)

При исследовании электрических цепей часто бывает, что какая-либо комплексная величина определяется уравнением вида:

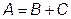; (7.27)

где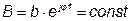

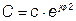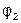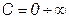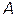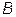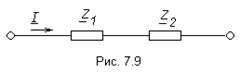
- изменяющаяся комплексная величина с неизменным аргументом и переменным модулем с (). Геометрически величина представляет собой сумму двух векторов в комплексной плоскости, один из которых постоянен - , а другого - 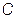неизменным остаётся направление, но изменяется длина. Для пояснения рассмотрим электрическую цепь, состоящую из двух последовательно соединённых приёмников (рис. 7.9).

Пусть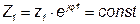

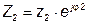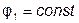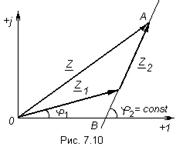
такое, что , а 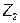- изменяется. Комплексное сопротивление всей цепи

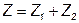
Изобразим его на комплексной плоскости (рис. 7.10).

Модуль сопротивления 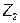изменяется по линии АВ при неизменном аргументе 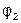. Прямую АВ называют линией переменного параметра.

7.7.2 Круговые диаграммы четырёхполюсников

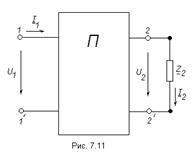
Рассмотрим схему с четырёхполюсником на рис. 7.11.

В четырёхполюснике зависимость между входным и выходным токами имеет линейный характер.

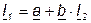, (7.28)

где 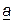и 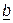- комплексные числа.

Определим эти коэффициенты.

Если ветвь разомкнута (нагрузка 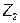отключена - режим холостого хода), то 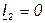и 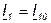. Подставив эти значения в уравнение 7.28, запишем: .

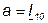Если же ветвь замкнута накоротко (режим короткого замыкания), то 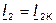и 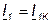. Поэтому

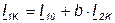. (7.29)

Отсюда выразим коэффициент :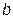

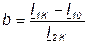. (7.30)

Подставив 7.30 и 7.29 в 7.28, получим:

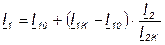. (7.31)

Если подать питание со стороны зажимов , то при коротком замыкании ветви 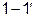получим ток:

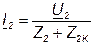, (7.32)

где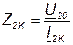

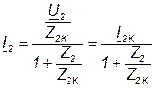
Откуда

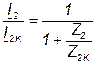. (7.33)

Подставив 7.33 в 7.31, запишем следующее:

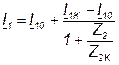, (7.34)

где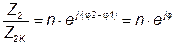

Для построения кривой диаграммы можно воспользоваться следующей последовательностью:

1. Откладываем вектор 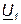в соответствующем масштабе 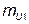. На диаграмме направляем вдоль оси +1 (примем направление оси +1 вверх).

2. Определяем ток 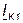при 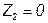, то есть при коротком замыкании на выводах приёмника.

3. Выбираем масштаб для тока 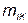и откладываем вектор 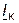(отрезок ОК на диаграмме) (примем для определённости ток 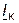отстающим от напряжения ).

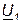4. На отрезке ОК откладываем сопротивление 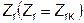в масштабе 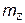(на диаграмме ).

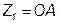5. Из точки А под углом -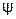(так принято) к вектору 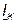проводим линию переменного параметра АВ (Л.П.П.). Для определённости предположим, что 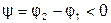, то есть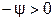

6. Из начала координат проводим прямую OD перпендикулярно АВ.

7. Находим центр С кривой диаграммы как точку пересечения прямой OD и перпендикуляра, восставленного в середине хорды ОК.

8. Циркулем проводим дугу диаграммы, ограниченную хордой ОК.

Пример круговой диаграммы предоставлен на рис. 7.12.

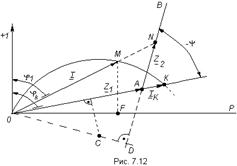Нахождение тока для любого значения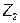

Для нахождения тока 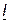по прямой АВ необходимо отложить вектор 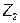в соответствующем масштабе 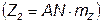. На диаграмме 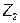- отрезок .

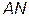Затем соединяем точк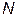и и 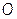между собой. Тогда вектор тока 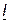будет являться отрезком 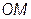. Точка 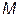- это точка пересечения отрезка 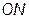с окружностью.

При изменении сопротивления 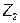от 0 до 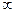точка 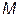(конец вектора 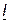) будет перемещаться от точки 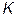до точки 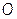по окружности.

Для нахождения активной мощности при соответствующем токе 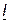необходимо из точки 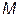опустить перпендикуляр до пересечения с прямой 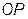(то есть параллельно оси +1). Тогда:

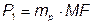
Реактивная мощность в этом случае представляет отрезок 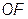, параллельный оси +j (на диаграмме не показана).

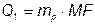
Полная мощность на входе четырёхполюсника: