Частное судейство.
Мини-процесс.
Посредничество.
Фигура посредника согласовывается сторонами. Посредническую процедуру можно предусмотреть в контракте. Посредник принимает активное участие. Решение, которое принято при проведении посреднической процедуры не является обязательным. Могут обратить ся в суд. Как правило во всех торговых палатах есть правила в отношении посредничества.
В странах общего права появился
Чаще всего используется я в Австралии. Должно быть письменное соглашение сторон. Если письменного соглашения нет, то одна из сторрон может обрутиься в торговую палату, палата обращается к конрагенту и спршивает согласие. В соответсвии с правилами формируется соответствующий состав. Прежде всего в отличии от арбитражного разбирательства, стороны направляются сотрудников, которые составляют комиссию. Возглавляет комиссию посредник в правила цюрихского мини-траила предусмотрено что спор должен быть рассмотрен в течении 30 дней. Обсуждается комиссией и они пытаются достигнуть разрешения спора. Решение выполняется добровольно.
|
|
|
Приблизительно такие же правила в бельгийском мини-траил.
В РФ такого способа разрешения спора вообще не предусмотрено.
Так же характерно для системы общего права. Для разрешения спора как правило избирается судья в отставке. Решение такого судьи носит обязательный характер для сторон. Он рассматривает по каким-то процессуальным правилам. Разница в том, что сами выбирают судью, а не назначается.
Иногда для разрешения споров могут создаваться экспертные комиссии, которые дают заключение как спор должен быть разрешен и сторон уже сами определяют, что им делать. Решение такой комиссии не обязательно для сторон.
В РФ среди альтернативных способов разрешения спора используют МКАС, но туда можно обратить ся только если одна из сторон спора- иностранное лицо. Российские ЮЛ могут обратиться в третейский суд.
В контракте при ответственности лучше предусмотреть убытки. В лизинге не забыть про то, что происходит с имуществом, переходит и выкупается, то необходимо предусмотреть как, в какой срок.
1. Деформации
1.1 Деформации и смещения
Следствием действия внешних сил может быть либо перемещение тела в пространстве как целого, либо его формы. Изменение формы – это, в сущности, изменение расстояния между различными точками в объеме тела, и именно такой феномен называется деформацией.
Деформацию, как изменение расстояния между двумя точками можно описать, рассматривая перемещение в пространстве двух соседних точек, отстоящих друг от друга на бесконечно малое расстояние.
|
|
|
Рассмотрим смещение любой точки 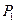 в теле, имевшей в декартовой системе фиксированные начальные координаты
в теле, имевшей в декартовой системе фиксированные начальные координаты 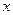 ,
,  ,
, 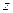 . После деформации новые координаты точки
. После деформации новые координаты точки 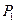 будут
будут 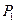
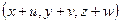 . Смешение точки
. Смешение точки 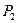 , расположенной бесконечно близко к точке
, расположенной бесконечно близко к точке 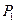 и имевшей до деформации координаты
и имевшей до деформации координаты 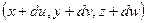 , будет
, будет 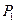
 . Следовательно, величинами относительных смешений являются
. Следовательно, величинами относительных смешений являются  ,
, 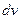 ,
, 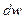 . Учитывая, что
. Учитывая, что  ,
,  ,
, 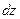 бесконечно малы, получаем
бесконечно малы, получаем
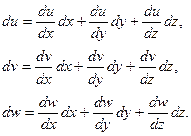 (19)
(19)
Тензор деформации определяется как
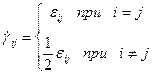 (20)
(20)
или
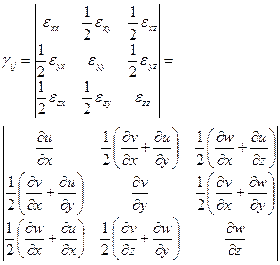 (21)
(21)
1.2 Специальные случаи деформации – одноосное растяжение и простой сдвиг
Одноосное растяжение и коэффициент Пуассона
Эксперименты показывают, что при одноосном растяжении образец пертерпевают изменения в продольном направлении. Связь между изменениями размеров в продольном и поперечном направлении может бытьустановлена исходя из простых геометрических соображений. Эта связь отражает некоторые внутренние свойства материалов. Количественным отражением этой связи служитотношение поперечного сжатия к продольной деформаци, и это свойство материала называют коэффициэнтом Пуассона.
Пусть радиус поперечного сечения растягиваемого стержня в исходном состоянии равняется r0, а длина l0. В результате растяжения длина стрежня увеличилась на Δl, а радиус уменьшился на Δr. Тогда, согласно определению, коэффициент Пуассона μ вычисляется следующим образом:
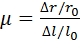 (22)
(22)
Теперь нетрудно подсчитать, каким образом изменяется объем тела вследствии деформации. Относительное изменение объема ΔV/V0 равно
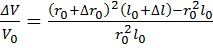 (23)
(23)
где V0 =πr02l0 – начальный объем образца (в недеформированном состоянии).
Для малых деформаций, когда Δl << l0 соответственно r << r0 выполняется следующее оотношение:
 (24)
(24)
Последнее соотношение ясно показывает, что коэфициент Пуассона представляет собой меру объемных изменений при малых деформациях. Видно также, что что деформация происходит без изменения объема тела ир только тогда, когда μ = 0,5. Для реальных твердых тел μ < 5, а во многих случаях коэффициент Пуассона лежит в диапазоне 0,3-0,35. Это означает, что одноосное ратяжение сопровождается увеличением объема тела. Только для резин μ ≈ 0,5, то есть они деформируются без изменения объема.
Коэффициент Пуассона не может быть больше 0,5, так как в противном случае гидростатическое сжатие приводило бы к увеличению объема, что физически абсурдно. В то же время отрицательные значения коэффициента Пуассона не противоресят никаким фундаментальным принципам. Значения μ < 0 показывает, что при одноосном растяжении поперечные размеры образца увеличиваются. Такая ситуация действительно возможна для пен.
Использование коэффициента Пуассона позволяет предложить следующий общий метод разложения тензора малых деформаций dij на сферническую и девиаторную части. Если λ << 1 и деформация при одноосном растяжении равна ε*, то тензор dij, определяемый формулой (23), может быть представлен следующим образом:
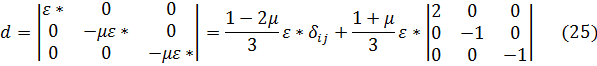
Структура этой суммы подобна структуре тензора напряжений, разлагаемого на две составляющие.
Более детальный анализ формулы (23) показывает однако, что для больших деформаций уравнение (24) неприменимо, и правило μ = 0,5 в общем случае не соответствует условию постоянства объема. Действительно, если сохранить неизменным определение коэффициента Пуассона по формуле (22), то исходя из уравнения (23), условие неизменности объема ΔV=0 при одноосном растяжении запишется следующим образом:
1-2μ(1+ε)+ μ2ε(1+ε) =0 (26)
Если ε << 1, то туравнение (26) сводиться к обычному условию μ = 0,5, но в общем случае это не так.
Простой сдвиг и чистый сдвиг
Движение любых жидкостей представляет собой скольжение соседних слоев относительно друг друга. Это случай простого сдвига. Простой сдвиг также может осуществляться при некоторых схемах деформирования твердых тел, например при кручении длинных труб и проволоки.
|
|
|
Двумерный (плоский) сдвиг элемента тела в области малых деформаций и в общем случае произвольных деформаций показан на рисунке 6 a и b. Смещение u1 происходит вдоль направления, обозначенного стрелкой. Градиент смещения du1/dx2 определяется величиной угла наклона γ.
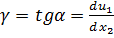 (27)
(27)
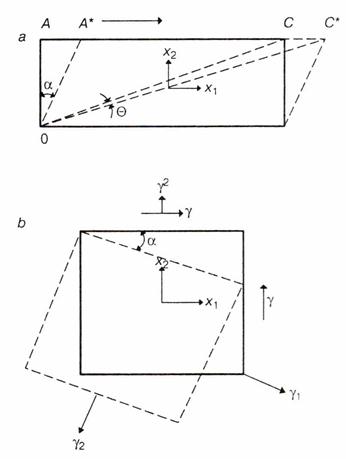
Рис.6 Малые (a) и большие (b) деформации припростом сдвиге
Длина линейного элемента ориентированного до начала деформации в направлении x2 изменяется при сдвиге. Пэтому имеет место еще одно смещение u2. Оно обусловлено изменением длины сегмента ОА. В результате длина сегмента становиться равной ОА*. Относительное изменение длины равно
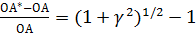 (28)
(28)
Величина γ = du1/dx2 при простом сдвиге определяет все компоненты тензора деформаций εij. Согласно определению εij его компоненты выражаются следующим образом:
ε12 = ε21 = 1/2γ; ε22 = 1/2γ2 (29)
Этот тензор играфически иллюстрируется на рис 6 (b).Компоненты тензора εij обозначены стрелками.
2.3. Скорость деформации
Рассмотрим кинематику процесса деформирования, т.е. скорость перехода из одного состояния в другое. Иными словами, производную тензоре деформация необходимо рассматривать по времени 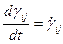 Компоненты тензора скорости деформации
Компоненты тензора скорости деформации 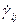 выражаются через производные компонент скорости
выражаются через производные компонент скорости 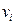 по координатам
по координатам 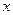 ,
,  ,
, 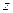 :
:
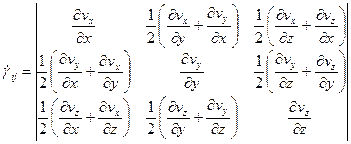 (30)
(30)
Совокупность производных компонент скорости vi по координатным осям есть градиент скорости 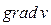 :
:
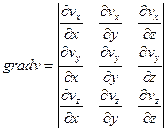 (31)
(31)
Тогда связь между тензором 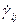 и
и 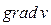 может быть представлена следующим образом:
может быть представлена следующим образом:
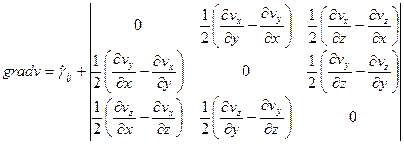 (32)
(32)
Второе слагаемое в правой части этого равенства отвечает вращательному движению элементов среды без деформации. Отсюда следует, что наличие градиента скорости в материале еще не означает его деформации, поскольку определенные комбинации компонент 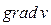 приводят к вращению среды как целого без ее деформации. Возможны случаи, когда
приводят к вращению среды как целого без ее деформации. Возможны случаи, когда 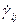 и
и 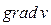 численно равны. Так, при одноосном растяжении
численно равны. Так, при одноосном растяжении 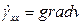 . При простом сдвиге
. При простом сдвиге 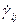 и
и 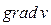 различаются на величину 1/2:
различаются на величину 1/2:
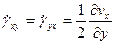 ,
, 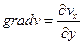 (33)
(33)
Инварианты тензора скорости деформации строятся аналогичноинвариантам тензора напряжений. Так, для плосконапряженного деформирования
|
|
|
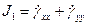 ,
, 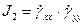 (34)
(34)
 2014-02-02
2014-02-02 687
687






