Целочисленное линейное программирование

Таблица 5.18

Таблица 5.13

Таблица 5.12

Пн По	В1	В2	В3	Запасы
А1	2	4	3
А2	1	5	4
Потребности				58 #50

Это открытая транспортная задача, в которой .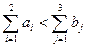

Введем фиктивный пункт отправления А₃ с запасом 8 (табл. 5.13)

Пн По	В1	В2	В3	Запасы
А1	2	4	3
А2	1	5	4
А3	0	0	4
Потребности				58=58

Получилось закрытая транспортная задача. Решим ее методом
потенциалов (табл. 5.14, 5.15, 5.16, 5.17).

Таблица 5.14 Таблица 5.15

Пн По	В1	В2	В3	Запасы	αi		Пн По	В1	В2	В3	Запасы	αi
А1	2	4	3 3				А1	2 2	4	5 3
А2	3 1	5	4				А2	1	5	4
А3	-1 0	1 0	0		-3		А3	-3 0	1 0	0		-4
Потре бности				58=58			Потре бности				58=58
βj							βj

Таблица 5.16 Таблица 5.17

Пн По	В1	В2	В3	Запасы	αi		Пн По	В1	В2	В3	Запасы	αi
А1	0 2	4	3				А1	0 2	4	3 18
А2	1	5	4				А2	1	5	4 4
А3	-3 0	1 0	0		-3		А3	-4 0	0	0		-4
Потре бности				58=58			Потре бности				58=58
βj							βj

В таблице 5.17 - оптимальный план перевозок для закрытой транспортной задачи. Опускаем перевозки из фиктивного пункта А₃,
получим оптимальный план для открытой транспортной задачи (табл.5.18).

f_min = 2•4 + 18•3 + 15•1 + 15•5 = 152

Потребность пункта В₂ удовлетворена не полностью.

Пн По	В1	В2	В3	Запасы
А1	2	4	3 18
А2	1	5	4
Потре бности

Целочисленное программирование – раздел математического программирования, рассматривающий оптимизационные задачи, в которых все или некоторые переменные могут принимать только целые значения. Как правило, требование целочисленности переменных значительно усложняет задачу. Целочисленное программирование систематически изучается с 1956 года, но и сейчас этот раздел находится в стадии развития.

6.1. Общая постановка задачи целочисленного линейного программирования (ЗЦЛП).

Мы будем рассматривать только полностью целочисленные задачи, в которых требование целочисленности наложено на все переменные. Общий вид такой ЗЦЛП отличается от ЗЛП только тем, что ко всем переменным предъявляется требование целочисленности. В частности, в каноническом виде ЗЦЛП ставится так:

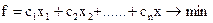(6.1)

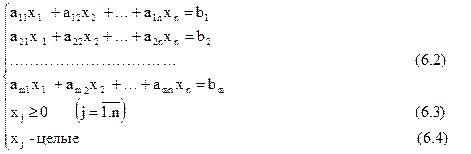
Для ЗЦЛП используется та же терминология, что и для ЗЛП: целевая функция, допустимое решение, оптимальное решение и т.д. Если в ЗЦЛП отбросить требование целочисленности, то получится так называемая ослабленная задача. Ослабленная задача является ЗЛП, в то время как ЗЦЛП таковой не является. Дело в том, что требование целочисленности переменных нельзя записать в виде линейного ограничения. Аналитически его записать можно. Действительно, обозначим через [a] целую часть числа а, т.е. наибольшее целое, которое не больше а. Например, [3.4] =3; [-7.2]= -8. Требование целочисленности переменной x_j можно записать так: x_j -[x_j ] =0. Однако это соотношение не является линейным. Таким образом, нельзя сказать, что ЗЦЛП – частный случай ЗЛП – она вообще не является ЗЛП.

Для ЗЦЛП не существует такого универсального эффективного метода решения, каким является симплекс-метод для ЗЛП. Из точных методов решения отметим метод отсечения Гомори и комбинированный метод ветвей и границ. Суть этого комбинированного метода мы изложим.

На практике большинство ЗЦЛП решается приближенно. При этом часто приходится разрабатывать приближенный метод, учитывающий специфические особенности задачи.

Приведем примеры ЗЦЛП.