Движение жидкой частицы

Рассмотрим движение бесконечно малой жидкой частицы, имеющей первоначальную форму параллелепипеда (рис.3.5)

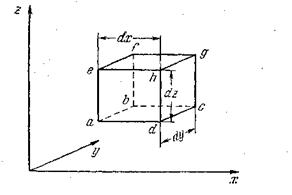
Рис.3.5

В отличие от твердого тела жидкая частица при своем движении может сильно деформироваться.

Грани этой частицы, имеющей в начале движения форму прямого параллелепипеда с ребрами dx, dy, dz, с течением времени могут скашиваться и растягиваться (рис.3.6, 3.7)

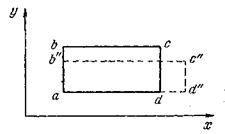Рис.3.6. Угловая деформация граней Рис. 3.7. Линейная деформация граней.

Пусть составляющие скорости движения частицы в точке 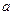(рис.3.5) суть Ux, Uy, Uz, тогда составляющие скорости в точке b равны

в точке d

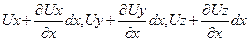
и в точке е

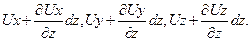
Скашивание ребра ab частицы за бесконечно малое время dt, которое вызывается разностью компонентов скорости в точках 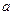и b (рис.3.6), характеризуется смещением точки b, равным

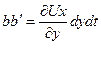
Относительное смещение или угловая деформация

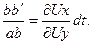
Скашивание ребра 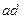приводит к угловой деформации

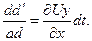
Ввиду того, что угловые деформации за время dt незначительны, угол наклона грани можно считать равным тангенсу этого угла. Полное скашивание прямого угла в точке 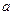в этом случае равно

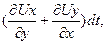
а скорость соответствующей угловой деформации

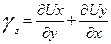. (3.10а)

Индекс z указывает на то, что рассматривается деформация частицы в плоскости XУ, перпендикулярной к оси Z; в остальных двух плоскостях скорости скашивания координатных углов равны, очевидно,

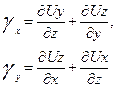
(3.10б)

(3.10в)

Используя те же угловые смещения граней частицы, можно определить угловые скорости ее вращения. Поскольку направления вращения ребер 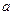b и ad противоположны, средняя угловая скорость вращения частицы в целом около оси Z составляет

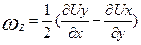. (3.11а)

Для остальных двух осей вращения имеем соответственно

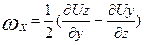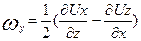, . (3.11б)

Вектор угловой скорости вращения 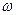, составляющие которого суть 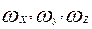, носит название завихренности, или вихря скорости. Его величина определяется следующим равенством:

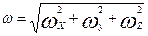. (3.12)