2015-03-22
3207
В кинематике твердого тела доказывается, что в общем случае движение твердого тела в каждый момент времени складывается из поступательного перемещения и вращения вокруг некоторой оси (мгновенной оси вращения). Движение жидкой частицы гораздо сложнее, так как она в процессе движения еще и деформируется.
Рассмотрим в момент времени t движение бесконечно малой частицы жидкости (рис. 2.3). Пусть точка М частицы имеет скорость, проекции которой равны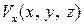 
, 
, 
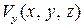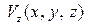в системе координат OXYZ. Поместим в эту точку начало системы координат Mx 1 y 1 z 1.
Тогда в некоторой точке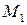 
на поверхности частицы с координатами 
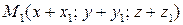проекции скорости равны
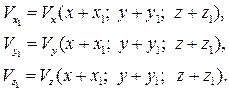
Применим к полученной системе разложение в ряд Тейлора и, сохраняя только величины первого порядка малости (члены с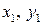 
и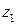 
в степени не выше первой), получим следующее:
,
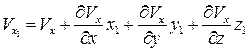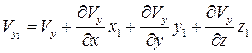, (2.6)
.
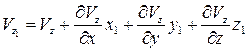Преобразуем эти выражения: прибавим к правой части первого уравнения (2.6) величины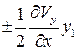 
и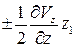 
и перегруппируем члены:
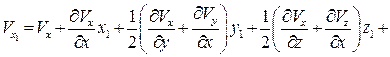
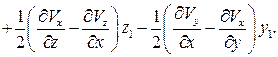
Аналогично преобразуем второе и третье уравнения системы (2.6), дополнениями которых являются члены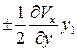 
, 
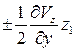и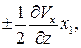 
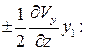
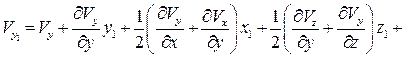
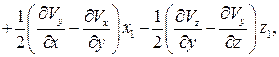
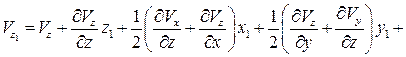
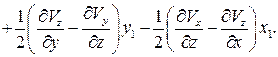
Введем следующие обозначения:
, 
, 
,
, 
,
, 
.
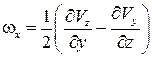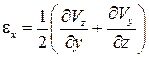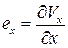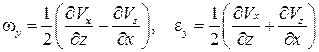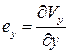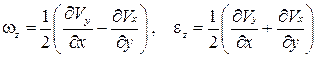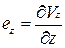Тогда преобразованные выражения (2.6) для проекций вектора скорости можно записать следующим образом:
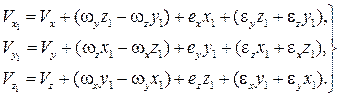(2.7)
Введем функцию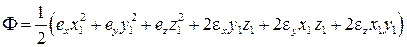 
. Ее производные по координатам 
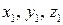равны
, 
,
.
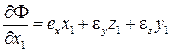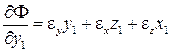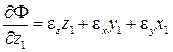Теперь перепишем систему уравнений (2.7) с помощью функции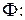 
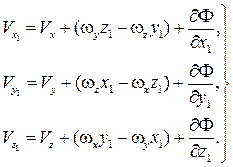(2.8)
Выясним физический смысл каждого из слагаемых, входящих в выражения (2.8):
1. 
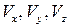– это проекции скорости поступательного движения рассматриваемой частицы в пространстве твердого тела.
2. 
, 
, 
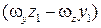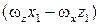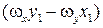– проекции угловой скорости вращения частицы жидкости (как твердого тела) вокруг мгновенной оси, проходящей через точку М. Такое вращательное движение называется вихревым движением, а компоненты угловой скорости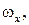 
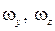– компонентами вихря. Угловая скорость вращательного движения равна 
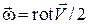, где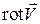 
– так называемый ротор или вихрь вектора скорости:
= 
– 
,
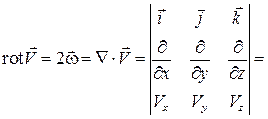
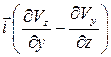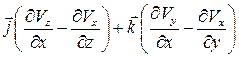где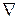 
– операция градиента, т. е. 
.
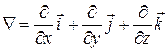Физически неравенство нулю значения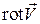 
в какой-либо точке потока означает, что в этой точке имеет место вращение элементарного объема. Составляющие угловой скорости вращения равны
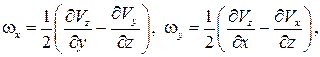
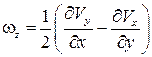. (2.9)
3. 
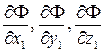. Смысл этих слагаемых можно выяснить, исходя из простых физических соображений. Ясно, что жидкая частица при движении деформируется, и эти члены представляют собой не что иное, как скорости деформации частицы. Поясним это на примере.
Пусть бесконечно малая частица имеет в момент t форму прямоугольного параллелепипеда. Рассмотрим его проекцию на плоскость XY (рис. 2.4, прямоугольник МВDС). Компоненты скорости в точке М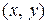 
равны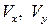 
. Составляющие скорости в точках В 
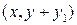и С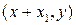 
с точностью до малых первого порядка можно представить в виде
, 
,
, 
,
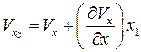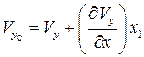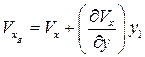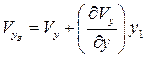или, так как рассматривается перемещение точек С и В относительно точки М, то
, 
,
, 
.
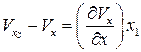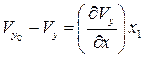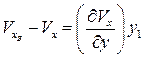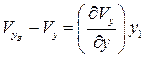Очевидно, что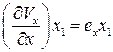 
и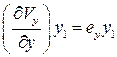 
есть скорости линейной деформации ребер прямоугольника. 
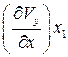и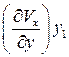 
указывают на поворот ребер МС и МВ, т. е. скорости деформации скашивания прямоугольника в некоторый косоугольник. Ребро МС поворачивается со скоростью 
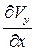, МВ – со скоростью 
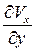, т. е. скорость изменения прямого угла ВМС складывается из угловых скоростей вращения ребер МС и МВ и, следовательно, представляет собой сумму 
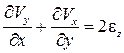. Аналогичные рассуждения можно провести для других проекций параллелепипеда.
Отсюда следует, что 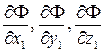– компоненты скорости деформации жидкой частицы. Следовательно, формулы (2.8) подтверждают следующее:
Элементарное перемещение частицы жидкости (газа) состоит из поступательного перемещения ее центра со скоростью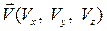 
, вращения относительно некоторой оси, проходящей через этот центр с угловой скоростью 
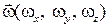, и деформационного движения, характеризуемого функцией 
.
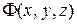Эта теорема (первая теорема Гельмгольца) является основной теоремой кинематики жидкой среды. То есть движение жидкой частицы в общем случае можно разложить на поступательное движение, вращательное движение и движение от деформации, которая состоит из линейной деформации и деформации скашивания. Такое разложение наиболее правильно с динамической точки зрения, так как оно разделяет движения, происходящие от сил разной природы.
