(сначала ген.совокуп., потом выборочная). Объем выборки: N, n. Альтернативные (качественные) признаки: численность едини совокупности, обладающих признаком: M, m. Доля единиц, обладающих изучаемым признаком: p=M/N; w=m/n. Дисперсия: 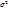 = p(1-p)=pq;
= p(1-p)=pq; 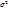 = w(1-w). Среднее квадратическое отклонение:
= w(1-w). Среднее квадратическое отклонение: 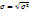 . Количественные признаки: Среднее значение признака:
. Количественные признаки: Среднее значение признака: 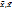 =
= 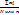 . Дисперсия:
. Дисперсия: 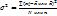 . Среднее квадратическое отклонение:
. Среднее квадратическое отклонение: 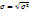 . Ошибки выборки возникают в связи с тем, что выборочная совокупность отличается от генеральной. Существует 2 вида ошибок выборки: 1) Ошибки регистрации (случайные и систематические); 2) Ошибки репрезентативности – возникают в результате того, что выборочная совокупность не полностью отражает генеральную. Ошибка выборочного наблюдения – разность между величиной параметра в генеральной совокупности и его величиной в выборочной совокупности.
. Ошибки выборки возникают в связи с тем, что выборочная совокупность отличается от генеральной. Существует 2 вида ошибок выборки: 1) Ошибки регистрации (случайные и систематические); 2) Ошибки репрезентативности – возникают в результате того, что выборочная совокупность не полностью отражает генеральную. Ошибка выборочного наблюдения – разность между величиной параметра в генеральной совокупности и его величиной в выборочной совокупности. 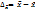 . Ошибка наблюдения зависит от способа отбора и процедуры выборки. *есть на почте, потом вставить*. Средняя ошибка выборки:
. Ошибка наблюдения зависит от способа отбора и процедуры выборки. *есть на почте, потом вставить*. Средняя ошибка выборки: 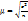 - выражает среднее квадратическое отклонение выборочной средней от генеральной средней. Зависит от: 1) колеблемости признака в генеральной совокупности (
- выражает среднее квадратическое отклонение выборочной средней от генеральной средней. Зависит от: 1) колеблемости признака в генеральной совокупности (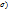 ; 2) числа отобранных единиц (n). Чем больше единиц, тем меньше ошибка. Средняя ошибка выборки показывает, какие возможны отклонения характеристик выборочной совокупности от соответствующих характеристик выборочной совокупности характеристик в генеральной совокупности. О величине этой ошибки судят и определенной вероятностью, на величину которой указывает коэффициент доверия (t) – характеризует вероятность того, на какую величину генеральная средняя будет отличаться от выборочной средней. Таким образом, зная выборочную среднюю величину признака (
; 2) числа отобранных единиц (n). Чем больше единиц, тем меньше ошибка. Средняя ошибка выборки показывает, какие возможны отклонения характеристик выборочной совокупности от соответствующих характеристик выборочной совокупности характеристик в генеральной совокупности. О величине этой ошибки судят и определенной вероятностью, на величину которой указывает коэффициент доверия (t) – характеризует вероятность того, на какую величину генеральная средняя будет отличаться от выборочной средней. Таким образом, зная выборочную среднюю величину признака (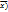 и предельную ошибку выборки (
и предельную ошибку выборки (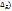 , можно поределить пределы, в которых заключена генеральная средняя.
, можно поределить пределы, в которых заключена генеральная средняя. 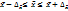 . Средняя ошибка выборки альтернативного признака:
. Средняя ошибка выборки альтернативного признака: 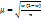 . Предельная ошибка выборки альтернативного признака:
. Предельная ошибка выборки альтернативного признака: 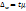 . Границы:
. Границы: 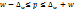
41. Определение необходимого объема выборки осуществляется исходя из способа отбора. *тоже на почте, потом вставить*
 2014-02-05
2014-02-05 829
829








