Основные определения. Понятие множества является понятием первичным, т.е

Алгебра множеств

Понятие множества является понятием первичным, т.е. не определяемым через другие элементарные понятия. Множество состоит из элементов. Отношение включения элемента х в множество М обозначается Запись 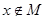означает, что элемент х не принадлежит множеству М. Существует несколько способов задания множеств, применение которых обусловлено контекстом. Ниже перечислены способы основные способы задания множеств:

· Перечислением элементов, которые указываются через запятую и заключаются в фигурные скобки. Например, запись M={x,y,z} означает трехэлементное множество. Очевидно, такой способ применим для не слишком больших множеств.

· Указанием характеристического свойства, например, M={x | xÎ N (N – множество натуральных чисел), 2<x<7}. Очевидно, эта запись указывает множество {3,4,5,6}.

· Графически с помощью диаграмм Эйлера-Венна. Диаграмма Эйлера-Венна представляет собой выпуклую самонепересекающуюся кривую, очерчивающую область, в которой находятся все элементы множества.

· Аналитически с помощью операций на множествах.

· С использованием характеристической функции, которая позволяет представлять множество двоичным словом.

Два множества называются равными, если они состоят из одних и тех же элементов. При этом порядок перечисления этих элементов не существен. Обозначение равенства множеств: А=В. Обозначение неравенства множеств А ¹ В.

Между множествами существует два вида отношений включения:
Ì - отношение истинного включения; А Ì В Û "х: х Î А Þ х Î В и А ¹ В;

Í - более общий тип включения, АÍ В Û "х: х Î А Þ х Î В или А=В.

На основании определения отношения включения «Í», определение тождества множеств можно записать следующим образом: А = В Û А Í В и В Í А. Это определение используется для доказательства тождества множеств.

Множество называется конечным, если число его элементов равно некоторому натуральному числу, и бесконечным, если такого натурального числа не существует. Общим свойством всех множеств является из кардинальное число или мощность. Мощность множества А обозначается |A|. Мощность конечного множества равна числу его элементов. Мощность бесконечного множества зависит от типа множества. Бесконечные множества бывают счетные и несчетные. Самым простым из счетных множеств является множество натуральных чисел N = {1,2,…,n,…}. Его мощность обозначается специальным символом алеф-нуль a₀. Примером несчетного множества является множество действительных чисел R, его мощность называется мощностью континуума, обозначается С.

Множество, не содержащее элементов, называется пустым множеством, обозначается Æ.

Универсумом называется множество, из элементов которого строятся все другие множества, обозначается I.

Множество всех подмножеств данного конечного множества называется булеаном этого множества. Булеан множества А обозначается Р(А), его мощность |P(A)| = 2^|A|.

При задании множеств с использованием характеристической функции необходимо задать конечный универсум М и упорядочить его элементы. При задании любого подмножества N множества М каждому его элементу характеристическая функция ставит в соответствие 0 или 1 в соответствии с правилом:

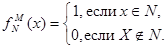
Например, если M={2,3,4,5}, то множество N = {3,5} с использованием характеристической функции будет записано как (0101), пустое множество – (0000), само множество М – (1111).

Основные операции над множествами:

Объединением множеств А и В называется множество АÈВ = {x | "x: xÎ A или xÎ B}.

Пересечением множеств А и В называется множество А Ç В = {x | "x: xÎA и x Î B}.

Разностью множеств А и В называется множество A\B = {x | "x: x Î A и x Ï B}.

Разность универсума I и множества А называется дополнением А и обозначается `А или ù А.

Симметрической разностью множеств А и В называется множество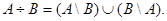

Универсум с заданными на нем подмножествами, операциями и отношениями образуют алгебру Кантора (алгебру множеств).