Функция yп(t) является решением однородного дифференциального уравнения, поэтому устойчивость системы однозначно зависит от корней характеристического уравнения.
Если корни действительные, т.е. si = ai, то
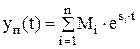 ,
,
где n – число корней характеристического уравнения (степень уравнения), Mi – коэффициенты, si – корни.
Каждая составляющая функции yп(t) является экспонентой вида
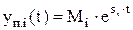 .
.
При этом если si > 0, то экспонента расходится ( ), если si < 0 - сходится (
), если si < 0 - сходится (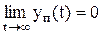 ).
).
В случае, если среди корней характеристического уравнения имеются комплексные, т.е. si = ai ± j×wi, то каждой паре комплексно сопряженных корней соответствует составляющая
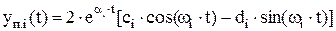 ,
,
где ci и di – коэффициенты. Данная составляющая представляет собой синусоиду, сходящуюся при ai < 0 и расходящуюся при ai > 0 (при ai = 0 синусоида имеет постоянную амплитуду).
Для устойчивости системы необходимо и достаточно, чтобы все составляющие функции yп.i(t) стремились с течением времени к нулю. Если хотя бы одна составляющая функции расходится, то расходится и вся функция, т.е. система в данном случае неустойчива.
Из сказанного следует, что для устойчивости линейной системы необходимо и достаточно, чтобы корни характеристического полинома имели отрицательные действительные части.
Критерий, определяющий устойчивость системы по значениям корней характеристического полинома, получил название корневого.
Для определения устойчивости необходимо путем приравнивания знаменателя передаточной функции (характеристического полинома) к нулю получить характеристическое уравнение и его корни. Корни характеристического уравнения могут быть как действительные, так и комплексные и для наглядности могут быть изображены на комплексной плоскости (плоскости корней).
На рисунке 1.42 символом  обозначены корни некоторого уравнения.
обозначены корни некоторого уравнения.
Виды корней характеристического уравнения:
- действительные: положительные (корень 1), отрицательные (корень 2) и нулевые (корень 3);
- комплексные: комплексные сопряженные (4) и чисто мнимые (5).
По кратности корни бывают: одиночные (1, 2, 3), сопряженные (4, 5): si = a ± jw и кратные (6) si = si+1 = …
Корневой критерий формулируется следующим образом:
 Линейная АСР устойчива, если все корни характеристического уравнения лежат в левой полуплоскости (она называется также областью устойчивости). Если хотя бы один корень находится на мнимой оси, которая является границей устойчивости, то говорят, что система находится на границе устойчивости. Если хотя бы один корень находится в правой полуплоскости (независимо от числа корней в левой), то система является неустойчивой.
Линейная АСР устойчива, если все корни характеристического уравнения лежат в левой полуплоскости (она называется также областью устойчивости). Если хотя бы один корень находится на мнимой оси, которая является границей устойчивости, то говорят, что система находится на границе устойчивости. Если хотя бы один корень находится в правой полуплоскости (независимо от числа корней в левой), то система является неустойчивой.
Иными словами, все действительные корни и действительные части комплексных корней должны быть отрицательны. В противном случае система неустойчива.
Пример. Передаточная функция системы имеет вид
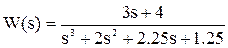 .
.
Характеристическое уравнение s3 + 2s2 + 2,25s + 1.25 = 0 имеет три корня:
s1 = -1; s2 = -0,5 + j; s3 = -0,5 - j.
Действительные части всех корней отрицательны, следовательно, система устойчива. ¨
 2014-02-02
2014-02-02 3560
3560








