2014-02-02
618
Пример
Пример
х+(х2-х)+(х3-х2)+…+(хn-xn-1)+… E=[0,1]
u1(x)=x, un(x)=xn-xn-1 при n³2. Sn(x)=x+x2-x+x3-x2+…+xn-xn-1=xn; S(x)=lim Sn(x)= lim xn={0 при хÎ[0,1[ и 1 при x=1.
На каждом отрезке 0,a при a>1 сх-ть равномерная:("хÎ[0, a])[|rn(x)|=|Sn(x)-S(x)|=|xn-0|=xn£a]Þ 0£
|rn(x)|£ an, а т.к. lim an=0, то и lim 
|rn(x)|=0. На всём отрезке Е=[0,1] сх-ть неравомерная. В самом деле:("хÎЕ) [|rn(x)|=|Sn(x)-S(x)|={xn, x Î [0,1[ и 0,x=1], поэтому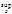 
|rn(x)|=1.
m ("хÎЕ) [|rn(x)|£1 Þ 1-верх. граница множества {|rn(x)|:xÎE}, 1-e - не м.б. верхней границей: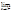 
|rn(x)|= 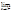хn=1, значит при хÎЕ достаточно близких к 1 будет ||rn(x)|-1|<eÞ|rn(x)|>1-eÞ1- наим. из всех верхних границ: 1=
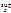|rn(x)| l. Значит lim 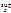|rn(x)| =lim 1=1¹0
Теор Критерий Коши равномерной сходимости функ. ряда.
Функ. ряд (1) сх-ся на мн.Е равномерно Û ("e>0)($ne):("m>n>ne)("xÎE)[|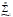 
uk(x)|<e]
1 Пусть ряд (1) сх-ся равномерно. Зададим e>0 и положим e1=e/2, для него по Опр 5.2. ($ ne): ("n> ne)("хÎЕ)[|Sn(x)-S(x)|<e1].Þ ("m>n>ne)("хÎЕ)[|Sn(x)-S(x)|<e1]. Поэтому |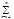
uk(x)|= |Sm(x)-Sn(x)|= |(Sm(x)-S(x))+(S(x)-Sn(x))|£ |Sm(x)-S(x)|+|S(x)-Sn(x)|< e1+e1=e.
Ü Пусть выполнен критерий Коши. При конкр. хÎЕ это означает выполнение кр. Коши для числового ряда, значит ч.р.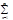 
un(x), хÎЕ сх-ся к некот. числу S(x). Это означает, что ф.р. (1) поточеч. сх-ся к некот. сумме S(x). Осталось пок-ть, что это сх-ть равномерная. Зададим e>0 и возьмём 0<e1<e, для него запишем кр. Коши: ($n0): (" m>n>n0) ("хÎЕ)[ |
uk(x)|= |Sm(x)-Sn(x)|<e1]. Зафиксируем здесь n0 и х. И рассмотрим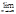 
(при этом всегда ост-ся m>n и потому |Sm(x)-Sn(x)|<e1 сохр. во всём процессе стремления m к ¥). В пределе получим ($n0): (" m>n>n0) ("хÎЕ) [ 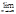|Sm(x)-Sn(x)|£e1], но 
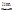|Sm(x)-Sn(x)|=| 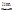Sm(x) -
|
|
|
lim(n®+µ)Sn(x)|=(*Sn(x)=const*)= |S(x)-Sn(x)|£e1Þ |Sn(x)-S(x)|<e. Подчёркнутое означает, по Опр.5.2., что ряд (1) сх-ся равномерно на множестве Еg. Из кр. Коши получается след. дост. признак равномерной сх-ти.
19. Теор Признак Вейерштрасса о равномерной сх-ти.
Если существует полож, числовой, сх-ся ряд 
an (4), т.ч. ("n)("хÎЕ) [|uk(x)|£an] (мажорирующий ряд, мажоранта), то ряд (1) сх-ся на множестве Е абсолютно и равномерно.
1 |uk(x)|£an при всех хÎЕ следует, согл. признаку сравнения сх-ся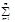 
|un(x)|Þ 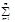un(x) сх-ся абсолютно на множестве Е. Для ряда (4) выполнен крит. Коши: ("e>0)($ne):("m>n>ne)
[| |<e], но
Опр. Функ. ряд для которого сущ. мажоранта, наз-ся мажорирующим. По док-му ряд, мажорируемый на Е сх-ся абс-но и равномерно на мн-ве Е.
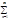
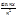("n)("xÎ]-¥,+¥[)[|
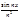|£1/n2]
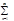
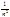- сх-ся и потому мажорантой на ]-¥,+¥[. След-но данный ряд сх-ся абс. и равномерно на ]-¥,+¥[.
20. Свойства равномерно сх-ся рядов.
Известно, что конеч. сумма непрер-х функций, есть непр-я функ-я. Такую сумму можно почленно инт-ть, конеч. сумму диф-ть.
Для суммы функ. ряда это не так, например члены ряда x+(x2-x)+…+(xn-xn-1)+… непрер-ны на Е=[0,1], а сумма ряда S(x)={0, xÎ[0,1[ и 1,x=1 разрывна в т. х=1.
|
|
|
Теор о непрерывности суммы ряда.
Если все члены un(x) функ. ряда u1(x)+u2(x)+…+un(x)+…(1) непрерывны на Е и ряд сх-ся равном. на Е, то S(x) непрер-на на Е.1Надо пок-ть, что("х0ÎЕ) [S(x)Îc{x0}Û("e>0)($d>0): ("xÎE,|x-x0|<d)[S(x)-S(x0)<e]]. Зададим e>0 и положим e1=e/3. Ввиду равном. сх-ти ряда для e1: ($n0):(" n>n0) ("хÎЕ)[|Sn(x)-S(x)|<e1] (2). В частности |Sn(x0)-S(x)|<e1 (3). Зафиксируем один номер n>n0 и рассм. функ-ю Sn(x)= u1(x)+…+un(x). Как конеч. сумма непр-х ф-ий она непр-на на Е. В частности Sn(x)Îc{x0}. Значит ($d>0):("xÎE,|x-x0|<d)[Sn(x)-Sn(x0)<e1] (4). Теперь из 2,4,3 получим |S(x)-S(x0)|=| (S(x)-Sn(x))+ (Sn(x)-Sn(x0))+(Sn(x0)-S(x0))|£ |Sn(x)-S(x)|+|Sn(x)-Sn(x0)|+|Sn(x0)-S(x0)|£e1+e1+e1=eg
21. Теор об интегрировании ряда.
Если все члены un(x) функ. ряда (1) непрер-ы на [a,b] и ряд сх-ся на [a,b] равномерно, то его можно почленно инт-ть по любому отрезку [x1,x2]Ì[a,b].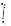 
S(x)dx=
un(x)dx= 
un(x)dx (ряд полученный почленным инт-ем ряда (1) сх-ся и его сумма = интегралу от суммы ряда (1) или интеграл от суммы ряда = сумме ряда).
1 Т.к. все un(x)Î[a,b], то существует un(x)dx=аn (числа); ввиду равном. сх-ти ряда по Теор.6.1. сумма ряда S(x)Î[a,b]Þ сущ-ет S(x)dx=s (число) и ост. док-ть, что числ. ряд =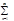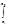un(x)dx сх-ся к s, т.е. lim 
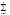ak=s. Зададим e>0 и положим e1=e/(х2-х1)>0. Ввиду равном. сх-ти ряда (1) ($n0):(" n>n0) ("хÎ[a,b])[|Sn(x)-S(x)|<e1]Þ ("хÎ[x1,x2])[|Sn(x)-S(x)|<e1]. |
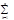ak-s|= |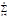
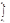uk(x)dx - 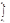S(x)dx| = (*для конеч. суммы Sò=òS*) =| 
(
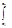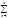uk(x) – S(x))dx| =|
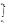(Sn(x)-S(x))dx|£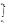|Sn(x)-S(x)|dx< 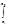e1dx= e1(x2-x1)=e. Т.о. ("e>0)($n0):(" n>n0)[ |
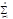ak-s|<e]Þ lim 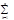ak=s g
22. Теор о дифференцируемости ряда.
Если все члены un(x) ф.р. (1) сходящиеся на [a,b] (необяз. равном.) непрер. диф-мы на [a,b] (un¢(x)Îc[a,b]), а ряд из производных: u1¢(x)+u2¢(x)+…+un¢(x)+…(5) равномерно сх-ся на [a,b], то ряд (1) можно почленно дифф-ть в любой т.хÎ[a,b]: S¢(x)=( 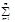un(x))¢= 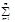un¢(x) (производная суммы ряда равна сумме производных).o По условию ряд (5) равном. сх-ся на [a,b] к некот. сумме s(х): 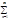un¢(x)= s(х) и по Теор.6.2. (*благодаря непрерывности un¢(x) на [a,b]*) ряд (5) можно почленно инт-ть по отрезку [a,x] где х любая точка из [a,b]: 
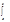s(t)dt=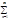 
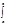un¢(t)dt, здесь
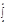un¢(t)dt = un(t)½
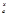= un(х)- un(а). Поэт. 
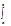s(t)dt= 
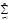(un(х)- un(а)). Поскольку 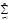un(х) сх-ся к S(x) по условию, в частности un(а) сх-ся к S(a), по Теор Олин-х опер-ях с рядами 1.10.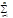 
(un(х)- un(а))= 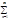un(х) -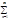un(а) = S(x)-S(a), а след-но 
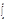s(t)dt= S(x)-S(a). По Теор 6.1. сумма s(х) ряда (5) с непрерывными членами равномерно сх-ся на [a,b] непрер-на на [a,b]. Поэт. можно применить Т. о диф-ии инт-ла с перем. верх. пределом: (
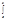s(t)dt)¢х=s(х), значит s(х)= S¢(x) - 0Þ S¢(x)= s(х)= 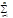u¢n(х)g
Теор об ограниченном множителе.
Если все члены ряда (1) равном. сх-ся на Е умножить на ф-ию ограниченную на Е, то равном. сх-ть ряда (1) на Е сохр-ся.1Пусть("хÎЕ)[|f(x)}£M]. Рассм. ряд f(x)u1(x)+f(x)u2(x)+.. …+f(x)un(x)+…(6). Для равном. сх-ся ряда (1) вып-ся кр. Коши: ("e>0)($ne):("m>n>ne)("xÎE)[|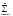 
uk(x)|<e].
Тогда("xÎE)[ |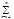f(x)uk(x)|=|f(x)|×|
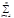uk(x)|£M×|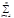uk(x)|<M×(e/M)=e]. Поэт. для ряда (6) ок-ся выполненым кр-ий Коши: ("e>0)($ne):("m>n>ne)("xÎE)[| 
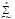f(x)uk(x)|<e] и потому он сх-ся равном. на Е.
23. Радиус сход-ти, интервал сход-ти, область сход-ти.
C0+C1(x-a)+C2(x-a)2+...+Cn(x-a)n+...==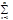
Cn(x-a)n (1), где Сn и а - действительные числа, наз-ся степенным рядом с центром х=а. Заменой x=х-а такой ряд приводится к виду (вместо x пишем х):
С0+С1х+С2х2+...+Сnхn+...=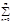
Сnхn (2) поэтому можно ограничится изучением ряда (2). Ряд (2) всегда сходится к точке х=0: S(0)=C.
24. Т-ма Абеля
Если степенной ряд (2) сходится в точке х0¹0, то он абсолютно сходится при |х|<|х0|, т.е. на ]-|x0|,|x0|[; если он расходится в точке х0 ¹0, то расходится при |х|<|x0|, т.е. на ]-¥,-|x0|[ и ]|x0|,+¥[.
1 Если сходится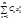 
, то lim 
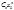и сходящаяся последовательность {
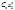} ограничена: ("n)[| 
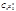|£M]Þ("n)[|Cn|£ M/|x0n|. Если |x|<|x0|, то |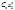|=|Cn|×|x|n£ M/|x0n|×|x|n= M(|x|/|x0|)n= M×qn, где q=|x|/|x0|<1. Из сходимости геометрического ряда 
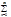Mqn (q<1) по признаку сравнения следует сход-ть 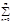|Сnxn|, т.е. абсолютная сход-ть ряда (2) при рассматриваемом |х|<|x0|. Eсли ряд (2) расходится в точке х0¹0, то при |х|>|x0| он не может сходится, т.к. по доказанному он бы сходился в точке х0Þ при |х|>|x0| ряд (2) расходится g
|
|
|
Т-ма о радиусе сходимости
Для каждого степенного ряда (2)сущ-ет неотрицательное число RÎ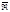
такое, что на ]-R,R[ ряд абсолютно сходится, а вне отрезка [-R,R] (т.е. на ]-¥,-R[ u ]R,+¥[) расходится.
1 Если (2) ходится в единственной точке х=0, то полагают R=0 (в точке х=0 ряд (2) сходится абсолютно: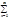
|Сn0n|=|C0|). Пусть сущ-ют 
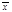¹0, в которых ряд сходится, назовем их точками сход-ти. Мн-во модулей точек сход-ти обозначим Х={|
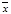|}, и пусть R=Sup X. Т.к. имеются точки 
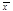¹0, т.е. |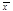|>0, то Sup X>0, т.е. R>0. Пусть |х|<R, тогда |х| меньшее чем Sup X не может быть верхней границей мн-ва Х и потому найдется |
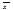|ÎХ такой, что |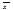|>|x|. Из сход-ти (2) в точке 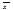по т-ме Абеля следует абсолютная сход-ть ряда в точке х. Таким образом ряд (2) абсолютно сходится на ]-R,R[. В частности если R=+¥, то на ]-¥,+¥[. Пусть R<+¥, т.е. R-конечное число, тогда если |х|>R, то х не может быть точкой сход-ти, т.к. для всех точек сход-ти 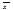имеем |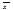|£ Sup X=R Þ при |х|>R, т.е. при хÎ]-¥,-R[ u ]R,+¥[ ряд расходится. g
Число R наз-ся радиусом сход-ти степенного ряда (2), ]-R,R[ -интервалом сходимости.
Замечание1.
Для степенного ряда (1) интервалом сход-ти явл-ся ]a-R,a+R[.
1 Если для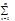 
Сnxn xÎ]-R,R[ Û -R< x <R, т.е. -R<x-a<R Û a-R< x <a+R g
Замечание2.
На концах интервала х=±R ряд (2) может сходится (абсолютно или не абсолютно) и расходится, поэтому область сход-ти степенного ряда с точностью до граничных точек совпадает с интервалом сходимоси Þ чтобы найти область сход-ти степенного ряда достаточно найти интервал сход-ти, а сход-ть в граничных точках х=±R исследовать непосредственной подстановкой этих точек в ряд (2). Что же касается интервала сход-ти ряда (2), то он совпадает с интервалом сход-ти ряда из модулей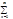
|Cnxn|, т.к. внутри интервала сходимости ряд (2) сходится абсолютно, т.е. сходится ряд 
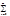|Cnxn|, а вне интервала сход-ти ряд (2) расходится и тем более расходится ряд из модулей. Таким образом дело сводится к нахождению интервала сход-ти положительного ряда из модулей, а к этому положительному ряду можно применять признаки сход-ти положительных рядов.
|
|
|
Пример: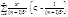 
Решение: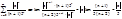 
1) если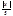 
<1, то ряд сходится.
2) если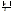 
>1, то ряд расходится.
3) если |х|=5 Þ х=5 или х=-5 Þ
Þ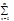 
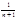расходится; или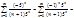 
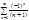- по признаку Лейбница сходится условно (не абсолютно).
25. Свойства степенных рядов.
Т-ма о равномерной сход-ти степенного ряда.
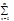anxn = a0+a1x+a2x2+...+anxn+... (1). Степенной ряд (1) сходится равномерно в каждом замкнутом промежутке, расположенным внутри области сход-ти степеного ряда (1).
1 Считаем, что R>0. Если промежуток (-R*,R*) замкнутый и целиком лежащий в интервале ]-R,R[, то обязательно найдется -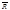
и 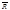, расположенные соответственно в ]-R,R*[ и ]R*,R[ Þ
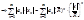. Eсли 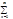|an|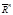
- cходится, то|an|
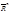£MÞ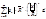
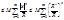. Обозначим 
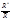=q < 1. Мы получим ряд из членов убывающей геометрической прогрессии. Воспользуемся признаком Вейерштрасса M·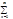
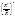
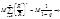сходится ряд равномерно на [-R*,+R*] g
Пример: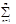 
n!xn.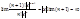
.Этот ряд расходится всюду, кроме х=0.
26Одна из формул определения радиуса сход-ти R степенного ряда (основанная на признаке Даламбера):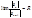 
1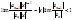
- сходится. 
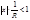(сходится)Þ |х|<R; |x|>R - расходитсяg
Замечание: В общем случае этот предел может не существовать.
8.2. Т-ма
Внутри интервала сход-ти сумма ряда (1) - непрерывная функция.
1 Т.к. члены степенного ряда (1) непрерывные функции, то согласно т-ме о непрерывности суммы ряда, ряд (1) явл-ся непрерывной функцией g
8.3. Т-ма об интегрируемости степенного ряда:
Пусть [x0,x1]Ì(-R,R), тогда
1)
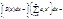
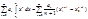(2)
2) Радиус сход-ти ряда (2), полученного после интегрирования равен радиусу сход-ти исходного ряда (1).
1 Пусть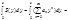 
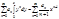(2*). Найдем радиус сход-ти ряда (2*). 
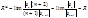g
8.4. Т-ма о дифференцируемости степенного ряда:
1) Внутри интервала сход-ти сумма степенного ряда S(x) - дифференцируемая функция, ряд можно почленно дифференцировать.
2)
Радиус сход-ти степенного ряда, полученного после дифференцирования, равен радиусу исходного ряда.
1) Согласно предыдущей т-ме ряд сходится равномерно, члены дифференцируемы и по т-ме о дифференцируемости ряда ряд (1) можно дифференцировать почленно.
2) Рассмотрим ряд вида (S(x))’= (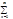anxn)¢=a1+2a2x+3a3x2+...+nanxn-1+..
Найдем радиус сход-ти этого ряда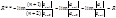 
g
27. Формула Тейлора. Т-ма
Пусть функция f(x) имеет непрерывные производные вплоть до (n+1)- го порядка включительно в некоторой окрестности точки х=а, тогда имеет место формула Тейлора:
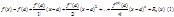. Rn(x) - остаточный член, который может быть представлен в виде: 
(2) - форма Лагранжа, где x-расположена между точками х и а. Другой вид: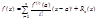
1 Построим вспомогательную функцию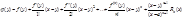
(3)
тогда j(а)=f(x)Þj(x)=f(x)+f `(x)(x-x)+..=f(x) Þ j(a)=f(x) и j(x)=f(x). Тогда по т-ме Ролля найдется точка x в которой j’(x)=0.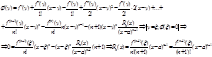 
получим (2) g
Замечания: 1) сущ-ют и другие представления Rn;
2) x=a+q(x-a), |q|£1.
28. Ряды Тейлора и Макларена.
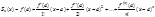; f(x)=Sn(x)+Rn(x) (6); f(x)-Sn(x)=Rn(x) (6¢). Потребуем, чтобы функция f(x) имела бесконечное число производных f(n)(x) в точке x=а и её окрестности. Получим: lim (f(x)-Sn(x))=lim Rn(x)=0 (7). Если lim Rn(x) сущ-ет и равен 0, то f(x)=lim Sn(x) (8) Þ 
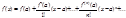(9) - ряд Тейлора. При а=0 получаем ряд Макларена:
.
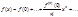Замечание Функция представлена в форме ряда Тейлора в том случае если Rn(x)®0.
Пример неразложимости функции в ряд Тейлора.
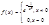. Т.к. 
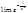=0, то функция f(x) непрерывная Þ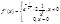 
Обозначим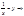 
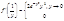. По правилу Лопиталя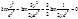 
Аналогичным образом устанавливается, что функция f(x) имеет бесконечно большое число производных и все они непрерывны на всей оси, включая точку х=0 и в точке х=0 обращаются в нуль.
"n=0,1,2... Sn(x)=0. f(x)=Sn(x)+Rn(x)ºRn(x) Þ Rn(x)- не стремится к нулю, то ряда Тейлора для этой функции не сущ-ет.
10.1. Т-ма о представимости степенных рядов рядом Тейлора.
Если функция f(x) представима степенным рядом f(x)=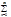an(x-a)n,
то этот степенной ряд явл-ся рядом Тейлора: f(x)=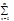 
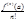(x-a)n, т.е. an= 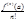(11). И такое разложение единственно и коэфициенты нах-ся по формуле (11).
1 f `(x)=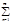 
nan(x-a)n-1, f ``(x)= 
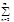(n-1)nan(x-a)n-2,..., f(i)(x)=
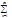(n-i+1)(n-i+2)...nan(x-a)n-i,
Þ f(n)(a)=n!an Þ (11). Докажем единственность: предположим противное и пройдя всю цепочку рассуждений получим все коэфициенты, которые определяются по формуле (11). g
29. Т-ма (достаточный признак сход-ти степенного ряда к функции f или представимости в виде ряда Тейлора).
Пусть |f(n)(x)|£C=const "n=0,1,1... в некоторой замкнутой окрестности точки аÎХ, тогда функция f представима степенным рядом Тейлора.
1 Имеем |Rn(x)|£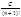
(x-a)n+1®0 при n®¥. Применяя признак Даламбера получаем, что ряд
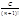(х-а)n+1 сходится g
30.Разложение основных элементарных функций в степенные ряды.
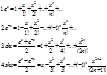5. f(x)=cosx, f(0)=1,
(cosx)`=-sinx(0)=0,
(cosx)``(0)=(-cosx)(0)= -1
(cosx)```(0)=sinx(0)=0
(cosx)````(0)=cosx(0)=1,...
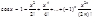
Т.к. cosx-четная функция, то сохраняются только четные степени.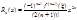 
. Т.к. sin и cos по модулю £1, то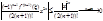 
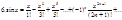Остаточный член оценивается точно так же как cos. Указанные ряды можно использовать лишь в окрестности точки х=0, при удалении от х=0 апроксимация будет резко ухудшаться.
7.f(x)=ln(1+x)
ln(1+x)=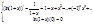 
Þ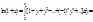
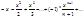ln(1+x)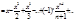 
8.f(x)=arctgx
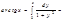
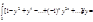
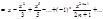
9. Биномиальное разложение.
f(x)=(1+x)a, a-любое действительное число.
f(0)=1; f `(0)=a(1+x)a-1=a;
f ``(0)=a(a-1)(1+x)a-2=a(a-1);
f ```(0)=a(a-1)(a-2)(1+x)a-3=
=a(a-1)(a-2);...;
f(n)(0)=(a-n+1)(1+x)a-n=(a-n+1).
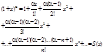Определяем остаточный член: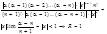
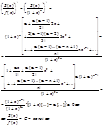Þ в точке х=0 S(x)=1 и f(x)=1 Þ
ÞC=1.
Некоторые применения степенных рядов в приближенных вычислениях.
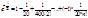e£0.001.
Применения для вычисления интегралов.
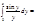
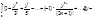
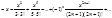
Следующий пример:
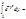интегралвероятностей=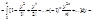
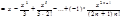
Примененение степенных рядов для решения дифференциальных уравнений с переменными коэффициентами.
y``=xy, y(0)=1, y`(0)=0
y(x)=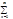anxn - предполагаемое решение; y`(x)= 
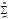nanxn-1,y``(x)=
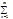(n-1)nanxn-2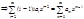 
а0=1 и а1=0 по условию. Приравниваем коэфициенты при равных степенях:
при x0 1*2a2=0
при х1 2*3а3=а0=1
при х2 3*4а4=а1=0
при х3 4*5а5=а2=0....
при хn-1 n(n+1)an+1=an-2
при xn (n+1)(n+2)an+2=an-1
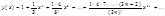
§11. Ряды Фурье.
Далее мы будем рассматривать глобальное разложение, то есть на конечном отрезке [a,b].
Определение. Понятие ортогонольных и нормированных систем ф-ий:
j(х), y(х) интегрируемые при хÎ[a,b], тогда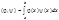 
(*) - cкалярное произведение.
для (*) вып-ся аксиомы ск-го произведения:
А.1 (j,y)=(y,j)
А.2 (lj,y)=(j,ly)=l(j,y), l=const
А.3 (j,y1+y2)=(j,y1)+(j,y2)
Определение: Функции j и y на [a,b] ортогональны если (j,y)=0, т.е.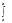 
j(х)y(х)dx=0.
Определение. Понятие нормированности: ||j||=
- норма (длина вектора).
Докажем, что норма обладает всеми св-вами длины:
||j||=[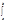
j2(x)dx]0.5
A.1 ||j||³0, ||j||=0 Û jº0
A.2 ||lj||=|lj||, "lÎR1
A.3 ||j1+j2||=||j1||+||j2||
Определения: Если для системы функций j1,j2,...,jn введено понятие нормы, то такая система наз-ся нормированной. Если норма каждого элемента пространства равна 1, то наз-ся нормированной на 1. Если система функций попарно ортогональна и нормированная на 1, то такая система наз-ся ортонормированной: ОН - ортонормированная система, если
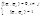; ОН Þ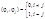
Пример: при xÎ[-p,p]
{1,cosx,sinx,cos2x,sin2x,...,
cosnx,sinnx}.
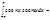
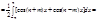
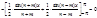. Аналогично 
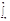sin(nx)sin(mx)dx=0;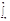sin(nx)cos(mx)dx=0. Найдем норму: ||cosnx||=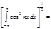
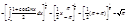. Аналогично ||sin(nx)||=
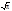.Получаем ОН систему:
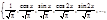
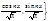
Ряд Фурье. Коэфициенты Фурье по ОН системе.
{j1(x),j2(x),...,jn(x)} - ОН система, т.е.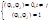 
. f(x)=
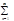fnjn(x) - ряд Фурье, где fn - коэфициенты. Умножим обе части этого уравнения на jm(x) и проинтегрируем:
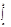f(x)jm(x)dx==
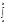jm(x)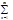 
fnjn(x)dx=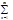fn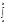jm(x)jn(x)dx=0 - когда m¹n. Когда m=n:
=fn(jn,jn)=fn=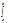
f(x)jn(x)dx Þ f(x) ~ 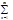(f,jn)jn(x)
Ряд Фурье для тригонометрических функций.
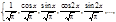
, f(x) ~
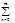(ancos(nx)+bnsin(nx)) (4)
где an=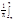
f(x)cos(nx)dx, bn=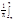f(x)sin(nx)dx, n=0,1,2,...
Определение: Функция наз-ся кусочно-непрерывной на данном отрезке, если этот отрезок можно разбить на конечное число интегралов, в каждом из которых функция непрерывна.
Т-ма Дирихле: Пусть f(x)
1)определена для всех хÎ[-p,p]
2)кусочно-непрерывная на [-p,p]
3)кусочно-монотонная на [-p,p]
4)ограничена на [-p,p], тогда она разложима в тригонометрический ряд Фурье (4). Если точка хÎ[-p,p] и в этой точки f(x) непрерывна, то сумма ряда
S(x)=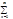(ancos(nx)+bnsin(nx))=f(x). Если точка х - точка разрыва, скачок, то S(x)=1/2 [f(x-0)+f(x+0)]
S(-p)=S(p)=1/2 [f(p+0)+f(p-0)]
Замечания: 1)поведение функции f за пределами [-p,p] может в корне отличаться от значения S.
2)если мы хотим разложить f на всей действительной оси, то соглас- но (4) мы должны продол- жить пе- риодическим образом с периодом 2p.
Пример: f(x)=x, xÎ[-p,p]
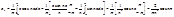
a0=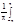
xdx=0
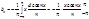
Разложение функций в тригонометрические ряды на произвольном промежутке.
Часто возникает задача разложения функций в тригонометрический ряд на произвольном промежутке
yÎ[a,b] (|a|,|b| < ¥,a < b)
x=ay+b; [-p,p] переходит в [a,b].
,
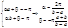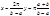m, f(ay+b)=f*(y); dx=ady, an=
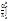f*(y)cosn(ay+b)dy
bn=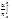
f*(y)sinn(ay+b)dy, f*(y)=
+
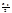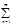(ancosn(ay+b)+bnsinn(ay+b))
Разложив cos и sin по формулам:
f*(y)=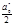
+
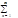(a*ncosnay+b*nsinnay), где нужно вычислить a*n, b*n и a*0.
Примеры: 1) a=0, b=L >0
x=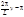
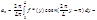
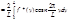
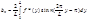
2) a= - L, b= L
x=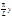
Разложение четных функций в тригонометрический ряд.
f(x)=f(-x), xÎR1
an=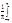
f(x)cosnxdx=
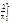f(x)cosnxdx
bn=0
f(x)=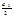 
+
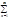ancosnx - разложение по косинусам.
Разложение нечетных функций в тригонометрический ряд.
f(x)= - f(-x); a0=0, an=0
f(x)=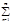 
bnsinnx
bn=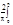
f(x)sinnxdx
- разложение по синусам.
Примеры: 1) f(x)=x
a0=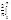
1dx=2; an=
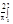1cosnxdx=0
f(x)=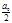 
=1
2) Функция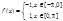 
bn=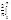1sinnxdx=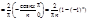
Разложение функций в ряд по синусам в несимметричном промежутке (0, L).
f(x), xÎ[0, L]. Доопределим функцию на промежутке [-L,0] (нечетным образом)
1. В ряд по синусам.
f(x)=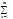 
bnsin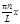
, где
bn=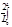
f(x)sin
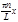dx
2. В ряд по косинусам (четным образом).
f(x)=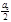 
+
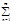ancos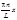
, где
an=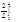
f(x)cos
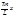dx
Пример: по синусам
f(x)=x, xÎ[0,1], L=1
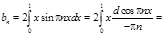
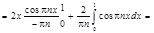
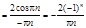
1. Предмет, метод, система и принципы земельного права
Земельное право - отрасль права, регулирующая общественные отношения, возникающие в сфере предоставления, использования и охраны земель. Регулирование отношений по использованию и охране земли осуществляется исходя из представлений о земле как о природном объекте, охраняемом в качестве важнейшем составной части природы, основы жизни и деятельности народов.
Предмет земельного права составляют земельные правоотношения. Земельные отношения в соответствии с п.1 ст.3 Земельного Кодекса РФ - это общественные отношения по использованию и охране земель в Российской Федерации как основы жизни и деятельности народов РФ. В предмет земельного права входят элементы административных, имущественных, финансовых и других отношений. Земельные отношения регулируются как нормами земельного, так и нормами гражданского законодательства. К земельным отношениям применяется также законодательство по использованию и охране недр, вод, лесов, животного мира и иных природных объектов, охране окружающей среды, охране атмосферного воздуха и охране объектов культурного наследия народов Российской Федерации
Под методом отрасли права понимается способ, при помощи которого государство обеспечивает нужное ему поведение. Метод земельного права - совокупность способов, средств, приемов воздействия норм данной отрасли права на поведение участников общественных отношений. Способы могут быть запрещающими, обязывающими, разрешающими, т.е. дозволительными.
Нормы, которыми устанавливаются запреты или должное поведение (обязанности), называются императивными. Диспозитивные нормы предполагают предоставление свободы субъектам правоотношений, субъекты могут сами устанавливать границы своего поведения. Для метода земельного права характерно сочетание императивных и диспозитивных норм. При этом императивные нормы занимают значительный удельный вес в содержании земельно-правовых норм.
Природа земельных отношений в процессе проведения земельной реформы существенно изменилась: в значительной своей части эти отношения стали имущественными, что связано с включением земель в перечень объектов недвижимого имущества. В частности, это относится к большой группе земельных отношений, где земля выступает в качестве объекта гражданско-правовых сделок.
Указанные выше обстоятельства служат основанием и для соответствующих изменений в методе регулирования земельных отношений: наряду с императивным методом всё более значение играет диспозитивный метод.
Системой отрасли земельного права является объективно существующее упорядоченное единство земельно-правовых институтов, последовательно расположенных в соответствии с их значимостью в регулировании земельных отношений и содержанием этих отношений. Система земельного права состоит из двух частей: общей части, содержащей правовые нормы и положения, относящиеся ко всей отрасли в целом, и особенной части, охватывающей нормы об особенностях правового регулирования отдельных категории земель.
В основе системы земельного права, как и любой другой правовой отрасли лежат юридические нормы, которые, группируясь по определенным признакам, образуют институты земельного права и отрасль земельного права. К особенностям земельного права можно отнести его двухуровневость.
Земельное право имеет два уровня: уровень федеральный и уровень субъектов Федерации (региональный), что основано на принципе совместного ведения земельным законодательством со стороны Российской Федерации и её субъектов. Двухуровневая система земельного законодательства - специфика его современной системы.
Земельное право можно рассматривать не только в качестве отрасли права, но и отрасли законодательства, правовой науки и учебной дисциплины.
Земельное право как отрасль законодательства - это система законов и иных нормативных правовых актов, в которых закреплены норма гражданского права.
Земельное право как наука - это учение о земельном праве, т.е. совокупность суждений, знаний, теорий, взглядов, идей о земельном праве.
Дисциплина «Земельное право» - курс лекций, семинарских занятий, целью которых является получение студентами необходимых знаний о действующих нормативных правовых актах, регулирующих предмет земельного права, и навыков применения данных знаний в практической деятельности.
