Дисперсия альтернативного признака

В ряде случаев возникает необходимость измерить вариацию альтернативного признака, т.е. признака, принимающего два взаимоисключающих значения.

Среднее значение альтернативного признака равно

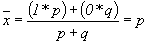
т.к. (сумма долей единиц, обладающих и не обладающих данным признаком, равна единице).

Дисперсия альтернативного признака определяется следующим образом:

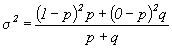
Подставив в формулу дисперсии вместо 1-p значение q=1-p, получим:

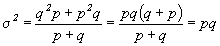
Таким образом, 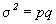, т.е. дисперсия альтернативного признака равна произведению доли единиц, обладающих данным признаком, и доли единиц, им не обладающих.

Если значения 0 и 1 встречаются одинаково часто, т.е. p=q, то дисперсия достигает своего максимума pq=0,25.