Лекция №6 предмет и задачи математической статистики

Выводы

Основные понятия и термины

Вопросы для самопроверки

1. Начертите модель кругооборота товара и денег. Какие допущения делаются при построении модели кругооборота товара и денег?

2. Какие функции выполняют домашние хозяйства и фирмы на рынке товаров и рынке ресурсов?

3. Охарактеризуйте движение товаров и ресурсов, движение денег в модели кругооборота товара и денег.

4. Какие выводы, характеризующие организацию рыночной экономики, можно сделать на основании модели кругооборота товара и денег?

5. По каким критериям можно сгруппировать все рынки?

6. Что такое инфраструктура рынка и что она в себя включает?

Натуральное хозяйство, товарное хозяйство, товар, общественное разделение труда, принцип сравнительных преимуществ, деньги, абсолютная ликвидность, функции денег, масштаб цен, товарные деньги, бумажные деньги, кредитные деньги, электронные деньги, пластиковые карточки, рынок, контракт, кругооборот товара и денег, инфраструктура рынка.

1. Существование рынка предполагает, что производство носит товарный характер, т.е. продукты производятся для продажи, обмена. Условиями существования товарного хозяйства являются: общественное разделение труда, которое базируется на принципе сравнительных преимуществ способности отдельного производителя производить товар с относительно меньшими альтернативными издержками; экономическая обособленность товаропроизводителей на базе частной собственности и обмен как форма связи между обособленными и самостоятельными товаропроизводителями.

2. Деньги – это все то, что принимается продавцом для оплаты товаров и услуг. Отличительная особенность денег – их абсолютная ликвидность. Сущность денег проявляется в их функциях. Деньги выполняют функции средства обращения, меры стоимости и средства накопления. История денег знает их три основных вида: товарные деньги, бумажные деньги и кредитные деньги. Современные наличные деньги представляют собой долговые обязательства центральных банков, безналичные – долговые обязательства коммерческих банков в отношении их вкладчиков.

3. Рыночная экономика – это экономическая система, базирующаяся на частной собственности и непосредственных связях между покупателем и продавцом, координируемых главным инструментом рынка – ценой. Основные черты рыночной экономики: равноправие всех форм собственности, экономическая свобода, всеобщность рынка, контрактный характер рыночных отношений, экономическая ответственность субъектов рынка, конкуренция, свободное ценообразование.

К достоинствам рыночной экономики можно отнести: высокую способность к оперативному удовлетворению разнообразных потребностей людей, повышению качества товаров и услуг; гибкость и высокую адаптивность к изменяющимся условиям; максимальное использование достижений и стимулирование научно-технического прогресса; невозможность хронического товарного дефицита и др.

4. Рыночная организация экономики схематично может быть представлена в виде модели кругооборота товара и денег. На рынке товаров домашние хозяйства выступают в роли покупателей, а фирмы в качестве продавцов; на рынке ресурсов – наоборот: фирмы – покупатели факторов производства, домашние хозяйства – их продавцы. Один контур модели характеризует движение товаров и ресурсов в натуральном выражении, другой – встречное движение денежных платежей. Общая сумма всех расходов в экономике в целом равна общей сумме получаемых доходов.

Рыночная экономика представляет собой совокупность огромного числа разнообразных рынков, которые в зависимости от экономического назначения объектов рыночных отношений, по пространственному признаку, степени развитости конкуренции, объему продаж, степени соблюдения законности и т.п. могут быть объединены в отдельные группы. Необходимым условием нормального функционирования рынков является наличие рыночной инфраструктуры – совокупности отраслей, систем, фирм, опосредующих акты купли-продажи, совершаемые на рынке.

Основные задачи математической статистики. Определение законов распределения случайных величин на основе экспериментальных данных.

1. Предмет и задачи математической статистики.

Математической статистикой называется наука, занимающаяся методами обработки опытных данных, полученных в результате наблюдений над случайными явлениями. Любой такой результат можно представить как совокупность значений, принятых в результате n опытов какой-то случайной величиной или системой случайных величин. Поэтому дальнейший материал излагается на языке случайных величин.

Предмет математической статистики составляют методы регистрации, описания и анализа статистических экспериментальных данных, получаемых в результате наблюдения массовых случайных явлений.

К основным задачам математической статистики относятся:

Ø Задача определения закона распределения случайной величины по статистическим данным.

Теоретически при достаточно большом числе опытов свойственные изучаемым случайным величинам закономерности будут осуществляться сколь угодно точно. На практике мы всегда имеем дело с ограниченным количеством экспериментальных данных; в связи с этим результаты наших наблюдений и их обработки всегда содержат больший или меньший элемент случайности. К методике обработки экспериментальных данных следует предъявить такие требования, чтобы она, по возможности, сохраняла типичные, характерные черты наблюдаемого явления и отбрасывала все несущественное, второстепенное, связанное с недостаточным объемом опытного материала. В связи с этим возникает задача сглаживания или выравнивания статистических данных, представления их в наиболее компактном виде с помощью простых аналитических зависимостей.

Ø Задача проверки правдоподобия гипотез.

Ставится она так: в нашем распоряжении имеется совокупность опытных данных. Спрашивается, противоречат ли эти данные той или другой гипотезе? Например, гипотезе о том, что случайная величина X распределена по закону с плотностью f(x). В результате проверки правдоподобия гипотезы может быть сделан один из выводов: 1) отбросить гипотезу, как противоречащую опытным данным; 2) не отбрасывать гипотезу, считать ее приемлемой.

Ø Задача определения неизвестных параметров распределения.

Как на основании статистических данных, оценить, хотя бы приближенно, интересующие нас характеристики, например математическое ожидание, дисперсию и средне квадратическое отклонение случайной величины, над которой велись наблюдения? С какой точностью, при данном количестве опытов, будут оцениваться эти характеристики?

2. Простая и упорядоченная статистическая совокупность.

Совокупность наблюденных значений случайной величины Х представляет собой первичный статистический материал, подлежащий обработке. Такая совокупность называется «простой статистической совокупностью» или «простым статистическим рядом». Обычно простая статистическая совокупность оформляется в виде таблицы, в первом столбце которой стоит номер опыта, а во втором – наблюденное значение случайной величины. Если значения случайной величины расположить в взрастающем порядке, то мы получим упорядоченную статистическую совокупность

3. Статистическая функция распределения.

Статистической функцией распределения случайной величины Х называется частота события Х<х в данном статистическом материале

F*(x)=P*(X<x)

Для того чтобы найти значение статистической функции распределения при данном х, достаточно подсчитать число опытов, в которых величина Х приняла значение, меньше чем х, и разделить на общее число n произведенных опытов.

Статистическая функция распределения любой случайной величины – прерывной или непрерывной – представляет собой прерывную ступенчатую функцию, скачки которой соответствуют наблюденным значениям случайной величины и по величине равны частотам этих значений. При увеличении числа опытов n, согласно теореме Бернулли, при любомх частота события Х<х приближается (сходится по вероятности) к вероятности этого события. Следовательно, при увеличении n статистическая функция распределения F*(x) приближается (сходится по вероятности) к подлинной функции распределения случайной величины Х.

Если Х – непрерывная случайная величина, то при увеличении числа наблюдений n число скачков функции F*(x) увеличивается, сами скачки уменьшаются и график функции F*(x) неограниченно приближается к плавной кривой F(x) – функции распределения величины Х.

4. Статистический ряд.

Разделим весь диапазон наблюденных значений Х на интервалы или «разряды» и подсчитаем количество значений m_i, приходящееся на каждый i-ый разряд. Это число разделим на общее число наблюдений n и найдем частоту, соответствующую данному разряду:

p_i*=m_i/n

Сумма частот всех разрядов очевидно, должна быть равна единице.

Построим таблицу, в которой приведены разряды в порядке их расположения вдоль оси абсцисс и соответствующие частоты. Эта таблица называется статистическим рядом:

Ii	x1;x2	x2;x3	...	xi;xi+1	...	xk;xk+1
pi*	p1*	p2*		pi*		pk*

Здесь I_i– обозначение i–го разряда; x_i;x_i+1– его границы; p_i*– соответствующая частота; k– число разрядов.

Если значение случайной величины находится в точности на границе двух разрядов, то можно (чисто условно) считать данное значение принадлежащим в равной мере к обоим разрядам и прибавлять к числам m_i того и другого разряда по 0.5.

Число разрядов, на которые следует группировать статистический материал, не должно быть слишком большим (тогда ряд распределения становится невыразительным, и частоты в нем обнаруживают незакономерные колебания); с другой стороны, оно не должно быть слишком малым (при малом числе разрядов свойства распределения описываются статистическим рядом слишком грубо). Практика показывает, что в большинстве случаев рационально выбирать число разрядов порядка 10 – 20. Длины разрядов могут быть как одинаковыми, так и различными. При выборе равных интервалов разбиения диапазона изменения случайной величины оптимальная длина интервала может быть определена по оптимальному количеству интервалов в соответствии таблицей:

n
k

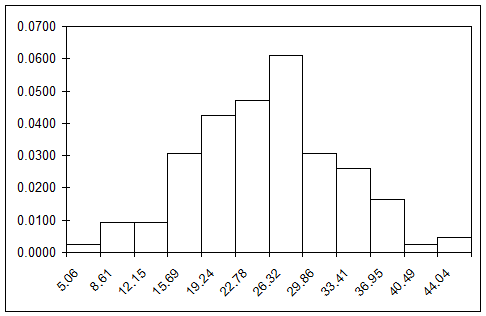
5. Гистограмма.

Статистический ряд часто оформляется графически в виде гистограммы. Гистограмма строится следующим образом. По оси абсцисс откладываются разряды, и на каждом из разрядов как на основании строится прямоугольник, площадь которого равна частоте данного разряда. Для построения гистограммы нужно частоту каждого разряда разделить на его длину и полученное число взять в качестве высоты прямоугольника. В случае равных по длине разрядов высоты прямоугольников пропорциональны соответствующим частотам. Из способа построения гистограммы следует, что полная площадь ее равна единице.

Очевидно, при увеличении числа опытов можно выбирать все более и более мелкие разряды; при этом гистограмма будет все более приближаться к некоторой кривой, ограничивающей площадь, равную единице. Нетрудно убедиться, что эта кривая представляет собой график плотности распределения величины Х

6. Числовые характеристики статистического распределения.

Каждой числовой характеристике случайной величины Х соответствует ее статистическая аналогия. Для математического ожидания случайной величины аналогией является среднее арифметическое наблюденных значений случайной величины:

где x_i– значение случайной величины, наблюденное в i–м опыте, n– число опытов.

Эта характеристика называется статистическим средним случайной величины.

Согласно закону больших чисел, при неограниченном увеличении числа опытов статистическое среднее приближается (сходится по вероятности) к математическому ожиданию. При достаточно большом n статистическое среднее может быть принято приближенно математическому ожиданию. При ограниченном числе опытов статистическое среднее является случайной величиной, которая, тем не менее, связана с математическим ожиданием и может дать о нем известное представление.

Подобные статистические аналогии существуют для всех числовых характеристик. Будем обозначать эти статистические аналоги теми же буквами, что и соответствующие числовые характеристики, но снабжать их значком *.

Рассмотрим, например, дисперсию случайной величины. Она представляет собой математическое ожидание случайной величины :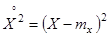

Если в этом выражении заменить математическое ожидание его статистической аналогией – средним арифметическим, мы получим статистическую дисперсию случайной величины Х:

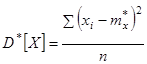
где m_x*=M*[X]– статистическое среднее.

Аналогично определяются статистические начальные и центральные моменты любых порядков:

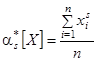
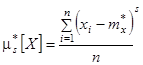
Все эти определения полностью аналогичны определениям числовых характеристик случайной величины. С той разницей, что в них везде вместо математического ожидания фигурирует среднее арифметическое. При увеличении числа наблюдений, очевидно, все статистические характеристики будут сходиться по вероятности к соответствующим математическим характеристикам и при достаточном n могут быть приняты приближенно равными им.

Нетрудно доказать, что для статистических начальных и центральных моментов справедливы те же свойства, которые были выведены для математических моментов. В частности, статистический первый центральный момент всегда равен нулю:

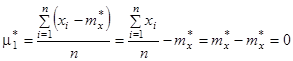
Соотношения между центральными и начальными моментами также сохраняются:

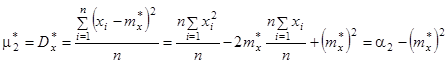
При очень большом количестве опытов вычисление характеристик по приведенным выше формулам становится чрезмерно громоздким, и можно применить следующий прием: воспользоваться теми же разрядами, на которые был расклассифицирован статистический материал для построения статистического ряда или гистограммы, и считать приближенно значение случайной величины в каждом разряде постоянным и равным среднему значению, которое выступает в роли «представителя» разряда. Тогда статистические числовые характеристики будут выражаться приближенными формулами:

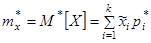
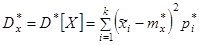
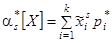
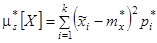
где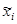– «представитель» i-го разряда, p_i*– частота i–го разряда, k – число разрядов.

Как видно, эти формулы полностью аналогичны формулам, определяющим математическое ожидание, дисперсию, начальные и центральные моменты дискретной случайной величины Х, с той только разницей, что вместо вероятностей в них стоят частоты, вместо математического ожидания – статистическое среднее, вместо числа возможных значений случайной величины – число разрядов.