Операции отрицания

Пусть множество значений функций принадлежности 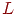является линейно упорядоченным множеством с наименьшим 0 и наибольшим 1 элементами. Примером 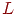может служить интервал вещественных чисел 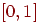, шкала лингвистических оценок (например, L={"неправдоподобно", "малоправдоподобно", "средняя правдоподобность", "большая правдоподобность", "наверняка"}, шкала балльных оценок и др.

Определение. Операцией отрицания на 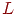называется функция 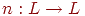, удовлетворяющая следующим условиям:

(О1) ;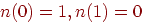

(O2) .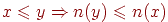

В зависимости от выполнения на 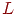дополнительных условий, рассматриваются следующие типы отрицаний:

· Строгое отрицание: ;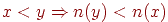

· Квазистрогое отрицание: ;

· Инволюция: ;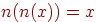

· Обычное отрицание: ;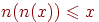

· Слабое отрицание: .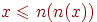

Слабое отрицание называется также интуиционистским отрицанием. Элемент 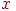из 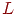будет называться иволютивным элементом, если 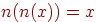, в противном случае он будет называться неиволютивным. Отрицание будет называться неиволютивным, если 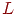содержит неиволютивные по этому отрицанию элементы.

Элемент 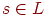, удовлетворяющий условию 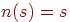, называется фиксированной точкой. Этот элемент будет центральным элементом (фокусом) 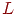. Очевидно, что если фиксированная точка существует, то она единственна.

Отрицание 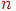называется сжимающим в точке 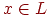, если выполнено условие

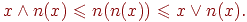
Отрицание называется сжимающим на 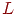, если оно сжимающее в каждой точке множества .

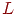Отрицание 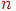называется разжимающим в точке 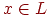, если выполнено условие

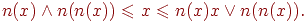
Отрицание называется разжимающим на 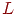, если оно является разжимающим в каждой точке множества .

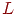Теорема Для любого отрицания 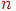любая точка 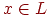является либо сжимающей, либо разжимающей.

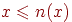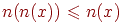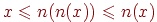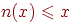Доказательство Пусть , тогда из условия (О2) получим , откуда следует либо , либо . Аналогично, из получаем 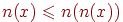, и, следовательно, либо 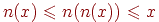, либо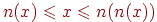

Следствие Элемент 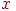является иволютивным тогда и только тогда, если он одновременно сжимающий и разжимающий.

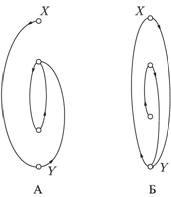
Используя математические методы, можно доказать, что элементы, порождаемые сжимающими и разжимающими отрицаниями в точках, представляют собой спирали, соответственно "закручиваемые внутрь" или "раскручиваемые наружу". Эти спирали либо бесконечные, либо в конечном случае имеют петлю на конце, состоящую из двух элементов, которые для сжимающих отрицаний могут совпадать, образуя неподвижную точку отрицания. Спирали, порождаемые разными элементами, либо вложены друг в друга, либо совпадают, начиная с некоторого элемента.

На рис. 8.1 даны примеры сжимающего и разжимающего в точке 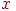отрицания. Элементы 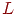представлены вершинами соответствующего графа и упорядочены снизу вверх, в частности, . Элементы y порождаются элементами 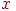так, что 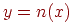для рис. 8.1(А) и 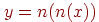для рис. 8.1(Б).