СТО. Ковариантная формулировка основного закона динамики материальной точки. Сила Минковского.
Инерционные свойства частиц описываются массой покоя этой частицы (m0).четырех-вектор импульса.
▼ По определению pα=m0uα (26). Естественным релетивистским обобщением II закона Ньютона является следующее уравнение: 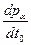 =Fα (27), Fα-некоторый четырех-вектор.
=Fα (27), Fα-некоторый четырех-вектор.
▼ Fα-называется силой Минковского. Запишем в координатах 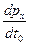 =
=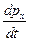
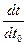 =
=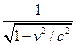
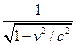
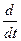
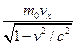 =Fx.
=Fx.
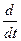
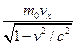 =Fx
=Fx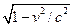 (28); v<<c. Мы потребуем, чтобы в правой части (28) стояла обычная сила F, тогда: ▼ Компоненты четырех-вектора силы:
(28); v<<c. Мы потребуем, чтобы в правой части (28) стояла обычная сила F, тогда: ▼ Компоненты четырех-вектора силы: 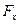 =Fx
=Fx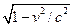 (29),
(29), 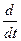
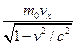 =
=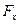 (30)-обыкновенные силы Ньютона.
(30)-обыкновенные силы Ньютона.
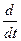
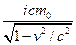 =Fτ uαvα=0, uα
=Fτ uαvα=0, uα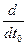 (m0 uα), воспользуемся (27): uαFα=0 (31).
(m0 uα), воспользуемся (27): uαFα=0 (31).
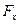
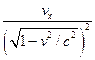 +
+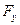
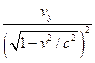 +
+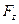
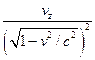 +
+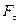
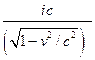 =0;
=0; 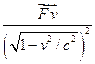 =-
=-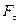
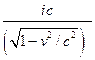 ;
; 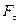
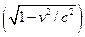 =(i/c)
=(i/c)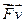 (32);
(32); 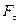 =
=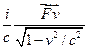 (33)
(33)
Тогда уравнение (27) четырех-вектора компоненты приобретают следующий вид: 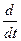
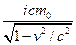 =
=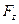
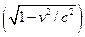 =
=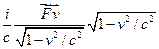 ;
; 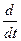
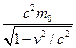 =
=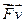 (34)
(34)
▼ Справа в (34) стоит мощность, следовательно, слева изменение энергии.
▼ Таким образом мы определяем полную энергию частицы. E=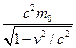 (35);
(35); 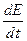 =
=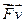 (36)
(36)
Проанализируем. Формула для трех-координат системы четырех-вектора (трехмерная формула для четырех-вектора): 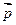 =
=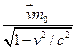 ;
; 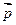 m(v)
m(v) (37); m(v)=
(37); m(v)=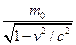 (38);
(38); 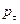 =
=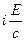 ; pα=(px, py, pz, i, E/c) (39).
; pα=(px, py, pz, i, E/c) (39).
E=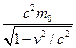
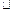
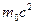 =
=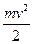 +…; E=
+…; E=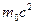 (40) для покоящегося тела. T=E-E0
(40) для покоящегося тела. T=E-E0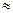 [m(0)-m0]c2
[m(0)-m0]c2
E=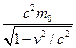 ;
; 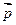 =
=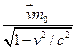 =>
=>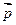 =
=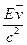 (41).
(41).
▼ (41) дает связь импульса частицы с энергией покоящейся частицы.
 2014-02-02
2014-02-02 197
197






