2014-02-02
503
Рис. 3.33.
Рис. 3.32.
Описание дискретно-непрерывных систем методом пространства состояний.
Рассмотрим описание в пространстве состояния следующей системы (рис. 3.32.)
 |
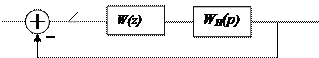Пусть непрерывная часть представлена передаточной функцией:
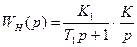
(3.42)
а дискретная часть – дискретной передаточной функцией:
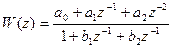(3.43)
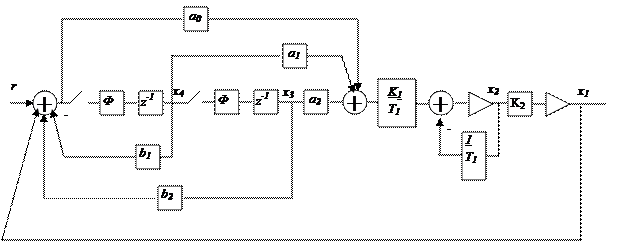
Схема переменных состояния имеет вид:
 |
-
-
При описании дискретно-непрерывных систем следует различать два момента:
· Описание системы в момент замыкания ключей (в этот момент срабатывает дискретная часть системы, непрерывная часть, являясь инерционной, не изменяется)
· Поведение системы в промежутке времени между замыканием ключей характеризуется изменением непрерывной части. Дискретная часть, благодаря фиксаторам, остается неизменной.
Чисто математически описание системы в момент замыкания ключей определяется матрицей B – матрицей ключей.
Описание системы в промежутке между замыканием ключей определяется матрицей А – матрицей коэффициентов.
Выбираем обобщенный вектор: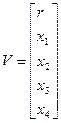
В момент замыкания ключей система описывается следующей системой:
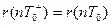
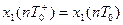
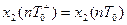(3.44)
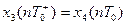
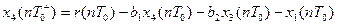
Матрица ключей имеет вид:
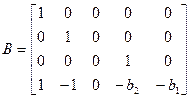
В векторно-матричном виде описание имеет вид:
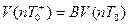(3.45)
В момент между замыканием ключей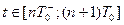 
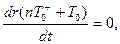
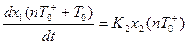
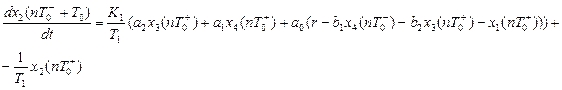
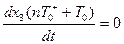(3.46)
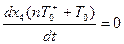
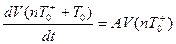
Как видно из описания переменные дискретной части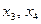 
остаются постоянными в течение всего времени 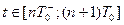, так как фиксаторы, работающие по принципу экстраполяторов нулевого порядка, сохраняют значение 
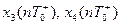постоянными в течение всего интервала квантования. Входная переменная 
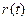обычно имеет вид ступенчатого сигнала, поэтому также остается постоянной. Изменяются переменные 
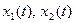, являющиеся переменными непрерывной части.
Описание в векторно-матричном виде:
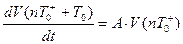(3.47)
или с использованием матрицы перехода:
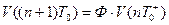(3.48)
Рассмотрим описание дискретно-непрерывной системы в течение интервала времени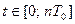 
.
В первый момент (момент замыкания ключей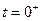 
) система описывается с помощью матрицы ключей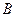 
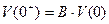. (49)
В момент между первым и вторым замыканием ключей, т. е. на интервале времени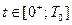 
поведение системы описывается с помощью матрицы перехода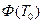 
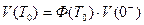(3.50)
или
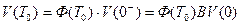(3.51)
Введем матрицу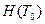 
- дискретную матрицу перехода. Тогда справедливо:
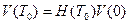(3.52)
В момент замыкания ключей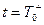 
система описывается:
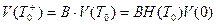(3.53)
В момент между вторым и третьим замыканием ключей, т. е. на интервале времени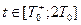 
поведение системы описывается:
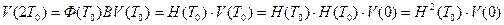(3.54)
Нетрудно заметить, что в момент времени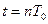 
поведение системы будет писываться следующим уравнением:
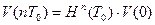(3.55)
Данное уравнение называется уравнением переходных состояний и позволяет на основе известных матриц ключей 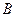и матрицы перехода 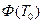в любой момент времени вычислить вектор состояния дискретно-непрерывной системы.
