2014-02-02
1150
Между матричными играми и линейным программированием существует взаимосвязь, состоящая в том, что, с одной стороны, решение любой матричной игры можно свести к решению пары двойственных друг другу задач линейного программирования специалыуэго вида, а с другой стороны, наоборот, любая задача линейного программирования, у которой существует решение, может быть сведена к матричной игре специального вида. Таким образом, в этом смысле теория линейного программирования эквивалентна теории матричных игр.
Сформулируем теорему, устанавливающую сведение решения любой матричной игры к решению пары двойственных задач линейного программирования специального вида. При этом будем предполагать, что все элементы матрицы игры
| 
| … | 
|
| 
| … | 
|
| … | … | … | … |
| 
| … | 
|
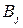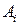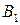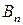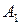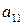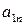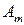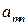положительны:
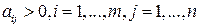(12.1)
Условие (12.1) не умаляет общности, поскольку матрица с любыми элементами может быть приведена к матрице с положительными элементами аффинным преобразованием
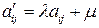
где
, по которому к каждому элементу исходной матрицы прибавляется достаточно большое положительное число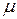 
, например, большее максимального модуля неположительных элементов матрицы; при этом оптимальные стратегии остаются прежними, а цена игры увеличивается на прибавленную константу .
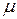Теорема 20.1. Решение матричной игры тхп с матрицей А, элементы которой удовлетворяют условию (12.1), эквивалентно решению следующей пары двойственных друг другу стандартных задач линейного программирования:
найти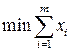 
, при ограничениях
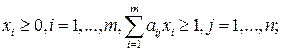(12.2)
найти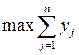 
при ограничениях
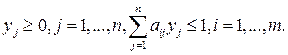(12.3)
Точнее говоря, если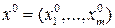 
- оптимальное решение задачи (12.2), 
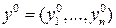- оптимальное решение задачи (20.3), то
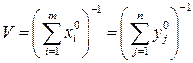(12.4)
- цена игры с матрицей А,
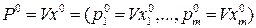(12.5)
- оптимальная стратегия игрока А,
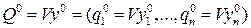
- оптимальная стратегия игрока В.
Пример. Необходимо найти решение матричной игры 3x3 с матрицей
| B A |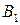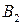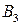
| 
| 
|
|
| |||
| |||
|
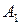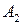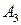Чтобы сделать все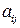 
неотрицательными, прибавим ко всем элементам матрицы 
. Получим матрицу:
| B A |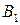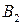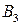
|
|
|
|
| |||
|
| |||
|
|
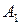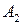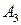При этой цена игры увеличится на 5, а решение не изменится.
Определим оптимальную стратегию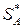 
. Условия (12.3) имеют вид:
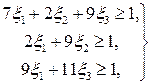(12.6)
где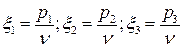 
Чтобы избавиться от знаков неравенства, введем фиктивные переменные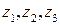
; условия (12.6) запишутся в виде:
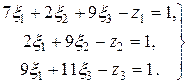(12.7)
Линейная форма Ф имеет вид:
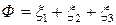
и должна быть сделана как можно меньше.
Если все три стратегии В являются «полезными», то все три фиктивные переменные 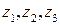обратятся в нуль (т. е. выигрыш, равный цене игры 
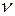, будет достигаться при каждой стратегии 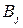). Но мы пока не имеем оснований утверждать, что все три стратегии являются «полезными». Чтобы проверить это. попытаемся выразить форму Ф через фиктивные переменные 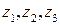и посмотрим, добьемся ли мы, полагая их рапными нулю, минимума формы. Для этого разрешим уравнения (5.7) относительно переменных 
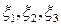(т. е. выразим 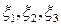через фиктивные переменные ):
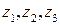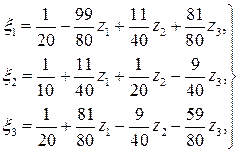(12.8)
Складывая 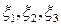получим:
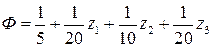(12.9)
В выражении (12.9) коэффициенты при всех 
положительны; значит, любое увеличение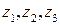сверх нуля может привести только к увеличению формы Ф, а мы хотим, чтобы она была минимальна. Следовательно, значениями 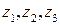обращающими форму (12.9) в минимум, являются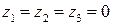 
Подставляя их в формулу (12.9), находим минимальное значение формы Ф: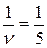 
,
откуда цена игры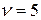 
.
Подставляя нулевые значения 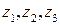в формулы (5.8), находим:
,
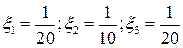или, умножая их на ,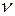
.
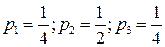Таким образом, оптимальная стратегия А найдена:
,
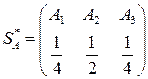т. е. мы должны в одной четверти всех случаев писать цифру 1, в половине случаев 2 и в остальной четверти случаев 3.
Зная цену игры 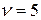, можно уже известными способами найти оптимальную стратегию противника
.
Для этого воспользуемся нашими любыми двумя «полезными» стратегиями (например, 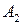и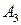) и напишем уравнения:
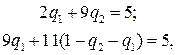
откуда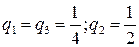 
.Оптимальная стратегия противника будет такой же, как наша:
.
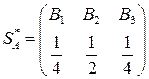Теперь вернемся к первоначальной (не преобразованной) игре. Для этого нужно только от цены игры 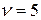отнять величину, прибавленную к элементам матрицы. Получим цену исходной игры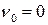 
. Следовательно, оптимальные стратегии обеих сторон обеспечивают средний выигрыш, равный нулю; игра в одинаковой мере выгодна или невыгодна для обеих сторон.
