Корабль в процессе плавания вовлекает окружающие массы воды в движение, благодаря которому происходит изменение существовавшего ранее поля давлений и скоростей.
Гидродинамическое поле корабля – это поле давлений и скоростей, создаваемых кораблем в окружающей его водной среде.
Гидродинамическое поле корабля используется со второй мировой войну для срабатывания неконтактных взрывателей донных мин.
О большом внимании зарубежных специалистов к этому полю говорит оснащение кораблей флотов НАТО и Японии гидродинамическими тралами.
При движении корабль вытесняет воду носом, которая затем по мере продвижения его вперед, подтекает к корме. Поэтому приближенно можно считать, что движение воды у носовой оконечности корабля такое, что если бы в носу был помещен точечный или сферический водяной источник. У кормовой же оконечности движение воды сходно с движением от размещенного в корме стока такой же, как у источника, интенсивности, равной 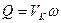 ,
, 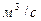 , где
, где 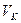 – скорость корабля,
– скорость корабля, 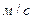 ;
; 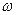 – площадь погруженной части мидель-шпангоута,
– площадь погруженной части мидель-шпангоута, 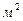 .
.
Для удобства анализа гидродинамического поля принимают следующую расчетную схему: считают, что корабль, представленный источником и стоком равной интенсивности, стоит на месте, а на него со скоростью, равной скорости корабля набегает вода. При этом параметры воды изменяются так же, как и при движении корабля.
Допустим, поток жидкости с равномерной скоростью 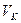 набегает на корабль, как показано на рис. 29.
набегает на корабль, как показано на рис. 29.
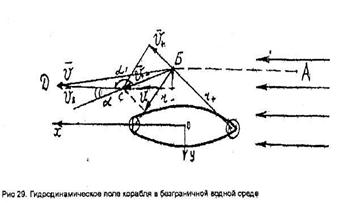
Направим ось 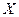 параллельно потоку, Возьмем две точки, лежащие на одном уровне: одна в невозмущенной части потока (вдали от корабля), а другая – в возмущенной части потоке (вблизи от корабля). Согласно уравнению Бернулли для точек
параллельно потоку, Возьмем две точки, лежащие на одном уровне: одна в невозмущенной части потока (вдали от корабля), а другая – в возмущенной части потоке (вблизи от корабля). Согласно уравнению Бернулли для точек 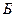 и
и 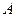 имеем:
имеем:
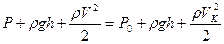
тогда
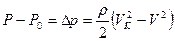 (*)
(*)
Скорость движения жидкости в возмущенной части потока равна сумме скоростей набегающего потока и индуктированной кораблем. Индуктированные скорости жидкости в точке 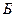 будут равны:
будут равны:
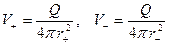
где 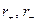 – расстояния от источника и стока до данной точки.
– расстояния от источника и стока до данной точки.
Тогда полная скорость в точке 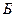 будет равна:
будет равна:
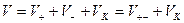
Обозначим угол  через
через 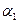 , тогда по теореме косинусов имеем для треугольника
, тогда по теореме косинусов имеем для треугольника 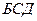 :
:
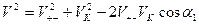
Или, перейдя к углу 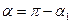 , можно записать:
, можно записать:
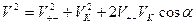
Поскольку 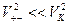 , то членом
, то членом 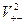 в уравнении можно пренебречь, тогда:
в уравнении можно пренебречь, тогда:
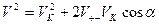
Подставив в выражение (*) значение 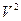 , имеем:
, имеем:

Величина 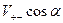 – есть проекция вектора скорости
– есть проекция вектора скорости 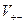 на ось
на ось 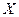 . Обозначив ее
. Обозначив ее 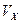 , получим:
, получим:
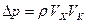
Таким образом, величина гидродинамического давления зависит от скорости корабля и от величины индуцированной скорости, которая определяется водоизмещением корабля и формой его обводов.
Если точка  расположена между оконечностями корабля, то угол
расположена между оконечностями корабля, то угол  будет больше
будет больше  , но меньше
, но меньше 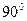 , поэтому
, поэтому 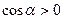 и
и 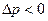 , т.е. под кораблем находится зона разряжения. Примерно под оконечностями корабля
, т.е. под кораблем находится зона разряжения. Примерно под оконечностями корабля 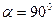 , тогда
, тогда 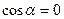 и
и 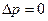 . Очевидно, что и вдали от корабля
. Очевидно, что и вдали от корабля 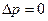 . Но, если точка
. Но, если точка 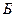 находится перед кораблем или позади него, то
находится перед кораблем или позади него, то 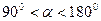 ,
, 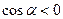 и
и 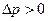 , т. е. перед кораблем и позади него на не очень больших расстояниях находятся зоны повышенных давлений (рис. 30).
, т. е. перед кораблем и позади него на не очень больших расстояниях находятся зоны повышенных давлений (рис. 30).
Зона пониженного давления, находящаяся под кораблем, используется для срабатывания гидродинамических неконтактных взрывателей.
 2014-02-02
2014-02-02 1758
1758








