2014-02-02
7964Лекция 6. Канонические формы логических формул, используемых в ЭВМ
Вопросы:
6.1 Основные термины. Понятие СДНФ и СКНФ.
6.2 Алгоритмы построения СДНФ и СКНФ по таблице истинности.
Всякая логическая формула определяет некоторую булевую функцию. В то же время ясно, что для всякой булевой функции можно записать бесконечно много формул ее представляющих (см. задание 3 к § 3.6). Действительно, если имеется хотя бы одна формула, выражающая булеву функцию, то, используя тождественные преобразования, можно изменить эту формулу, построив сколь угодно сложную равносильную формулу, например,
a xor b ≡ (a and (not b)) or ((not a) and b).
Одна из основных задач алгебры логики — нахождение канонических форм (т. е. формул, построенных по определенному правилу, канону), а также наиболее простых формул, представляющих булевы функции.
Определение 1. Если логическая функция выражена через дизъюнкцию, конъюнкцию и отрицание переменных, то такая форма представления называется нормальной.
Среди нормальных форм выделяют такие, в которых функции записываются единственным образом. Их называют совершенными.
Особую роль в алгебре логики играют классы совершенных дизъюнктивных и конъюнктивных нормальных форм (СДНФ и СКНФ). В их основе лежат понятия элементарной дизъюнкции и элементарной конъюнкции.
Определение 2. Формулу называют элементарной конъюнкцией, если она является конъюнкцией одной или нескольких переменных, взятых с отрицанием или без отрицания. Одну переменную или ее отрицание считают одночленной элементарной конъюнкцией.
Пример 1. Формулы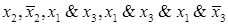 
являются элементарными конъюнкциями; первые две из них — одночленными.
Определение 3. Формула называется дизъюнктивной нормальной формой (ДНФ), если она является дизъюнкцией неповторяющихся элементарных конъюнкций. ДНФ записываются в виде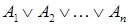 
, где каждое Ai — элементарная конъюнкция.
Пример 2. Приведем две дизъюнктивные нормальные формы: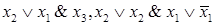 
Определение 4. Формула А от k переменных называется совершенной дизъюнктивной нормальной формой (СДНФ), если:
1) А является ДНФ, в которой каждая элементарная конъюнкция есть конъюнкция k переменных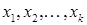 
, причем на i -м месте этой конъюнкции стоит либо переменная 
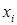, либо ее отрицание;
2) все элементарные конъюнкции в такой ДНФ попарно различны.
Задание 1. Даны формулы:
;
;
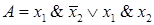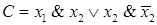
Определить, являются ли они СДНФ двух переменных.
Решение. Формула А является СДНФ двух переменных. Формулы В и С не являются СДНФ. Формула В зависит от трех переменных, но количество переменных в элементарных конъюнкциях меньше трех. В формуле С переменная х2 дважды входит в одну и ту же элементарную конъюнкцию.
Совершенная дизъюнктивная нормальная форма представляет собой формулу, построенную по строго определенным правилам с точностью до порядка следования элементарных конъюнкций (дизъюнктивных членов) в ней. Она является примером однозначного представления булевой функции в виде формульной (алгебраической) записи.
Определение 5. Формула называется элементарной дизъюнкцией, если она является дизъюнкцией (быть может, одночленной) переменных и отрицаний переменных.
Пример 1 Приведем три элементарные дизъюнкции:
.
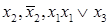Определение 6. Формула называется конъюнктивной нормальной формой (КНФ), если она является конъюнкцией неповторяющихся элементарных дизъюнкций.
КНФ записываются в виде 
, где каждое Ai — элементарная дизъюнкция.
Пример 2. Формулы
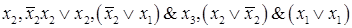
являются конъюнктивными нормальными формами.
Определение 7. Формула А от k переменных называется совершенной конъюнктивной нормальной формой (СКНФ),если:
1) А является КНФ, в которой каждая элементарная дизъюнкция есть дизъюнкция k переменных 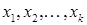, причем на i -м месте этой дизъюнкции стоит либо переменная х, либо ее отрицание;
2) все элементарные дизъюнкции в такой КНФ попарно различны.
Задание 2. Даны формулы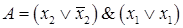 
и 
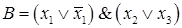. Определить, являются ли они СКНФ.
Решение. Формула А является СКНФ, а формула В не является СКНФ, поскольку переменная 
дважды входит в первый конъюнктивный член, кроме того, количество переменных в каждой элементарной дизъюнкции меньше трех, в то время как формула зависит от трех переменных.
Вопрос. Всякую ли логическую функцию можно представить в одной из рассмотренных канонических совершенных форм?
Ответ. Да, любую булеву функцию, не равную тождественно 0 или 1, можно представить в виде СДНФ или СКНФ.
Для обоснования этого утверждения имеется теорема.
Теорема 1. Пусть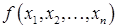 
— булева функция от n переменных, не равная тождественно нулю. Тогда существует совершенная дизъюнктивная нормальная форма, выражающая функцию f.
Алгоритм построения СДНФ по таблице истинности:
1. В таблице истинности отмечаем наборы переменных, на которых значение функции f равно единице.
2. Записываем для каждого отмеченного набора конъюнкцию всех переменных следующим образом: если значение некоторой переменной в этом наборе равно 1, то в конъюнкцию включаем саму переменную, в противном случае — ее отрицание.
3. Все полученные конъюнкции связываем операциями дизъюнкции.
Следствие теоремы 1. Для любой формулы можно найти равносильную ей ДНФ.
Пример 3. Требуется построить формулу для функции f (x1, х2, х3), заданной таблицей истинности:
| x1 | x2 | x3 | f(x1, х2, х3) |
Используя описанный выше алгоритм, построим для нее СДНФ:
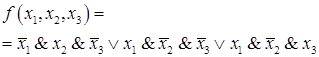
Теорема 2. Пусть 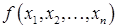— булева функция n переменных, не равная тождественно единице. Тогда существует совершенная конъюнктивная нормальная форма, выражающая функцию f.
На основании теоремы 2 можно предложить следующий алгоритм построения СКНФ по таблице истинности функции.
Алгоритм построения СКНФ по таблице истинности^
1. В таблице истинности отмечаем наборы переменных, на которых значение функции f равно нулю.
2. Записываем для каждого отмеченного набора дизъюнкцию всех переменных следующим образом: если значение некоторой переменной в этом наборе равно 0, то в конъюнкцию включаем саму переменную, в противном случае — ее отрицание.
3. Все полученные дизъюнкции связываем операциями конъюнкции.
Следствие теоремы 2. Для любой формулы можно найти равносильную ей КНФ.
Пример 4. Выразим функцию импликация с помощью операций отрицания, дизъюнкции и конъюнкции. Для этого запишем таблицу истинности функции импликация:
| x1 | x2 | f(x1, х2, х3) |
Так как в таблице истинности только один набор переменных, на котором функция принимает значение 0, то СКНФ принимает вид:
Ответ: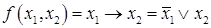 
Вывод: Из алгоритмов построения СДНФ и СКНФ следует, что если на большей части наборов значений переменных функция равна 0, то для получения ее формулы проще построить СДНФ, в противном случае — СКНФ.
