Системы оптимального быстродействия

Лекция 13.

Рассмотрим в качестве типовой практически часто встречаю­щуюся задачу управления, оптимального по быстродействию.

В линейной САУ быстродействие может быть сделано сколь угодно большим путем введения соответствующей коррекции. Например, при рассмотрении темы о последовательных корректирующих звеньях в линейных САУ, в случае апериодического звена с передаточной функцией включение перед ним пропорционально-дифференцирующего звена позволяет полностью скомпенсировать инерционность основного звена и получить бесконечно большое быстродействие, т. е. идеальное звено с t _п = 0.

Однако реальные САУ нелинейны - в них всегда существуют ограничения переменных величин и их производных. Если же в САУ ограничена хотя бы одна переменная, это ограничи­вает и время переходных процессов в ней. В частности, упомянутая выше полная компенсация инерционности апериодического звена первого порядка путем введения дополнительного воздействия по производной в этом случае практически не реализуема, так как при скачкообразном изменении входного сигнала сигнал по его производной будет бесконечно велик и, следовательно, не может быть пропущен звеном без искажения вследствие ограничения (насыщения) его статической характеристики. Например, если этим звеном является электрический двигатель постоянного тока, его выходной величиной - скорость, а входной - напряжение якоря, то из-за ограничения величины этого напряжения макси­мально допустимым значением (по условию электрической проч­ности изоляции и механической целостности якоря при действии центробежных сил) время переходного процесса изменения ско­рости от одного ее значения до другого тоже получается ограни­ченным.

Начнем рассмотрение задачи оптимального по быстродействию управления с простейшего случая, когда внешнее воздействие, вызывающее переходный процесс, представляет собой ступеньку, т. е. постоянно в течение переходного процесса. Пусть объект управления является линейным апериодическим звеном первого порядка (рис.13.1, а), а входной управляющий сигнал U ограни­чен по величине некоторым предельным значением U _пр. (Этим звеном может быть, например, двигатель постоянного тока, у которого вход - напряжение, ограниченное определенным пределом, а выход - скорость вращения вала.) Рассмотрим вопрос, каким образом следует изменять управляющий сигнал U, чтобы обеспечить максимально быстрое изменение сигнала Х, скажем, от нуля до определенного значения Х _ст. (В случае двига­теля, таким образом, речь идет о максимально быстром его разгоне до определенной скорости).

Оптимальный процесс управления показан на рис. 13.1, б. Для обеспечения возможно быстрого изменения Х необходимо, очевидно, сигнал U мгновенно изменить до предельно допустимого значения U _пр. и удерживать это значение до тех пор, пока Х не достигнет заданного значения Х _ст. При этом Х будет изменяться с максимально возможной, с учетом ограничения U,быстротой. После этого U следует мгновенно уменьшить до значения, соот­ветствующего по статической характеристике Х = Х _ст., т. е. до U _ст. = Х _ст. / k. На этом переходный процесс заканчивается. Его длительность t _п определяется инерционностью звена, т. е. постоянной времени Т,величиной ограничения U _пр.и, конечно, заданными начальным и конечным значениями Х. При этом, чем больше U _пр.,тем меньше t _п:при U _пр. 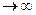время t _п 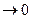. (Последний предел как раз и получается при компенсации инерционности линейного звена введением дополнительного воздействия по производной).

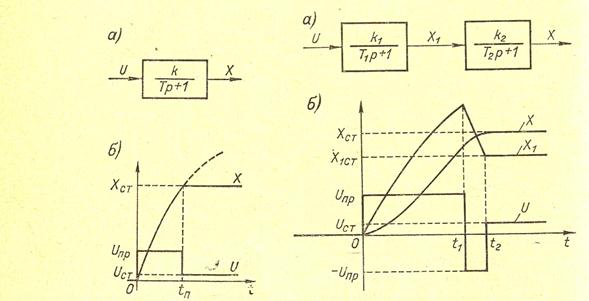
Рис.13.1. Пример оптимального по Рис. 13.2. Пример оптимального по быстродействию

быстродействию управления объек- управления объектом второго порядка.

том первого порядка.

Пусть теперь имеем линейный объект второго порядка, например, в виде двух последовательно соединенных апериодических звеньев первого порядка (рис. 13,2, а)при наличии по-прежнему ограничения U. (Это может быть тоже задача разгона двигателя, но описываемого уравнением второго порядка.) Оптимальный переходный процесс показан на рис. 13,2, б. Так как сигнал U ограничен, то ограниченным является и сигнал Х ₁ на входе второго звена. Его предельное значение Х _1пр.= kU _пр.Очевидно, в этом случае входной сигнал U следует изменять так, чтобы сигнал Х ₁ на входе второго звена был предельно близок по форме оптимальному управляющему сигналу для звена первого порядка, показанному на рис. 13.1, б. Для этого сигнал U на входе первого звена вначале мгновенно доводится до своего предельного значения U _пр., что обеспечивает максимально быстрый рост Х ₁ в сторону его предельного значения. Затем для возможно быстрого сброса сигнала Х ₁ до его значения Х _1ст., соответствующего требуемому значению Х _ст., управляющий сигнал U мгновенно переключается с + U _пр. на - U _пр. и сохраняет это значение до тех пор, пока Х ₁ не снизится до величины Х _1ст.. В этот момент U мгновенно дово­дится до значения 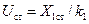, на чем процесс управления заканчивается. Из-за наличия первого инерционного звена фронт и спад импульса Х ₁ на входе второго звена получаются не верти­кальными, как на рис. 13.1, б. Соответственно и длительность переходного процесса оказывается больше.

Итак, для двух звеньев первого порядка процесс управления состоит из двух интервалов: в первом U = + U _пр., а во втором U = - U _пр..

В общем случае для п последовательно соединенных линейных звеньев первого порядка или, что то же самое, для линейного объекта n-го порядка с действительными отрицательными корнями характеристического урав­нения оnтиммьное уnравленuе nри налuчuu огранuченuя управляющего сигнала состоит uз n uнтервалов, в каждом из которых этот сигнал nринимает свое nредельное значенuе, т. е. уnравленuе является релейным. В конце каждого uнтервала nроисходит uзмене­ние знака управляющего сигнала.

СИСТЕМЫ ТЕЛЕМЕХАНИКИ.