Если А есть В, то С есть К

М есть Р

К есть М

К есть Р.

«М есть Р» называется большей посылкой, «К есть М» называется меньшей посылкой, а «К есть Р» называется выводом.

Встречаются также условные силлогизмы, т.е. силлогизмы которые строятся по схеме

А есть В

С есть К.

Покажем на примерах как в доказательствах можно явно выделять силлогизмы.

ТЕОРЕМА. Если в четырехугольнике противоположные стороны попарно равны, то такой четырехугольник является параллелограммом.

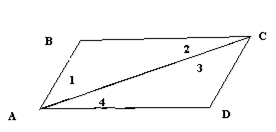
Доказательство. Проведем диагональ АС.

1-й силлогизм.

(Большая посылка) Если три стороны одного треугольника соответственно равны трем сторонам второго треугольника, то такие треугольники равны.

(Меньшая посылка) АС - общая сторона треугольников АВС и СДА; АВ=СД, ВС=ДА (по условию).

(Вывод) DАВС=DСДА.

2-й силлогизм.

(Б.п.) В равных треугольниках равны соответствующие углы.

(М.п.) Ð1 и Ð3 - соответствующие; Ð2 и Ð4 - соответствующие в равных треугольниках АВС и СДА.

(Вывод) Ð1 = Ð3, Ð2 = Ð4.

3-й силлогизм.

(Б.п.) Если при пересечении двух прямых третьей внутренние накрест лежащие углы равны, то эти две прямые параллельны.

(М.п.) Ð1 и Ð3 - равные и накрест лежащие при прямых АВ и СД, пересеченных прямой АС; Ð2 и Ð4 равные и накрест лежащие при прямых СВ и АД, пересеченных прямой АС.

(Вывод) АВêêСД и ВСêêАД.

4-й силлогизм.

(Б.п.) Четырехугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом.

(М.п.) В четырехугольнике АВСД АВêêСД и ВСêêАД.

(Вывод) АВСД - параллелограмм.

Упражнение. Проведите доказательство следующей теоремы с использованием силлогизмов. В равнобедренном треугольнике углы при основании равны.

В качестве большей посылки силлогизма могут выступать ранее доказанные теоремы их следствия, аксиомы, а также определения. Меньшая посылка может включать в себя часть условия доказываемой теоремы или следствие, полученное из условия в предшествующих силлогизмах этого же доказательства.

В школьных учебниках по математике доказательства теорем не разбиты на силлогизмы. Учителю по возможности необходимо проводить работу со школьниками, направленную на преобразование книжных доказательств. Такая работа будет способствовать эффективному повторению, глубокому и прочному усвоению учебного материала, а также развитию творческого мышления.

В основе метода математической индукции лежит аксиома индукции - одна из аксиом натуральных чисел.

Данный метод формулируется следующим образом:

Если некоторое предложение Р(к), зависящее от натурального переменного числа к,

1) верно при к = 1,

2) из того, что оно верно при к = n, следует, что оно верно и при следующем к = n + 1,

то предложение Р(к) верно для любого натурального числа к.

Доказательство методом математической индукции обязательно должно содержать две части:

а) проверку истинности предложения Р(1);

б) доказательство импликации Р(к)ÞР(к+1).

По ныне действующей программе метод математической индукции изучается в классах с углубленным изучением математики (либо в 8-м, либо в 10-м). Этот метод является трудным и непривычным даже для старшеклассников, а потому его усвоению необходимо уделить достаточно внимания путем разбора и решения большого количества разнообразных задач и разъяснением необходимости именно одновременного выполнения пунктов а) и б).

Для этого необходимо рассмотреть ряд примеров, когда индукция является неполной. Например, формула ¦(к) = 2к² + 29 дает 28 простых чисел при первых 28 значениях к. Здесь пункт а) выполнен, а вот пункт б) не справедлив, так как уже при к = 29 получаем составное число 29×59.

Метод математической индукции широко применяется как в алгебре, так и в геометрии. В алгебре он используется для доказательства

1) равенств;

2) неравенств;

3) делимости чисел;

4) различных формул.

Рассмотрим примеры для каждого из этих случаев.

ПРИМЕР 1. Докажите, что

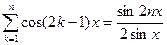(1)

Доказательство. Проверим наше равенство при n=1. Имеем

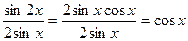Получаем, что при n=1 равенство (1) верно.

Предположим, что (1) верно при n=k и докажем его при n = k + 1.

Имеем

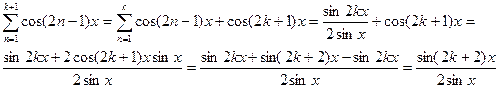
Используя метод математической индукции, получаем, что равенство (1) верно для всех натуральных n.

ПРИМЕР 2. Пусть х₁, х₂, …, х_n - произвольные положительные числа, причем х₁х₂×××х_n=1. Доказать, что

х₁+х₂+…+х_n³n.

Доказательство. Если n=1, то по условию х₁=1 и, следовательно, можно написать х₁³1, т.е. для n=1 неравенство верно.

Предположим, что для n=k утверждение верно. Пусть х₁, х₂, …, х_k, х_k₊₁ - произвольные положительные числа и х₁х₂×××х_kx_k₊₁=1. Могут представиться два случая: либо все эти числа равны 1, и тогда их сумма равна k+1, либо среди этих чисел есть хотя бы одно число, не равное 1, и тогда обязательно есть, по крайней мере, еще одно число, не равное 1, причем, если одно из них меньше 1, то второе обязательно больше 1. Не ограничивая общности, можно считать, что x_k>1, а x_k₊₁<1. Рассмотрим теперь к чисел