Для дискретной случайной величины.
Пусть 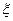 — дискретная случайная величина, принимающая значения
— дискретная случайная величина, принимающая значения 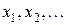 , причем
, причем 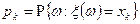 . Математическим ожиданием дискретной случайной величины
. Математическим ожиданием дискретной случайной величины 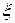 называется величина
называется величина
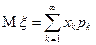 ,
,
если ряд справа сходится абсолютно.
Пусть 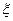 — абсолютно непрерывная случайная величина с плотность распределения
— абсолютно непрерывная случайная величина с плотность распределения 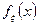 Математическим ожиданием абсолютно непрерывной случайной величины
Математическим ожиданием абсолютно непрерывной случайной величины 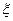 называется величина
называется величина
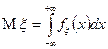 ,
,
если интеграл сходится абсолютно.
Определение. Дисперсией случайной величины 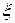 называется
называется 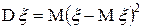 .
.
Определение. Для целого неотрицательного 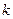 начальным моментом порядка k называется величина
начальным моментом порядка k называется величина 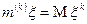 .
.
Определение. Для целого неотрицательного 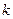 центральным моментом порядка k называется величина
центральным моментом порядка k называется величина 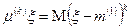 .
.
7. Числовые характеристики системы случайных величин.
| Определение | Ковариацией двух случайных величин 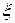 и и 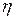 называется величина: называется величина:
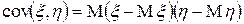 .
Ковариацию также называют вторым смешанным центральным моментом случайных величин .
Ковариацию также называют вторым смешанным центральным моментом случайных величин 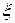 и и 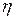 . .
|
Из свойств математического ожидания непосредственно вытекают свойства ковариации:
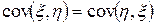 (симметричность);
(симметричность);
2. 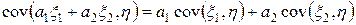 (линейность).
(линейность).
| Определение | Коэффициентом корреляции двух случайных величин 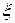 и и 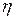 называется величина: называется величина:
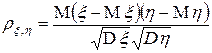 . .
|
| Определение | Ковариационной матрицей системы случайных величин 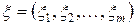 называется матрица называется матрица 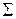 , элементами которой являются ковариации , элементами которой являются ковариации 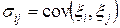 . .
|
| Определение | Корреляционной матрицей системы случайных величин 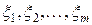 называется матрица называется матрица 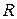 , элементами которой являются коэффициенты корреляции , элементами которой являются коэффициенты корреляции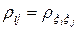 . .
|
 2014-02-18
2014-02-18 270
270






