План
Примерный план лекции №3 и основные определения.
Темы: Теория поведения потребителя: задача потребителя; случай натурального дохода; экономика обмена (начало)
- Задача потребителя: характеристика решения и примеры поиска функций спроса.
- Бюджетное ограничение и задача потребителя в случае натурального дохода.
- Экономика обмена: допустимые распределения, ящик Эджворта.
1. Задача потребителя:
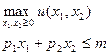
Решение задачи потребителя 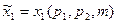 ,
, 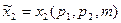 - функции (обычного или маршаллианского) спроса.
- функции (обычного или маршаллианского) спроса.
Функции спроса однородны нулевой степени по ценам и доходу, т.е. 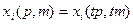 для любого
для любого 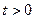 .
.
Если максимизируя свою полезность на бюджетном множестве потребитель выбирает набор с положительным количеством обоих благ (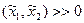 - внутреннее решение), то
- внутреннее решение), то 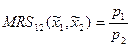 .
.
Если, максимизируя свою полезность на бюджетном множестве, потребитель приобретает положительное количество блага 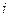 , то для блага
, то для блага 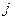 выполнено:
выполнено:
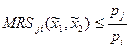 .
.
Функции спроса для функции полезности Кобба-Дугласа 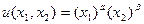 , где
, где 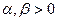 :
: 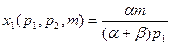 ,
, 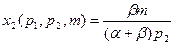 .
.
Функции спроса для квазилинейной функции полезности вида 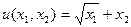 :
:
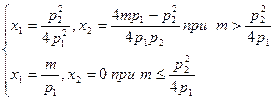
Задача потребителя и ее решение с помощью условий Куна-Таккера для функции полезности 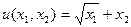 .
.
Задача потребителя:
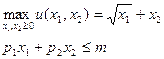 :
:
Пусть 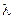 – множитель Лагранжа, тогда условия Куна-Таккера для этой задачи имеют вид:
– множитель Лагранжа, тогда условия Куна-Таккера для этой задачи имеют вид:
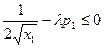 и
и 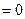 , если
, если 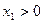 (1)
(1)
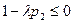 и
и 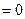 , если
, если 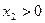 (2)
(2)
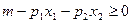 и
и 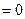 , если
, если 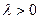 (3)
(3)
Заметим, что, во-первых, т.к. предпочтения потребителя строго монотонны, то на решении задачи бюджетное ограничение будет выполняться как равенство (поэтому условие (3) выполняется как равенство), во-вторых, т.к. доход потребителя по предположению положителен, 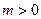 , то оптимальным не может быть набор, в котором отсутствует оба блага; в-третьих, поскольку функция полезности строго вогнута (а, следовательно, предпочтения строго выпуклы), то условия первого порядка являются необходимыми и достаточными.
, то оптимальным не может быть набор, в котором отсутствует оба блага; в-третьих, поскольку функция полезности строго вогнута (а, следовательно, предпочтения строго выпуклы), то условия первого порядка являются необходимыми и достаточными.
Заметим, что 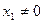 , поэтому условие (1)
, поэтому условие (1) 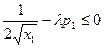 всегда выполняется как равенство. Т.к. из условия (2) следует, что
всегда выполняется как равенство. Т.к. из условия (2) следует, что 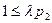 , то
, то 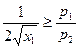 , причем
, причем 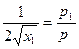 если
если 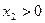 . Таким образом,
. Таким образом, 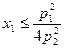 , и
, и 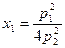 , если
, если 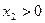 .
.
С другой стороны расходы на приобретение блага 1, 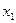 ,не превосходят доход:
,не превосходят доход: 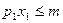 , то есть
, то есть 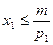 , причем
, причем 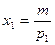 , если
, если 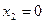 .
.
Поэтому 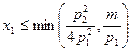 . Покажем, что
. Покажем, что 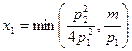 . Действительно, если
. Действительно, если 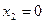 , то
, то 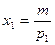 , а если
, а если 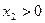 , то
, то 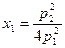 .
.
Поскольку 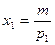 Û
Û 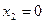 , то
, то 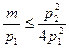 Û
Û 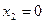 . Таким образом,
. Таким образом, 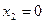 Û
Û 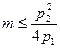 . В итоге получаем приведенные выше функции спроса.
. В итоге получаем приведенные выше функции спроса.
2. Поведение потребителя в случае натурального дохода. Предположим, что индивид обладает некоторым запасом благ 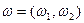 , которые предлагаются на рынке по ценам
, которые предлагаются на рынке по ценам 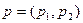 , и не имеет фиксированного дохода, тогда бюджетное ограничение потребителя имеет вид:
, и не имеет фиксированного дохода, тогда бюджетное ограничение потребителя имеет вид: 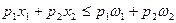 . Графически, бюджетная линия проходит через точку первоначального запаса точка
. Графически, бюджетная линия проходит через точку первоначального запаса точка 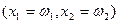 и имеет наклон
и имеет наклон 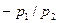 . Решение задачи потребителя, набор
. Решение задачи потребителя, набор 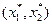 , теперь зависит как от цен, так и от первоначального запаса благ:
, теперь зависит как от цен, так и от первоначального запаса благ: 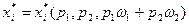 .
.
Если 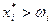 , то говорят, что потребитель является чистым покупателем или чистым потребителем данного блага.
, то говорят, что потребитель является чистым покупателем или чистым потребителем данного блага.
Если 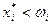 , то говорят, что потребитель является чистым продавцом или чистым поставщиком данного блага.
, то говорят, что потребитель является чистым продавцом или чистым поставщиком данного блага.
В экономике с двумя благами при положительных ценах потребитель не может быть чистым покупателем или чистым продавцом обоих благ одновременно.
3. Экономика обмена. Обозначим через 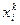 потребление блага
потребление блага 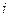 ,
, 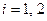 потребителем
потребителем 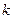 ,
, 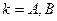 , а через
, а через 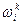 - первоначальный запас блага
- первоначальный запас блага 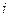 у потребителя
у потребителя 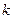 .
.
Распределением называется пара потребительских наборов 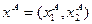 и
и 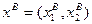 , т.е.
, т.е. 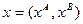 .
.
Распределение называется допустимым, если потребляемое количество каждого блага равно совокупному запасу этого блага, т.е. 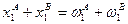 и
и 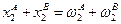 .
.
Допустимое распределение 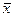 называется Парето-оптимальным (эффективным), если нельзя улучшить положение одного потребителя, не ухудшая положение другого. Другими словами, распределение
называется Парето-оптимальным (эффективным), если нельзя улучшить положение одного потребителя, не ухудшая положение другого. Другими словами, распределение 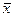 Парето-оптимально, если для него нельзя построить Парето-улучшение, т.е. не существует другого допустимого распределения
Парето-оптимально, если для него нельзя построить Парето-улучшение, т.е. не существует другого допустимого распределения 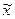 такого, что
такого, что 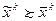 для всех потребителей и хотя бы для одного потребителя
для всех потребителей и хотя бы для одного потребителя 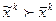 .
.
 2014-02-18
2014-02-18 247
247






