Основы теории погрешностей
Важнейшей характеристикой любого измерительного преобразователя является функция преобразования (см. (6) лекции 2).
Так как значения 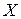 наносятся на шкалу прибора, то функцию преобразования еще называют градуировочной характеристикой. Для получения на выходе измерительного прибора значения измеряемой величины, нужно провести обратное преобразование:
наносятся на шкалу прибора, то функцию преобразования еще называют градуировочной характеристикой. Для получения на выходе измерительного прибора значения измеряемой величины, нужно провести обратное преобразование:
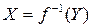 (11)
(11)
За счет помех и нестабильности на практике функция преобразования 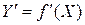 немного отличается от теоретической функции преобразования (6) в лекции 2. Отсюда следует, что измеренная величина
немного отличается от теоретической функции преобразования (6) в лекции 2. Отсюда следует, что измеренная величина 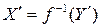 , полученная при обратном преобразовании будет отличаться от истинного значения измеряемой величины
, полученная при обратном преобразовании будет отличаться от истинного значения измеряемой величины 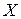 . Разность результата измерения
. Разность результата измерения 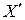 и истинного значения
и истинного значения 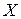 измеряемой величины, называется абсолютной погрешностью:
измеряемой величины, называется абсолютной погрешностью:
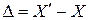 (12)
(12)
Условием достоверности проведенного измерения является неравенство 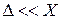 . Однако в связи с тем, что истинное значение измеряемой величины измерить невозможно, на практике абсолютную погрешность определяют как:
. Однако в связи с тем, что истинное значение измеряемой величины измерить невозможно, на практике абсолютную погрешность определяют как:
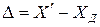 , (13)
, (13)
где 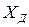 — это действительное значение величины, которое несколько отличается от истинного значения (
— это действительное значение величины, которое несколько отличается от истинного значения (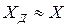 ), но его погрешность намного меньше, чем погрешность измеренного значения
), но его погрешность намного меньше, чем погрешность измеренного значения 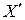 .
.
Абсолютная погрешность не может характеризовать точность выполняемых измерений. Числовой характеристикой точности измерения является относительная погрешность 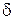 :
:
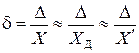 , (14)
, (14)
т. е. отношение абсолютной погрешности к значению измеряемой величины. Относительная погрешность может записываться в виде безразмерной десятичной дроби, либо выражаться в процентах.
Из (13) и (14) следует, что величина погрешности определяется приближенно. При этом точность нахождения погрешности обычно существенно меньше точности измеряемой величины, поскольку отношение 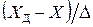 обычно больше
обычно больше 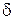 .
.
 2014-02-18
2014-02-18 1376
1376
