Рассмотрим погрешность, которая представляет собой функцию нескольких аргументов, из которых лишь один является случайной величиной. Такую погрешность иногда называют квазислучайной. В частности к такому типу погрешностей относится часто встречающаяся в практике радиоэлектронных измерений погрешность вида
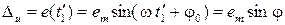 (19)
(19)
обусловленная действием синусоидальной помехи (наводки, пульсации)
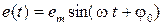 (20)
(20)
При этом параметр 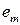 (амплитуда) в конкретных условиях остается неизменным, а параметр
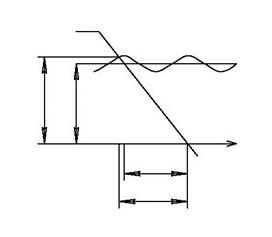
(амплитуда) в конкретных условиях остается неизменным, а параметр 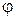 (фаза) — это случайная величина, все значения которой равновероятны (см. рис.3) и справедливо неравенство
(фаза) — это случайная величина, все значения которой равновероятны (см. рис.3) и справедливо неравенство 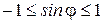 или
или
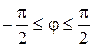 (21)
(21)
В этом интервале 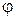 имеет равномерную плотность распределения, равную
имеет равномерную плотность распределения, равную 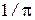 . Из теории вероятности известно, что если имеются
. Из теории вероятности известно, что если имеются 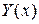 и
и 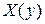 и они однозначны, и известно
и они однозначны, и известно 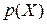 , а нужно определить
, а нужно определить 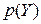 , то
, то
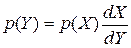 (22)
(22)
Используя выражение (22) найдем:
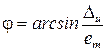 (22)
(22)
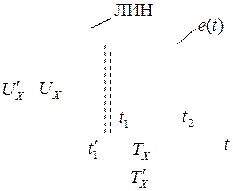
 | |||
 | |||
Возьмем производную:
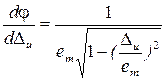 (23)
(23)
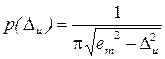 (24)
(24)
Выражение (24) определяет так называемое U – образное распределение погрешности, вызванное действием синусоидальной помехи. Такое распределение называется арксинусоидальным. Для него дисперсия
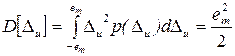 , (25)
, (25)
СКО: 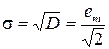 , (26)
, (26)
граничное значение 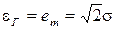 (27)
(27)
 2014-02-18
2014-02-18 613
613








